파력발전장치 주변 파동장 해석을 통한 파고계 적정 위치에 관한 고찰

1. 서 론

세계 각국은 지속가능하고 깨끗한 에너지원을 찾아 이를 공급하기 위해 신 재생에너지 개발에 박차를 가하고 있다. 특히, 파랑에너지는 에너지 밀도가 높은 것으로 알려져 많은 연구자들의 관심의 대상으로 떠오르고 있다(Drew et al.[2009]). 파랑에너지를 전기에너지로 변환하는 파력발전장치의 경우 상용화에 성공한 사례는 거의 없지만 최근 들어 유럽을 중심으로 상용화의 전 단계인 실해역 실증실험 건수가 증가하고 있어 가까운 장래에 파랑에너지로부터 안정적으로 전기를 공급 받을 수 있는 시대가 도래할 것으로 기대된다. 국내에서도 제주도 서쪽 차귀도 해역에 파력발전장치의 안전한 실증 및 성능평가를 위한 실해역 시험장이 완공되어 파력발전장치 개발을 위한 교두보가 마련되었다(Kim et al.[2016]).

파력발전장치의 효율은 입력인 파랑에너지 대비 출력인 전기에너지의 비로 정의된다. 따라서 파력발전장치의 성능을 정확히 평가하기 위해서는 파랑에너지에 대한 정확한 정보가 필요하다. 이를 위하여 실해역 시험장내에 파고계를 설치하여 장기간의 파랑 데이터를 수집한다. 연안에 입사하는 파랑은 수심 및 지형 변화에 의해 천수변형(Shoaling), 굴절(Refraction), 회절(Diffraction), 반사(Reflection), 쇄파(Wave breaking)등 복잡한 파랑변환 과정에 의해 파랑의 특성이 바뀌기 때문에 입사파의 측정은 가능한 한 파력발전장치와 가까운 위치에서 이뤄지는 것이 이상적이나 파력발전장치와의 충돌 위험과 함께 파력발전장치 주변에 형성되는 산란파와 방사파의 영향 등을 고려하여 적절한 위치를 선정하여야 한다. IEC(Internation Electrotechnical Commission) TS 62600-100에 따르면 파력발전장치내의 순수한 입사파 정보를 얻기 위해서는 파랑전달모델(Wave spatial transfer model)을 사용하여 파력발전장치에 의한 간섭 영향이 적은 위치로 정해야 하며 평균 산란파/방사파의 에너지가 최소 90% 이상 감소된 곳을 파고계 설치 위치로 권장하고 있다(IEC[2012]). IEC 규정 외에 파고계 적정 위치에 관한 다른 문헌들을 찾을 수가 없었다.

해양구조물 설계에 있어 파랑과 구조물간의 상호작용을 고려한 파동장 해석은 구조물에 가해지는 파력을 계산하거나 방파제, 이안제, 잠제 등과 같이 파랑제어를 목적으로 한 파의 회절과 산란 문제를 주로 다루었다(Penney et al.[1952]; Wiegel[1962]; Pos and Kilner[1987]; Lee et al.[2005]; Suh and Kim[2008]). 최근에는 대형 지지구조물에 다수의 파력발전장치를 배치하는 경우, 다수 구조물간의 상호작용을 고려하는 파동장 해석 연구가 수행되었다. Kim and Bae[2019]는 부유식 플랫폼내에 24개의 파력발전장치의 최적 배치를 위하여 지지 플랫폼과 24개의 파력발전장치간의 상호 간섭효과를 고려한 파동장 해석을 수행하였고, 지지 플랫폼내에 최대 파고가 형성되는 지점에 파력발전장치를 배치하여 추출 효율을 향상시켰다. Kim and Cho[2019]는 ‘Y’ 자형 수로형 공명구조물을 제안하고 수로내 유체공진에 의해 증폭되는 수면운동 특성을 파동장 해석을 통하여 살펴보았고, 수로내 정지파(Standing wave)의 최대 파고가 형성되는 역절점(Anti-node)에 파력발전장치를 배치하였을 때 파랑에너지의 출력 효율을 높일 수 있음을 보였다.

본 연구에서는 파력발전장치내에 입사하는 순수한 입사파를 계측하기 위한 파고계의 적절한 설치 위치를 조사하였다. 이를 위하여 고정식과 부유식 파력발전장치에 대하여 규칙파와 불규칙파 조건에서 입사파의 파향과 파고 그리고 주기를 바꿔가면서 파동장 해석을 수행하였다. 고정식 파력발전장치 주변 파동장 해석을 위한 계산 모델로 현재 제주도 실해역 시험장 1번 정박지에 설치된 용수 파력발전장치를 선정하였고, 부유식 파력발전장치에 대한 해석모델로 원기둥형과 사각형 파력발전장치를 살펴보았다. 파동장 해석은 포텐셜 이론에 기반을 둔 SeaFEM 상용 코드를 사용하였다. 이때 선형 해석과 함께 비선형 해석을 병행하여 비선형 효과의 영향을 분석하였다. 파고계의 유효 설치 영역을 나타내기 위해 파력발전장치로부터 기준 점까지의 거리를 반경으로 한 동심원을 그려 바깥 영역을 설치 유효 영역으로 나타내었다. 이때 동심원의 반경을 정하는 기준점으로 산란파와 방사파의 최대 에너지의 합이 입사파 에너지의 5%와 2%를 만족하는 것으로 하였다. 수치 계산결과를 통하여 얻은 유효 반경과 IEC의 권고안과 비교하였다.

2. 파력발전장치 성능

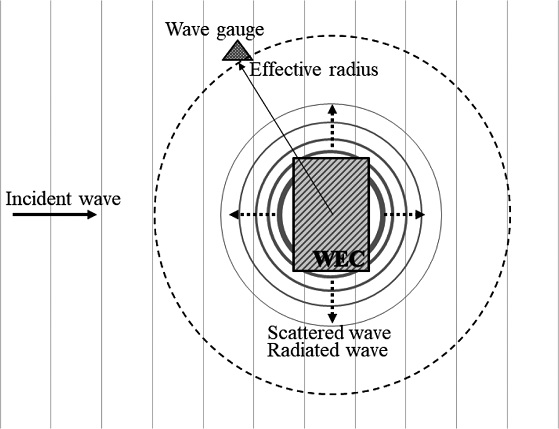
Fig. 1은 파력발전장치 주변 파계(입사파, 산란파, 방사파)를 단순화하여 나타낸 그림이다. 산란파는 입사파의 방향과 파력발전장치의 형상에 따라 바깥 영역으로 전파되는 파의 크기와 형태가 달라진다. 부유체의 운동에 의해 발생하는 방사파의 크기는 부유체의 크기와 형상 그리고 운동 변위에 따라 변한다. 특히, 입사파의 주기와 부유체의 고유 운동주기가 일치될 때 발생하는 공진현상은 방사파의 영향을 크게 증가시킨다. 산란파와 방사파 모두 중심으로부터 멀어질수록 진폭이 감소하면서 퍼져 나간다.

Fig. 1.

Simplified wave field around a wave energy converter.

파력발전장치의 성능을 나타내는 기준값인 입사파의 파워는 산란파와 방사파의 영향이 작게 미치는 위치에서 파고계로부터 측정된 파랑 데이터를 가지고 계산된다. 단위 폭 당 입사파의 파워는 규칙파(밑첨자 reg)와 불규칙파(밑첨자 irr)의 경우 각각 식 (1)과 식 (2)와 같이 계산된다.

여기서, ρ는 해수의 밀도, g는 중력가속도, H는 규칙파의 파고, c_g는 파의 군속도, c는 파의 위상 속도, k는 파수, h는 수심, H_1/3는 유의 파고, T_E는 에너지 주기, m_n은 파랑스펙트럼의 n차 모멘트, k_s (≈1)는 천수 계수(Shoaling coefficient)를 나타낸다.

실해역에서의 파랑에너지는 파고계로부터 측정된 파의 시계열 데이터를 FFT를 이용하여 파랑스펙트럼으로 변환한 후 스펙트럼의 면적과 면적 모멘트를 계산하여 유의파고와 에너지 주기로부터 계산된다.

파력발전장치의 효율은 파력발전장치를 통하여 얻은 전기에너지($$ \overline{P}$$)를 입사파의 단위 폭 당 파랑에너지로 나눈 값으로 다음과 같이 정의된다.

여기서 파력발전장치의 효율(성능)을 정확히 평가하기 위해서는 기준값인 입사파의 파랑에너지를 정확히 알아야 한다.

2.1 입사파 조건

파동장 해석에 사용된 입사파 조건을 Table 1에 나타내었다. 규칙파에서는 파고와 주기를 변화시켜 총 12 case에 대하여 살펴보았고, 불규칙파에서는 유의파고를 2 m로 고정하고, 5개의 피크 주기에 대하여 살펴보았다. Table 1안에 피크 주기 6.65s는 제주도 서쪽 차귀도 해역의 대표 주기로 고정식 구조물의 규칙파와 불규칙 파 조건을 선정함에 있어서 기준값으로 삼았다(Park et al.[2012]). 일방향 JONSWAP 스펙트럼을 이용하여 불규칙파를 생성하였으며, 파동장 시뮬레이션 시간은 규칙파인 경우 60s, 불규칙파인 경우 800s로 잡았다.

Table 1.

Incident wave conditions

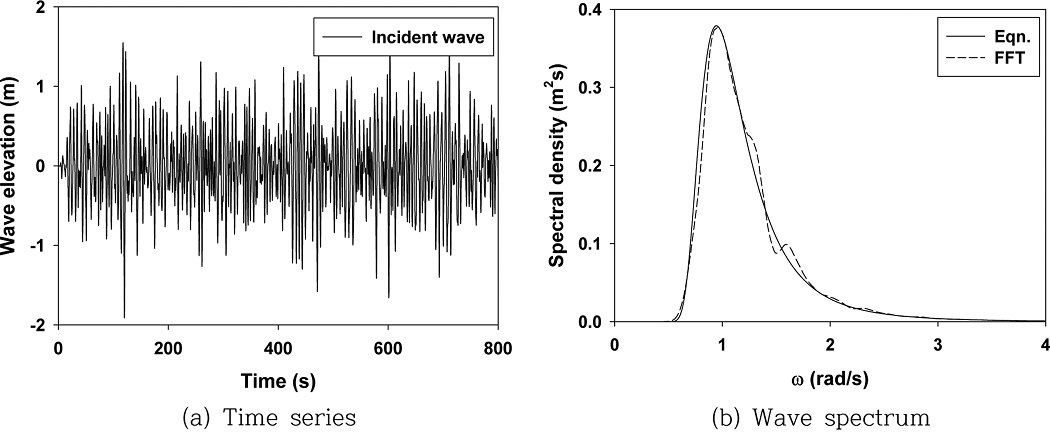
Fig. 2a는 JONSWAP 스펙트럼으로부터 생성된 불규칙 입사파의 시계열 데이터를 보여주고 있으며, Fig. 2b는 생성된 시계열 데이터를 검증하기 위하여 FFT 기법을 사용하여 변환된 파랑스펙트럼과 대상 JONSWAP 스펙트럼(실선)을 함께 비교한 그림이다. 두 스펙트럼이 서로 잘 일치하는 것으로 보아 불규칙파가 적절히 생성되었음을 확인할 수 있다.

Fig. 2.

Time series of generated waves (a) and comparison between the target spectrum and wave spectrum obtain from the time series using FFT technique (b).

2.2 해석 모델

입사파 측정을 위한 파고계의 유효 설치 영역을 선정하기 위한 모델을 고정식과 부유식 파력발전장치로 나누었다. 고정식 파력발전장치의 해석 모델로 제주도 실해역 시험장 1번 정박지에 설치되어 운용중에 있는 진동수주형(Oscillating water column) 용수 파력발전장치를 선택하였다. 진동수주형 파력발전장치는 공기실내의 수면 변동으로 변동압력이 발생하고 외부와의 압력차이로 생긴 공기 흐름이 상부에 설치된 터빈을 회전시켜 전기를 생산하는 발전방식이다. 따라서 공기실내의 변동압력은 방사파를 유도하지만 이를 작다고 가정하여 산란파만 고려하였다. 수심 15 m 해상에 설치된 용수 파력발전장치의 크기는 가로, 세로 각각 31.2 m와 37.0 m이다. Fig. 3a는 실제 용수 파력발전장치의 위성 사진이며, Fig 3b는 파동장 해석을 수행하기 위한 모델을 포함한 계산영역을 보여주고 있다. 수치계산에서 사용한 격자수는 669,000개이며 해석영역의 반경(r)은 50 m이다. 3개의 입사파의 파향에 대하여 살펴보았다.

Fig. 3.

Fixed rectangle-type WEC in Jeju west sea (Yongsu).

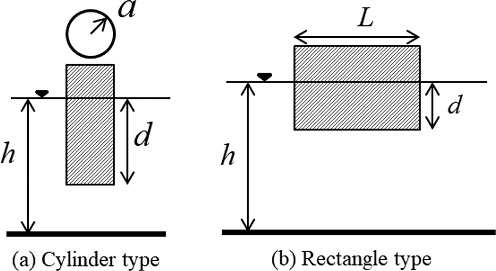
부유식 파력발전장치는 고정식과 달리 부유체의 운동으로 발생하는 방사파가 더해져 더욱 복잡한 파동장을 형성한다. 부유식 파력발전장치의 모델은 원기둥형과 사각형으로 정하고 크기를 변화시켰다. 원기둥형은 흘수를 고정시키고 반경(1m, 3 m, 5 m)을 변화시켰고, 사각형은 가로/세로 길이가 서로 다른 3가지 모델로 정하여 총 6가지 모델에 대하여 살펴보았다. 각 모델의 기본 형상과 제원을 Fig. 4와 Table 2에 나타내었다. 부유식 파력발전장치의 계류 라인의 영향은 무시하였으며 점성에 의한 감쇠력과 PTO 감쇠력은 부유체의 운동에 영향을 주지 않는다고 가정하였다. 축대칭 구조인 원기둥형은 전후(Surge),수직(Heave), 종(Pitch) 방향 3자유도 운동이 일어나지만 사각형은 파향에 따라 6자유도 운동이 모두 발생할 수 있다.

Fig. 4.

Floating cylinder and rectangle-type WEC models.

Table 2.

Specifications of floating WEC models

3. 결과 및 고찰

3.1 고정식 파력발전장치

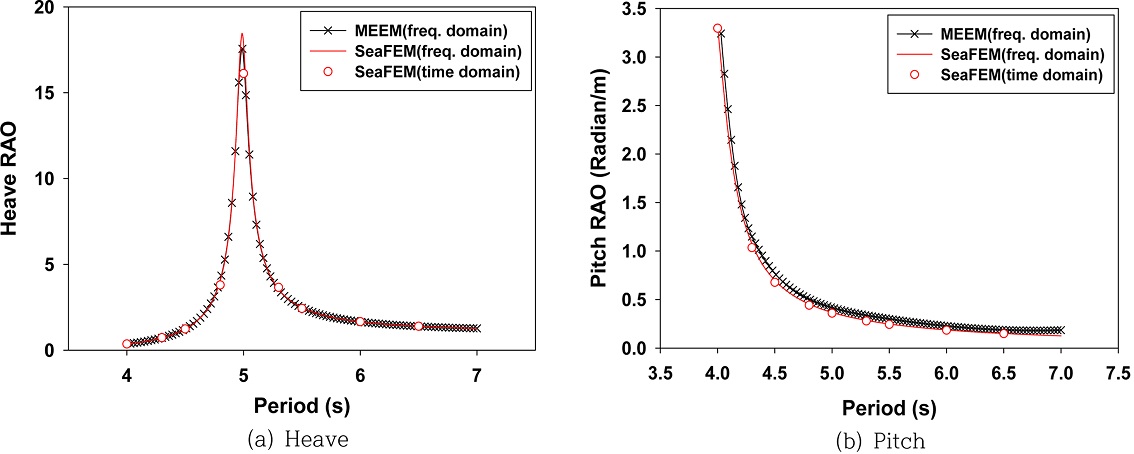
고정식 파력발전장치의 주변 파동장을 수치해석하기 위해 SeaFEM 상용코드를 사용하였다. 먼저 수치해를 검증하기 위하여 고유함수전개법(Matched Eigenfunction Expansion Method:MEEM)을 사용한 해석해와 비교하였다. 포텐셜 이론에 기반을 둔 SeaFEM은 비정렬 격자(Unstructured meshes)에 유한요소법(Finite Elements Method:FEM)을 사용하여 3차원 공간에서 다물체(3D multi-body)의 회절과 방사 문제의 수치해를 제공하는 해석툴로써, 선형 해석 뿐만 아니라 비선형 해석을 포함할 수 있다. 수치해 검증을 위한 해석 모델로 반경 2 m, 흘수 5 m인 원기둥을 채택하였다. 해석결과는 수직, 종 운동 진폭을 입사파의 진폭(A)로 나눈 RAO(Response Amplitude Operator; |z/A|) 값으로 나타냈다. Fig. 5(a)와 (b)는 각각 수직, 종 운동 모드에 대한 RAO로 여기서 검은색 실선( )과 빨간색 실선은 각각 고유함수전개법과 SeaFEM의 주파수 영역 수치계산 결과를 나타내며, 빨간색 동그라미는 시간 영역 계산결과로부터 얻은 RAO 값이다. 모든 결과가 서로 잘 일치하고 있어 SeaFEM의 수치계산 결과를 신뢰할 수 있었다.

Fig. 5.

Comparison of have and pitch RAO of a floating cylinder-type WEC (a = 2 m, d = 5 m).

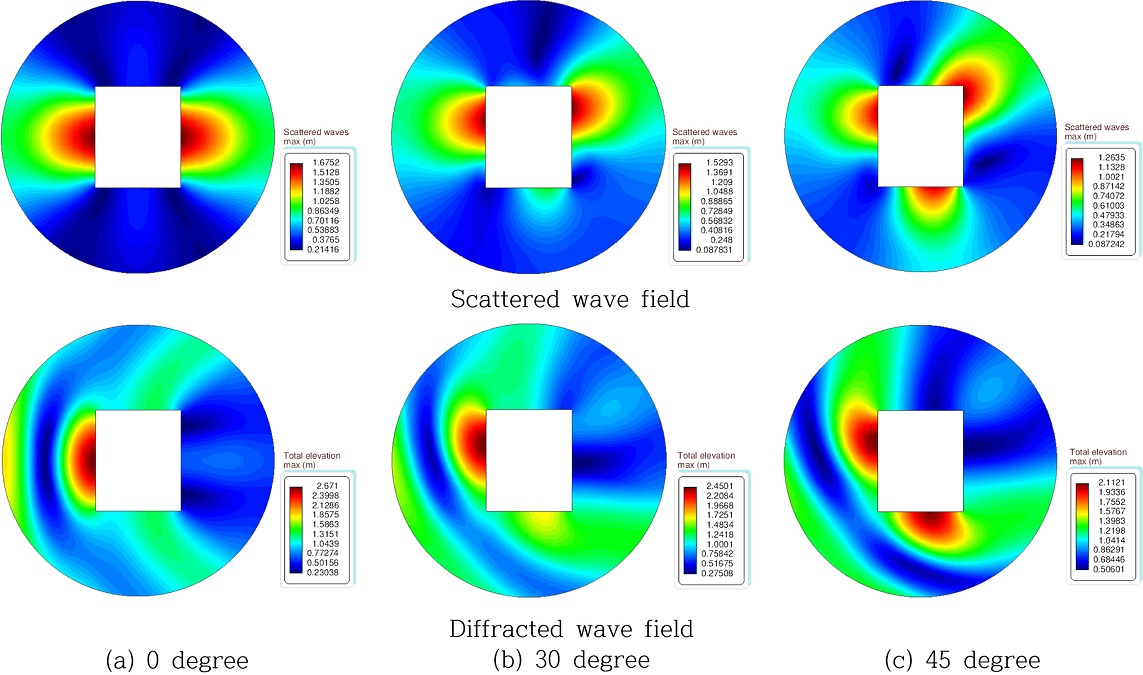
파력발전장치 설치 해역내에서 순수한 입사파 측정을 위한 파고계의 유효 설치영역을 계산하기에 앞서 Fig. 7-9에서 섭동법(Perturbation method)을 사용하여 2차항(Second order)까지 고려한 비선형성을 살펴보았다. 입사파 조건은 파고 2 m, 주기 6.65 s의 규칙파로 Fig. 3(b)에 나타낸 것과 같이 파향이 0, 30, 45도로 고정식 용수 파력발전장치에 입사하였을 때 파력발전장치 주변의 파랑분포를 살펴보았다. 파력발전장치 중심으로부터 x축의 음의 방향으로 25 m, 35 m, 그리고 45 m 떨어진 지점에서의 파랑의 시계열 데이터를 추출하였다(Fig. 3(b)참조). 비선형 효과를 살펴보기 위하여 SeaFEM을 이용하여 선형과 비선형 계산을 각각 수행하였다.

Fig. 6은 선형 해석을 사용하여 파력발전장치 주변의 파랑분포를 3가지 파향에 대하여 산란파의 파동장과 입사파와 산란파가 합쳐진 회절파의 파동장을 그린 그림이다. 파향이 0도 일 때, 산란파의 파동장은 y축에 대칭적으로 나타나지만, 회절파의 파동장을 살펴보면, 입사파와 산란파가 중첩되면서 위상차로 인해 파력발전장치 전면에는 파고가 증가하고 후면에는 파고가 낮아지는 특징을 보이고 있다. 파향이 30도와 45도인 경우에는 입사파가 용수 파력발전장치와 직각으로 부딪히지 않기 때문에 산란파의 영향이 x와 y축에 비대칭적으로 나타난다. 산란파의 진폭은 파력발전장치 주변에서 크게 나타나고 구조물에서 멀어질수록 줄어든다.

Fig. 6.

Scattered and diffracted wave field around a fixed WEC (H=2 m, T=6.65 s).

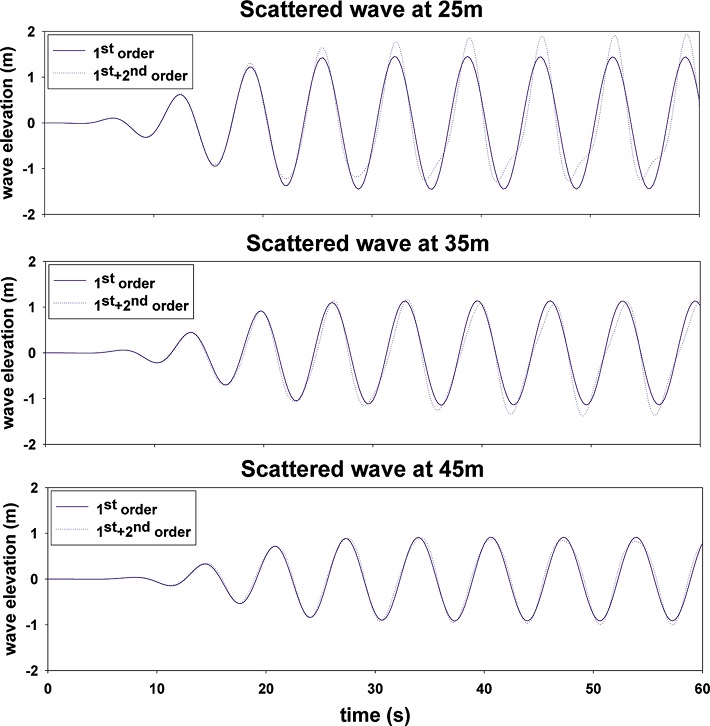
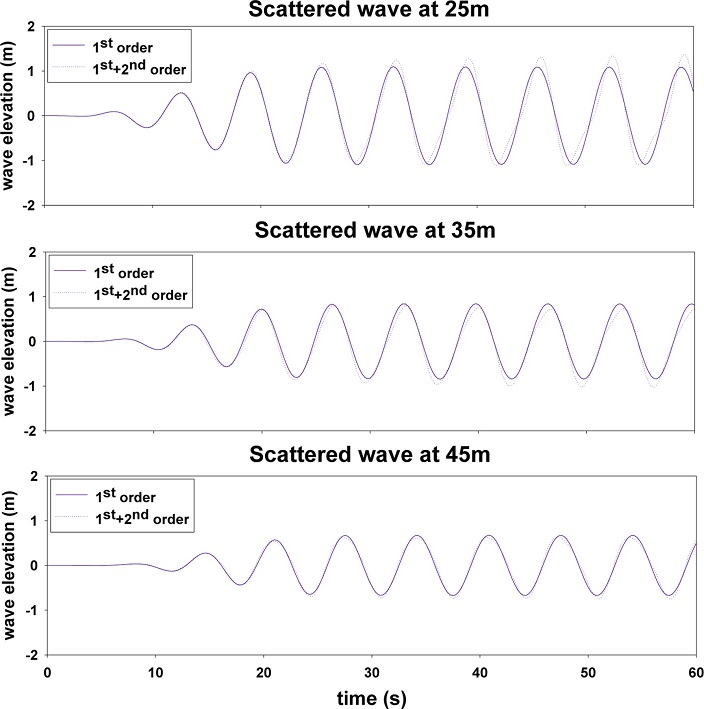
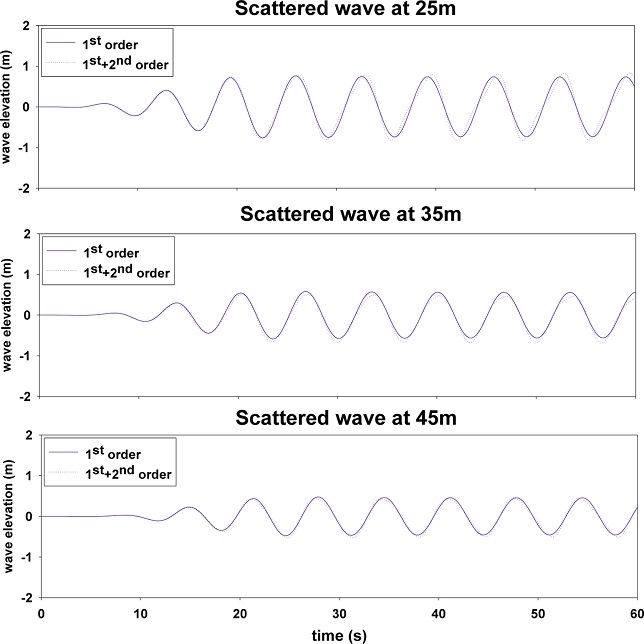
Fig. 7-9는 파력발전장치로부터 떨어진 3지점(25 m, 35 m, 45 m)에서 산란파의 시계열 데이터를 파향(0^o, 30^o, 45^o)에 따라 그린 그림이다. 여기서 실선은 선형 해석 결과이며, 파선은 비선형 해석 결과이다. 파고가 높을수록 파의 비선형성은 증가하기 때문에 산란파의 파고가 상대적으로 높은 파력발전장치와 인접한 25 m 지점에서 비선형성이 크게 나타나 선형 해석결과와 차이를 보인다. 그러나 파력발전장치로부터 점점 멀어질수록 산란파의 파고가 줄어들어 비선형성 효과가 감소하다가 가장 멀리 떨어진 45 m 지점에서는 두 결과가 거의 일치한다. 이러한 경향은 파향이 바뀌어도 동일하게 나타났다. 동일한 파고계의 위치에서 파향별로 비선형성을 비교해 보면 파향이 45도 일 때 비선형성 효과가 가장 작게 나타났다. 이상의 결과로부터 고정식 용수 파력발전장치로부터 어느 정도 떨어진 위치에서는 파의 비선형성은 무시할 수 있으며 선형 해석만으로도 충분히 신뢰할 만한 결과를 얻을 수 있었다. 이후 모든 계산에서는 선형 해석을 수행하였다.

Fig. 7.

Comparison of time series between 1st and 2nd order solutions for zero degree wave angle.

Fig. 8.

Comparison of time series between 1st and 2nd order solutions for 30 degree wave angle.

Fig. 9.

Comparison of time series between 1st and 2nd order solutions for 45 degree wave angle.

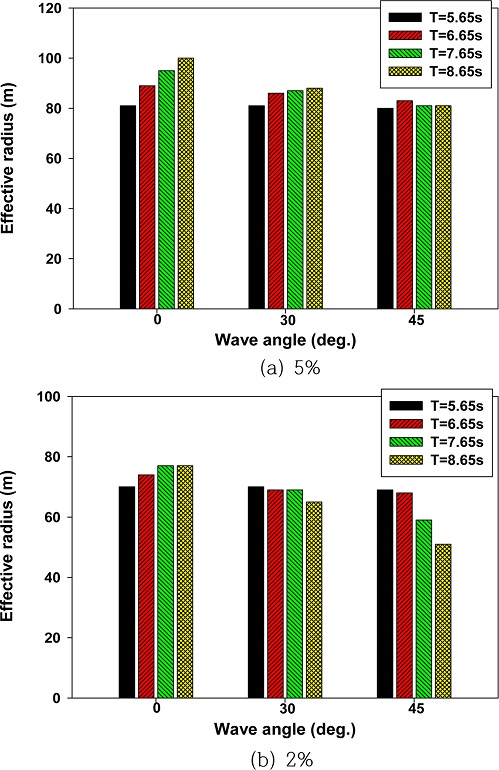
파동장 해석을 통해 고정식 용수 파력발전장치의 중심과 산란파 에너지의 최대값이 입사파 에너지의 5%와 2%에 해당하는 점을 연결한 거리(유효 반경)를 규칙파 조건에서 파향과 주기에 따라 Fig. 10(a)와 (b)에 각각 막대그래프로 나타내었다. 유효 반경은 파향이 0도일 때 가장 크게 나타났다. 특히, 파향 0도에서 파의 주기가 증가할수록 유효 반경이 증가하는 경향을 보였다. 5% 기준일 때 파향 30, 45도에서는 주기에 따른 변화는 적었지만, 2% 기준일 때 파향 45도일 때 주기가 증가할수록 유효 반경은 감소하는 특징을 보였다. 고정식 용수 파력발전장치 주변에서의 산란파의 크기는 입사파의 주기와 파향에 따라 달라지므로 이에 따라 유효 반경이 다르게 나타났다. 각 입사파 조건에 따라 산출된 유효 반경을 Table 3에 정리하였다. 파력발전장치가 설치되는 실제 해역은 계절에 따라 파향이 바뀐다. 따라서 파고계 적정 위치를 정하는 유효 반경은 파향 변화에 따른 최대값을 취하는 것이 안전하다. 한편, Fig. 11은 입사파의 주기와 파고 변화에 따른 유효 반경을 나타낸 막대 그래프이다. 입사파의 주기가 증가함에 따라 유효 반경은 다소 증가하는 경향을 보여준다. 이는 장주기 입사파에서 구조물에 의한 산란파가 증가함을 의미한다. 선형 해석을 이용한 계산결과는 파고 변화에 관계없이 동일한 유효 반경을 주어야 한다. 그림에서 나타난 미세한 차이는 수치계산의 오류로 판단된다.

Fig. 10.

Effective radius of a fixed WEC according to wave periods and incidence angles.

Table 3.

Effective radius for a fixed WEC model according to wave angles and periods in regular waves

Fig. 11.

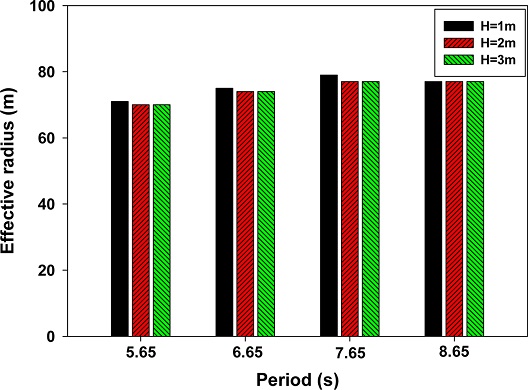
Effective radius for 5% energy ratio of a fixed WEC according to wave heights and periods (wave angle=0 deg.).

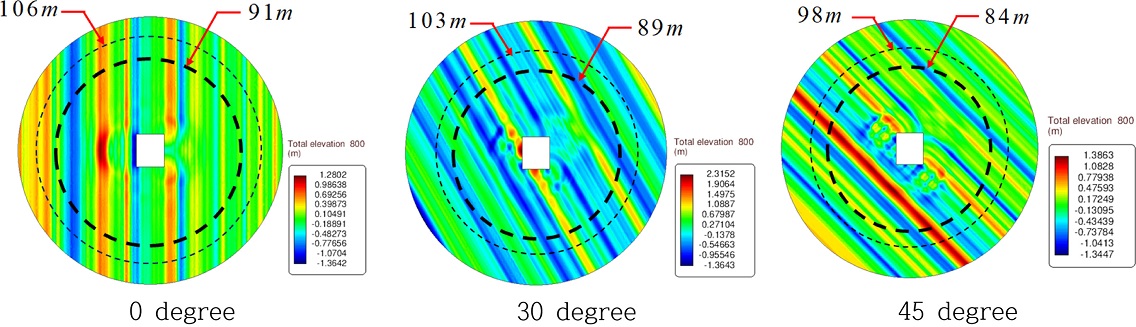
Fig. 12는 불규칙파 조건에서 입사파와 산란파의 합인 회절파의 파동장을 파향별로 나타낸 그림이다. 계산영역의 반경은 150m 이며 총 격자수는 1,435,000개이다. 산란파의 최대 에너지가 5%와 2%에 해당하는 지점을 반경으로 하는 동심원을 함께 그렸다. 5% 기준으로 산출된 유효 반경은 파향 0도, 30도, 45도에서 각각 91 m, 89 m, 84 m이며, 2% 기준으로 낮추었을 때 106 m, 103 m, 98m으로 증가하였다. 규칙파 해석결과와 동일하게 파향 0도에서 가장 큰 유효 반경이 나타났다. 파향별로 산출한 유효 반경을 Table 4에 정리하였다. 이상의 결과로부터 파력발전장치에 입사하는 순수한 입사파를 측정하기 위해서는 중심으로부터 반경 91 m, 106 m을 갖는 동심원 밖에 파고계를 설치하는 것을 권장하며 불가피하게 거리 확보가 어려운 경우, 측정된 파랑데이터 안에는 산란파가 일부 포함되어 있음을 유념해야 한다. 본 연구에서 정한 산란파와 방사파의 합의 최대 에너지가 입사파 에너지의 5%와 2% 기준의 적합성을 나타내기 위하여 IEC TS 62600-100의 규정을 적용하여 유효 반경을 산출하였다. 여기서 IEC 규정은 산란파/방사파 에너지가 최소 90% 이상 감소된 지점으로 IEC 규정을 적용하였을 때의 유효 반경은 68 m이다. 본 연구의 5%와 2% 기준 모두 IEC 기준 을 만족한다. 2% 기준은 필요 이상으로 엄격한 기준으로 판단되며 5% 기준이 파력발전장치 설치 해역내에서 순수한 입사파를 측정하기에 적절한 기준으로 보인다.

Fig. 12.

Diffracted wave field around a fixed WEC in irregular waves (H1/3=2 m, Tp=6.65s).

Table 4.

Effective radius for a fixed WEC model according to wave angles in irregular waves

3.2 부유식 파력발전장치

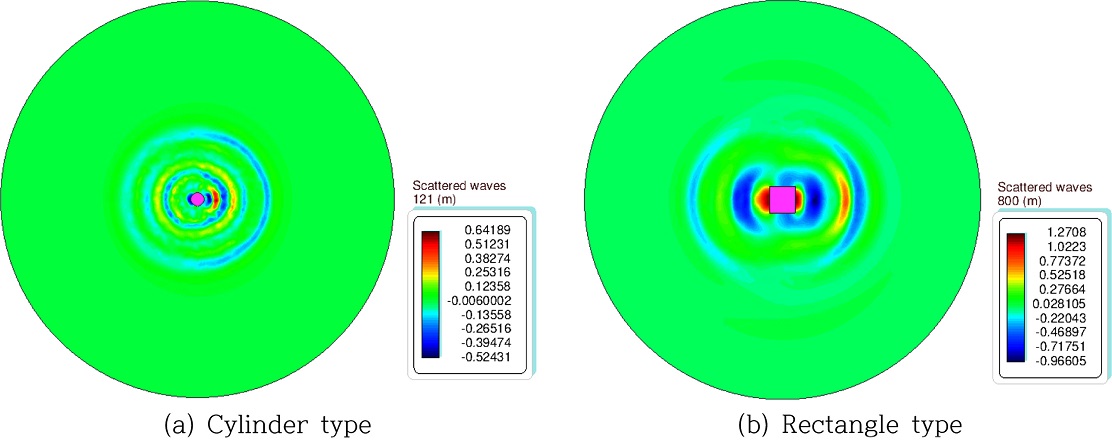
부유식 파력발전장치의 계산 모델은 형상(원기둥형, 사각형)과 크기를 달리하여 총 6개로 잡았고, 불규칙파 조건에서만 해석을 수행하였다. Fig. 13은 원기둥형과 사각형 파력발전장치 주변의 산란파와 방사파를 합친 파동장을 보여주고 있다. 계산에 사용한 총 격자수는 각각 596,000개와 872,000개이다. 고정식과 달리 부유식 파력발전장치에서는 부유체의 운동에 의해 발생하는 방사파가 추가된다. 방사파의 크기는 부유체와 파와의 상대운동이 커짐에 따라 증가한다. 따라서 부유체의 운동이 가장 큰 공진주기에서 방사파의 영향이 가장 크게 나타나며 부유체가 입사파와 함께 움직이는 장주기 영역에서와 부유체의 운동이 적은 단주기 영역에서는 방사파의 영향은 미미하다. 구면파 형태로 퍼져나가는 방사파의 에너지는 산란파와 유사하게 거리에 따라 빠르게 감소된다.

Fig. 13.

Sum of scattered and radiated wave fields for a floating WEC.

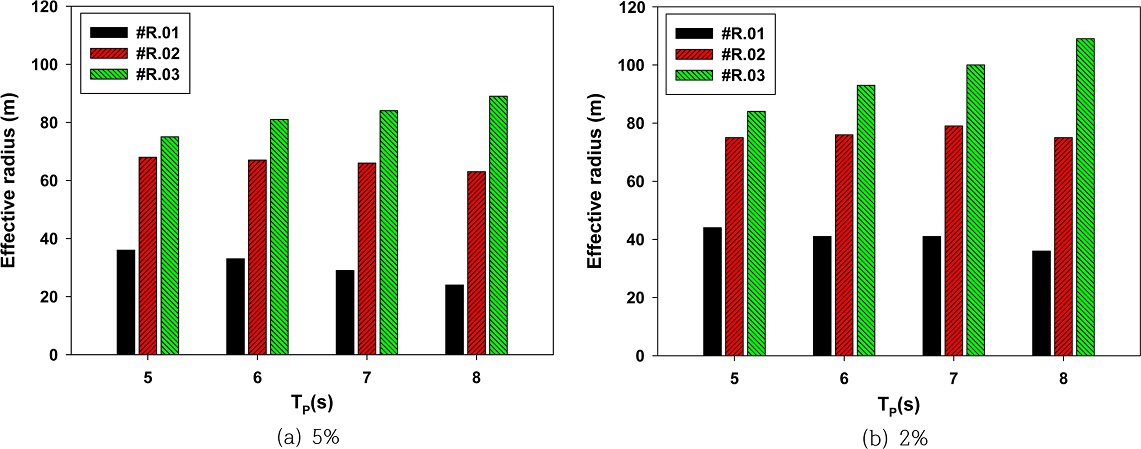
불규칙파 조건으로 파향과 유의파고를 각각 0도와 2m로 고정하고 피크 주기를 5s부터 8s까지 1s 간격으로 변화시켰다. Fig. 14(a)와 (b)는 크기가 서로 다른 3 종류의 사각형 모델에 대하여 입사파 에너지 대비 산란파와 방사파의 최대 에너지의 합이 5%와 2%를 기준으로 산출된 유효 반경을 막대그래프로 나타낸 그림이다. 각 피크 주기에 대하여 모델의 크기가 클수록 방사파와 산란파의 증가로 반경은 증가하는 경향을 보였다. 그러나 각 모델별로는 피크 주기 변화에 따라 다른 경향이 나타났다. 크기가 가장 큰 #R.03 사각형 모델은 피크 주기가 증가하면서 유효 반경이 증가하는 경향을 보였지만, 크기가 가장 작은 #R.01 사각형 모델은 유효 반경이 감소하였다. 이와 같이 모델별로 피크 주기 변화에 따라 유효 반경이 다르게 나타나는 이유는 사각형 모델의 크기가 변함에 따라 각 운동(수직, 종) 모드의 공진주기가 바뀐다. 따라서 운동 변위와 그에 따른 방사파의 크기가 피크 주기에 따라 다르게 나타나기 때문이다.

Fig. 14.

Effective radius for a floating rectangle-type WEC.

반지름이 서로 다른 3 종류의 원기둥형 모델에서 구한 유효 반경을 Table 5에 정리하였다. 원기둥형 모델 중 가장 큰 #C.03 모델은 피크 주기가 가장 짧은 5s에서 유효 반경이 35 m(5%)와 60 m(2%)이며, #C.02 모델은 12 m(5%)와 25 m(2%)로 계산되었다. 계산결과에 따르며, 피크 주기가 증가하면서 산출되는 반경은 점점 감소하였고, 이는 입사파와 부유체간의 상대운동이 장주기에서는 감소되기 때문으로 사료된다. 흘수대비 반경이 가장 짧은 #C.01 모델은 산란파/방사파 에너지가 매우 작아 유효 반경을 추출하기가 어려웠다. 이 경우 파력발전장치와 충돌을 회피할 수 있는 적절한 위치에 파고계를 설치하면 된다. 한편, 현재의 부유식 파력발전장치 모델(#C.03)을 피크 주기 5s에 대하여, IEC TS 62600-100의 규정에 따라 반경을 계산하면 27 m로, 앞에서 살펴본 고정식 모델 결과와 동일하게 현재의 5%와 2% 기준이 IEC 규정을 모두 만족한 것으로 나타났다.

Table 5.

Effective radius for a floating cylinder-type WEC model

4. 결 론

본 연구에서는 실해역 시험장에서 파력발전장치의 성능 평가에 기준이 되는 입사파의 정확한 정보를 얻기 위한 파고계의 설치 위치에 대해 살펴보았다. 이를 위하여 고정식과 부유식 파력발전장치 주변의 파동장 해석을 수행하였다. 포텐셜 코드인 SeaFEM을 이용하여 선형과 비선형 해석 결과를 서로 비교하였다. 파의 비선형성은 파력발전장치 근처에서는 강하게 나타났지만 파력발전장치로부터 멀어지면서 크게 감소하는 것을 확인하였다.

파력발전장치 설치 해역내의 순수한 입사파 측정을 위한 파고계 설치의 유효 영역을 정하기 위한 기준으로 입사파 대비 산란파의 최대 에너지의 비율이 5%와 2%에 해당하는 지점을 선정하고 파력발전장치의 중심과의 거리를 반경으로 한 동심원의 바깥 영역을 파고계 설치의 유효 영역으로 나타내었다. 제주 파력발전 시험장에 위치한 용수 파력발전장치를 고정식 파력발전장치의 해석모델로 잡아 파향, 파고, 주기를 바꿔가면서 규칙파중 파동장 해석을 수행하여 파고계 설치 유효 영역을 나타내었다. 파향이 0도 일 때 유효 반경이 가장 컸고, 여기서 주기가 길어질수록 유효 반경은 증가하였다. 한편, 유의파고 2 m, 피크주기 6.65s인 불규칙파 조건에서의 동심원의 반경은 5%와 2%의 기준에 따라 각각 91 m와 106 m로 나타났고 모두 IEC 규정에 따라 구한 68 m를 만족한다.

부유식 파력발전장치는 원기둥형과 사각형으로 구분하고 크기를 달리하여 총 6가지 해석 모델에 대하여 불규칙파 조건에서의 피크 주기를 바꿔가면서 파고계 설치를 위한 유효 영역을 구하였다. 부유식 파력발전장치에서는 피크 주기 변화에 따른 유효 반경의 변화가 일정한 경향을 보이지 않았다. 이는 부유식 파력발전장치의 경우 산란파의 영향과 함께 방사파의 영향이 나타나기 때문이다. 특히, 방사파는 입사파의 주기와 부유체의 운동 주기와 일치될 때 나타나는 공진시 크게 나타나므로 공진의 유무에 따라 유효 반경의 변화가 생기기 때문이다. 두 종류의 부유식 모델중 원기둥형은 상대적으로 짧은 유효 반경이 나타났다. 크기가 가장 큰 #C.03 모델에서 5% 기준을 만족하는 최대 반경은 35 m이다. 사각형 모델인 경우, 가장 작은 모델인 #R.01은 피크 주기가 길수록 동심원의 반경이 짧게 나타난 반면에, 가장 큰 #R.03은 피크 주기가 길수록 증가하였다. 그리고 피크 주기 8s일 때 5% 기준을 만족하는 반경은 89 m로 가장 컸다.

IEC TS 62600-100의 규정을 적용하여 유효 반경을 계산하여 현재의 계산결과와 비교한 결과, 본 연구에서 제시한 5%와 2% 기준은 IEC 규정과 비교하여 모두 엄격한 기준으로 나타났다. 2% 기준은 다소 과도한 기준으로 평가되며 5% 기준이 적절한 기준으로 판단된다.

Acknowledgments

본 연구는 해양수산부의 해양청정에너지기술개발사업 “파력발전 실해역 시험장 구축”과제의 지원으로 수행되었으며, 연구비 지원에 감사드립니다.

References

• Drew, B., Plummer, A.R. and Sahinkaya, M.N., 2009, A review of wave energy converter technology, Proc. Inst. Mech. Eng. Part A:J. Power and Energy, 223, 887-902. [https://doi.org/10.1243/09576509JPE782]
• IEC-International Electrotechnical Commission., 2012, IEC TS 62600-100.
• Kim, D.E. and Bae, Y.H., 2019, Time domain analysis of optimal arrangement of wave energy converters placed on a floating platform, J. Korean Soc. Mar. Environ. Energy, 22(3), 125-132. [https://doi.org/10.7846/JKOSMEE.2019.22.3.125]
• Kim, J. and Cho, I.H., 2019, Characteristics of Wave Response in a ‘Y’Shape Water Channel Resonator Using Resonance of Internal Fluid. J. Korean Soc. Coast. and Oc. Engr., 31(3), 170-179. [https://doi.org/10.9765/KSCOE.2019.31.3.170]
• Kim, Y.D., Hong, K., Shin, S.H., Kim, K., Lim, C.H., Ko, T.K., Lee, K., Park, J.Y., Kim, J.S., Choen, H.J., Cho, I.H., Bae, Y.H. and Choi, J.S., 2016, Estiablishment Plan of Open SeaTest Bed for Wave Energy Converters, in proc. of KSNRE Spring Meeting, Jeju, 144.
• Lee, C., Kim, M.K. and Cho, Y.J., 2005, Wave Diffraction and Multi-Reflection Around Breakwaters, J. Korean Soc. Coast. and Oc. Engr., 17(4), 232-242.
• Park, J.Y., Shin, S.H., Cheon, H.J., Nam, B.W. and Hong, K.Y., 2012, Experimental study on wave response of pendulum wave energy converter, Proc. of KOSMEE spring meeting, Daegu, Korea, 1465-1470.
• Penney, W.G., Price, A.T., Martin, J.C., Moyce, W.J., Penney, W.G., Price, A.T. and Thornhill, C.K., 1952, Part I. The diffraction theory of sea waves and the shelter afforded by breakwaters, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 244(882), 236-253. [https://doi.org/10.1098/rsta.1952.0003]
• Pos, J.D. and Kilner, F.A., 1987, Breakwater gap wave diffraction: an experimental and numerical study, J. Wtrwy., Port, Coast. and Oc. Engrg., 113(1), 1-21. [https://doi.org/10.1061/(ASCE)0733-950X(1987)113:1(1)]
• Suh, K.D. and Kim, H., 2008, Water wave scattering by partially reflecting breakwaters, KSCE J. Civil Engrg., 12(2), 71-76. [https://doi.org/10.1007/s12205-008-0071-7]
• Wiegel, R.L., 1962, Diffraction of waves by semi-infinite breakwater, J. Hydraulics Division, 88(1), 27-44. [https://doi.org/10.1061/JYCEAJ.0000682]