편심된 회전축을 갖는 수평 원기둥 파력발전장치의 시간영역 해석
초록
파랑중 수평 원기둥의 횡 운동으로부터 최대 파랑에너지를 추출하는 최적의 1차 변환장치(로터)를 설계하기 위하여 선형포텐셜 이론에 기반을 둔 시간영역 해석법을 개발하였다. 시간영역 해석법을 검증하기 위하여 2차원 조파수조에서 모형실험을 실시하였다. 무차원화된 점성감쇠계수가 κ = 0.03일 때 주파수영역 및 시간영역 해석결과는 모형실험결과와 일치하였다. 검증된 시간영역 해석법을 이용하여 3가지 잠긴 깊이(d = 1,6, 2.4, 3.2 m)에 대하여 회전축의 위치를 바꿔가면서 시간평균 추출 파워를 비교하였다. 유의파고 2.0 m, 피크주기 6.65s에 대하여 최대 추출파워는 잠긴 깊이 1.6 m, 회전축의 위치가 lo = 0.75R, α = 300o일 때 일어나며, 이때 시간 평균 추출파워는 약 13.4 kW이다. 이 회전축의 위치에서 수평 원기둥의 횡 운동모드의 고유주기는 입사파의 피크주기와 일치하는 공진조건을 만족한다.
Abstract
In order to extract the maximum wave energy from rolling motion of the horizontal cylinder in waves, the time-domain analysis based on the linear potential theory was developed. To verify the time-domain solution, model test was conducted in a two-dimensional wave tank. The numerical results of both frequency-domain and time-domain agree well with the experimental results when the non-dimensional viscous damping coefficient (κ) is 0.03. As a result of comparing the time-averaged power by changing the positions of the rotating axis and submerged depths with the verified time-domain solution, the maximum time-averaged power (13.4 kW) occurred at the submerged depth 1.6m and position of the rotational axis (lo = 0.75R, α = 300o) for the significant wave height of 2.0 m and peak period of 6.65s. The natural period of the roll motion mode of the horizontal cylinder at this position of rotation axis satisfies the resonance condition coinciding with the peak period of the incident waves.
Keywords:
Wave Energy Converter, Roll Motion, Power Take-Off, Off-centered Rotational Axis, Extracted Power키워드:
파력발전장치, 횡 운동, 파워추출장치, 편심된 회전축, 추출파워1. 서 론
파랑에너지로부터 전기에너지를 추출하는 과정은 먼저 1차 변환장치를 이용하여 파랑에너지를 기계에너지로 바꾼 뒤, 2차 변환장치인 PTO(power take-off)장치를 통하여 전기에너지를 추출한다. 1차 변환장치를 통하여 얻는 기계에너지를 부유체의 운동에너지, 월파의 위치에너지, 공기의 흐름에너지로 구분함에 따라 파력발전장치는 크게 가동물체형, 월파형, 진동수주형으로 나뉜다. 2차 변환장치인 PTO장치로는 부유체의 운동으로 유기된 유체의 압력차로 유압모터를 작동시켜 전기를 생산하는 유압 PTO방식, 유체의 흐름으로 터빈을 돌리는 터빈 방식, 그리고 영구자석과 코일의 상대운동으로 전기를 일으키는 선형 PTO방식이 있다. 유압 PTO방식과 터빈 방식이 기계에너지를 전기에너지로 변환하기에 앞서 유압에너지나 터빈의 회전에너지로 바꾸는 중간 변환단계가 있는 반면에 선형 PTO방식은 직접 전기에너지를 얻는다.
1차 변환장치를 통한 기계에너지를 극대화하기 위해서는 가동물체형인 경우 입사파의 주파수와 부유체의 특정 운동모드의 고유주파수를 일치시켜 운동을 증폭시키는 공진을 활용한다. 또한 진동수주형인 경우도 이와 비슷하게 입사파의 주파수와 닫혀진 공기실내의 고유주파수가 같게 되도록 공기실의 형상을 설계한다. 실제 해상은 다양한 진폭과 주파수가 섞여 있는 불규칙파이나 특정 주파수(피크 주파수, 에너지 주파수)에 에너지가 밀집되어 있으며 특정 주파수의 대역 폭이 좁은 특징(narrow banded spectrum)을 갖는다. 따라서 파랑에너지가 높은 특정 주파수를 입사파의 대푯값으로 잡아 파력발전장치가 공진이 일어나도록 설계한다.
파랑중 부유체의 횡 운동으로부터 파랑에너지를 추출하는 대표적인 1차 변환장치로 Salter[1974]가 제안한 Salter’s duck이 있다. Salter's duck의 단면은 3개의 부분(beak, paunch, stern)으로 구성되어 있어 단면 형상이 복잡하며 정해진 횡 운동 범위를 벗어나면 음의 복원력을 가져 효율이 떨어지는 단점을 지니고 있다. Salter’s duck이 지닌 이런 단점들을 극복하기 위한 시도로 cylindrical duck이나 Bristol cylinder와 같이 형상이 단순한 원형 대칭 단면을 갖지만 편심된 회전축을 두어 Salter’s duck의 비대칭 단면 형상과 동일한 효과를 갖는 연구들이 최근 많은 관심을 받고 있다(Cruz and Salter[2006]; Lucas et al[2009]). 이러한 수평 원기둥 파력발전장치의 성능에 중요한 설계변수로는 원기둥의 반경, 잠긴 깊이, 회전축의 위치, 무게중심의 위치 등이 있다.
본 연구는 수평 원기둥 파력발전장치의 여러 설계변수 중에서 잠긴 깊이와 편심된 회전축의 변화가 파력발전장치의 성능에 미치는 영향을 시간영역 해석법을 통하여 살펴보았다. 수치해석결과를 검증하기 위하여 2차원 조파수조에서 회전축의 위치와 입사파의 주기를 바꿔가면서 수평 원기둥의 횡 운동 변위를 측정하여 수치해석결과와 비교하였다. 시간영역 해석법내의 충격응답함수(impulse response function)와 파력(wave load) 계산에 필요한 횡 방향 유체력(부가질량, 방사감쇠계수, 동유체력, 파기진력)은 선형포텐셜 이론에 기반을 둔 상용코드 WAMIT을 이용하였다. 선형포텐셜 이론에 기반을 둔 현재의 시간영역 해석법은 점성의 효과를 무시하였기 때문에 공진주파수 주변에서 모형실험결과와 정량적인 값 차이를 보인다. 본 연구에서는 두 결과의 정량적인 값이 일치하도록 무차원화된 점성계수를 정하였다. 개발된 시간영역 해석법을 이용하여 설계 파랑조건(유의파고 2 m, 피크주기 6.65s)에서 수평 원기둥의 잠긴 깊이와 회전축의 위치 변화에 따른 횡 운동 변위와 속도 그리고 추출파워의 시계열 값을 구하고 시간 평균값을 산출하였다. 이때 PTO감쇠계수는 주파수영역에서 구한 최적의 PTO감쇠계수의 값들 중에서 최소값을 보이는 공진주파수에서의 값을 사용하였다.
2. 시간영역 해석법
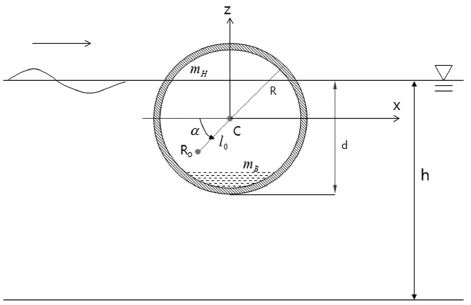
일정한 폭(W)과 반경(R)을 갖는 수평 원기둥 파력발전장치가 입사파의 진행방향과 수직으로 놓여있다. 원기둥의 잠긴 깊이는 d이며, 입사파는 x축의 양의 방향으로 진행한다. 좌표축의 원점은 원기둥의 중심(C)에 위치하며 z축을 연직상향으로 잡았다. 회전축의 중심은 R0이며, 원기둥의 중심(C)과의 상대 위치는 거리(l0)와 각도(α)로 나타낼 수 있다.
수평(sway)과 수직(heave) 운동을 구속한 상태에서 수평 원기둥의 횡(roll) 운동방정식은 Newton의 제 2법칙으로부터 다음과 같이 쓸 수 있다.
| (1) |
여기서 밑첨자 3은 횡 방향을 뜻한다. 따라서 는 횡 운동 가속도이다.
수평 원기둥의 전체 질량(m)을 외형을 이루는 고정 질량(mH)과 흘수를 맞추기 위해 삽입하는 가변 질량(mB)의 합으로 나타내면 전체 관성모멘트(J)도 고정 질량의 기여분(JH)과 가변 질량의 기여분(JB)의 합으로 나타낼 수 있다.
| (2) |
평행축의 정리를 적용하여 회전축(R0) 위치에서의 관성모멘트(JH,JB)는 고정 질량과 가변 질량의 무게 중심 위치인 (0,0)와 (xB,zB)에서의 관성모멘트 값 (IH,IB)을 가지고 아래와 같이 나타낼 수 있다.
| (3) |
여기서 lH=l0과 는 각각 고정 질량과 가변 질량의 무게중심과 회전축 중심간의 거리를 나타낸다.
식 (1)의 오른쪽 항 FT(t)는 파력발전장치에 작용하는 횡 방향의 하중(모멘트)으로 파기진력(Fext(t)), 점성감쇠력(Fvis(t)), 동유체력(Frad(t)), 정유체력(Fres(t)), PTO감쇠력(FPTO(t))의 합으로 표현된다. 본 연구에서는 점성감쇠력을 횡 운동 속도에 선형적으로 비례한다고 가정하였다(). 비례상수인 는 점성감쇠계수이다. 여기서 κ는 무차원화된 점성감쇠계수를, 는 횡 운동모드의 비감쇠 고유주파수(undamped natural frequency)를 나타낸다. 동유체력은 횡 운동 속도에 비례하는 방사감쇠력과 횡 운동 가속도에 비례하는 부가질량력의 합이다.
원기둥 중심(C)에서의 정유체력은 이며, 여기서 는 원기둥 중심에서의 횡 복원력계수이다. 는 각각 원기둥 중심에서의 부력중심과 무게중심의 z 값이다. 회전축 중심에서의 복원력계수(C33)은 Table 1에 나타나듯이 원기둥 중심에서의 복원력계수(C'33)로부터 얻어진다.

Transformation formulas that relate the fluid forces at its geometric center with the fluid forces at an off-centered rotational axis
부유체의 운동에너지로부터 전기에너지를 추출하기 위하여 2차 변환장치인 PTO(power take-off)장치가 필요하다. PTO장치 설치에 따른 PTO감쇠력은 아래와 같이 수평 원기둥의 횡 운동 속도에 선형적으로 비례한다고 가정하였다.
| (4) |
Cho et al.[2018]의 연구결과에 따르면 주파수영역에서 구한 시간 평균 추출 파워가 최대()가 되는 최적의 PTO감쇠계수 는 주파수의 함수로 다음과 같다
| (5) |
여기서 a33(ω),b33(ω)는 횡 방향 운동모드의 부가질량과 방사감쇠계수이다.
실제로 다양한 주파수를 갖는 파들이 섞여 있는 불규칙 파랑 중에서 시시각각 변하는 파랑 변화에 따라 PTO감쇠계수를 식 (5)와 같이 바꿀 수는 없다. 따라서 시간영역 해석법에서는 식 (5)에 나타난 최적의 PTO감쇠계수 중에서 최소값을 보이는 공진주파수에서의 값()을 사용하였다.
식 (1)로부터 시간영역에서의 횡 운동방정식을 다시 쓰면 다음과 같다(Cummins[1962]).
| (6) |
여기서 K33(t)는 이전 시간의 수평 원기둥의 횡 운동의 이력이 현재에 미치는 영향을 나타내는 시간기억함수(time memory function)로 충격응답함수(impulse response function)라 불린다. 충격응답함수 K33(t)는 주파수 함수인 부가질량 또는 방사감쇠계수의 Fourier역 변환으로 구할 수 있다.
| (7) |
식 (6)에 주어진 콘볼루션 적분(convolution integral)을 효율적으로 수행하는 수치해석방법으로 크게 3가지 방법(직접 적분법, Prony법, 주파수영역 식별법)이 제안되었다. Prony 법(Babarit et al.[2005])은 충격응답함수를 복소수 계수(αk)를 갖는 지수함수의 합()으로 나타내어 적분을 수행하는 방법이고, 주파수영역 식별법(frequency-domain identification method, Jefferys[1984]; Damaren[2000])은 충격응답함수를 많은 계산시간이 요구되는 시간영역에서 계산하지 않고 주파수영역에서 계산하는 방식이다. 충격응답함수를 유리함수로 가정하여 분모와 분자에 나타난 다항식의 계수들을 최소자승법(least square method)으로 구한다. 본 연구에서는 직접 적분법(direct numerical integration, Yusong[2008])을 사용하여 콘볼루션 적분을 수행하였다. 식 (6)에서 ω → ∞일 때의 부가질량인 a33(∞)는 주파수영역에서 미리 구해놓은 부가질량을 이용하여 아래와 같이 구할 수 있다.
| (8) |
수평 원기둥이 불규칙파중에 놓여 있을 때 시간영역에서의 파기진력(Fext(t))은 조화함수인 각 파랑성분들을 선형중첩하여 구한다. 파랑스펙트럼(Sζ(ω))과 단위 진폭당 횡 방향 파기진력(X3(ω))이 주어졌을 때 Fext(t)는 다음과 같다.
| (9) |
여기서 ω1=0.1 rad/s, Δω=3.0/Nw rad/s, Nw=300이다. X3(ωn), φ(ωn)는 횡 방향의 파기진력과 위상차를, εn는 범위 [0,2π]내의 난수(random number)를 뜻한다. 식 (9)에서 파랑스펙트럼을 주파수에 대하여 등 간격(Δω)으로 나누지 않은 이유는 일정 시간(2π/Δω) 후에 시간영역 파력이 반복하는 것을 피하기 위함이다. 식 (7),(8),(9)에서 부가질량, 방사감쇠계수, 그리고 파기진력을 얻기 위하여 상용코드 WAMIT을 이용하였다.
계산에 사용한 파랑스펙트럼으로 JONSWAP 스펙트럼을 사용하였다. JONSWAP 스펙트럼은 다음과 같다.
| (10) |
여기서 H1/3은 유의파고, 는 피크주파수이다. ω < ωP 일 때 σ = 0.07이며, ω ≥ ωP 일 때 σ = 0.09이다. 식 (9)에서 파기진력(Fext(t))이 수평 원기둥에 갑자기 힘을 가하는 것을 막기 위하여 램프 함수(ramp function)을 도입하였다. 램프 함수는 S(t) = 3(t/ts)2− 2(t/ts)3이며, 여기서 ts(=5TP)는 램프 함수가 적용된 시간이다.
식 (6)은 적미분 방정식(integro-differential equation)으로 시간에 따라 적분하여 수평 원기둥의 횡 운동 변위, 속도, 가속도의 시계열 값을 구할 수 있다. 다양한 시간 적분 수치해석법(Euler method, 4th order Runge-Kutta method, Predictor-Corrector method)이 많은 학자들(Conte and DeBoor[1980]; Riley et al.[2006])에 의해 제안되었다. 본 연구에서는 Newmark[1959] 방법을 사용하여 시간 적분하였다. 수평 원기둥 파력발전장치의 횡 운동 속도의 시계열 값을 가지고 시간 평균 추출 파워를 구하면 아래와 같다.
| (11) |
여기서 T는 총 발전 시간이다. 본 계산에서는 총 발전 시간을 30분으로 하여 시간 평균 추출파워를 구하였다.
3. 모형 실험
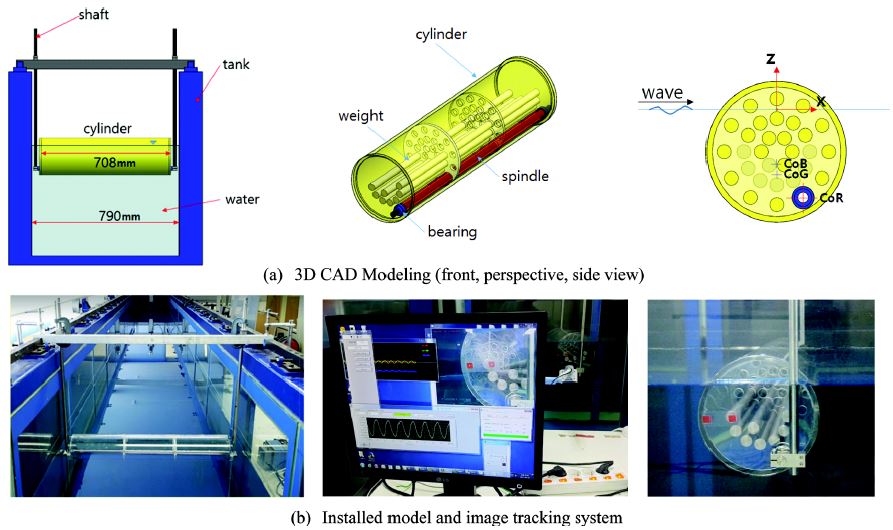
파랑중 편심된 회전축을 갖는 수평 원기둥에 대한 횡 운동 특성을 파악하고 시간영역 해석법을 검증하기 위하여 제주대학교 2차원 조파수조에서 모형실험을 규칙파중에서 실시하였다. 조파수조의 제원은 길이 20 m, 폭 0.8 m, 수심 0.6 m이며, 수조 한 끝 단에 파를 만드는 피스톤 타입의 조파장치가, 다른 끝 단에 투과성 소파장치(공극률 10%, 경사각도 10도)가 놓여있다. 모형실험을 위해 제작한 수평 원기둥의 반경은 0.1 m이며, 잠긴 깊이는 0.16 m이다. 3차원 효과 및 수조 벽면의 영향을 줄이기 위하여 폭(=0.708 m)은 가능한 한 수조 폭에 맞추어 제작하였다. 모형의 재질은 투명한 아크릴이며, 모형의 흘수를 바꿀 수 있도록 원기둥 내부에 여러개의 중량봉을 삽입할 수 있게 제작되었다. 마찰에 의한 기계적 마찰력을 최소화 하기 위해 회전축과 수평 원기둥 사이에 베어링을 삽입하였다. 실험 모형의 자세한 제원은 Table 2에 나타내었다.
모형실험은 PTO장치가 없는 무부하(no-load) 상태에서 실시하였다. 회전축의 위치는 원기둥 중심으로부터 반경의 75%에 위치시켰고, 회전축과 원기둥 중심간의 상대각도(α)는 60°, 120°, 180°로 하였다. 용량식 파고계를 조파기로부터 4m 위치에 설치하여 입사파를 계측하였으며, 수평 원기둥의 횡 운동 변위는 동영상을 이용한 영상추적법(image tracking method)을 이용하여 측정되었다. 이를 위하여 수평 원기둥 단면에 2개의 적색 표시지(marker)를 부착하였다. 입사파의 파고는 0.01 m이며, 입사파의 주기 범위는 1.3s에서 1.9s로 각 실험조건에서 횡 방향 고유주기가 포함되도록 잡았다. Fig. 2(a)는 실험모형을 3차원 CAD로 모델링한 그림이며, (b)는 제작된 실험모형과 영상추적법을 통하여 수평 원기둥의 횡 운동을 실시간으로 모니터링하는 캡처 화면을 보여주고 있다.
4. 계산결과 및 고찰
수치계산에 이용한 수평 원기둥 파력발전장치의 폭(W)과 반경(R)은 각각 5 m와 2 m이다. 잠긴 깊이(d)는 1.6 m, 2.4 m, 3.2m이며, 수심은 80 m이다. 잠긴 깊이(d/R = 0.8, 1.2, 1.6)에 따른 해석모델의 자세한 제원은 Table 3,4,5에 정리하였다. 수평 원기둥에 작용하는 횡 방향 유체력(동유체력, 정유체력, 파기진력)을 상용코드 WAMIT을 이용하여 구하였다. WAMIT 수치계산에 사용한 총 격자수는 1,152개이다. 회전축의 위치가 바뀔 때 마다 유체력을 매번 새로 계산해야 하는 번거로움을 피하기 위하여 Cruz and Salter[2006]가 제안한 축 변환식을 이용하였다(Table 1 참조). Fig. 3은 WAMIT을 사용하여 회전축의 중심에서 직접 얻은 수치계산결과(실선)와 원기둥 중심에서 계산된 수치해를 Cruz and Salter[2006]의 축 변환식을 통하여 동일한 회전축의 중심에서의 값으로 변환한 결과(동그라미)를 비교한 그림이다. 원기둥의 잠긴 깊이는 1.6 m이며, 회전축의 중심은 원기둥 중심으로부터 l0= 0.75R, α = 300o 만큼 떨어져 있다. 두 결과는 서로 완벽히 일치하였다. 이후 모든 계산에서는 축 변환식을 사용하였다.
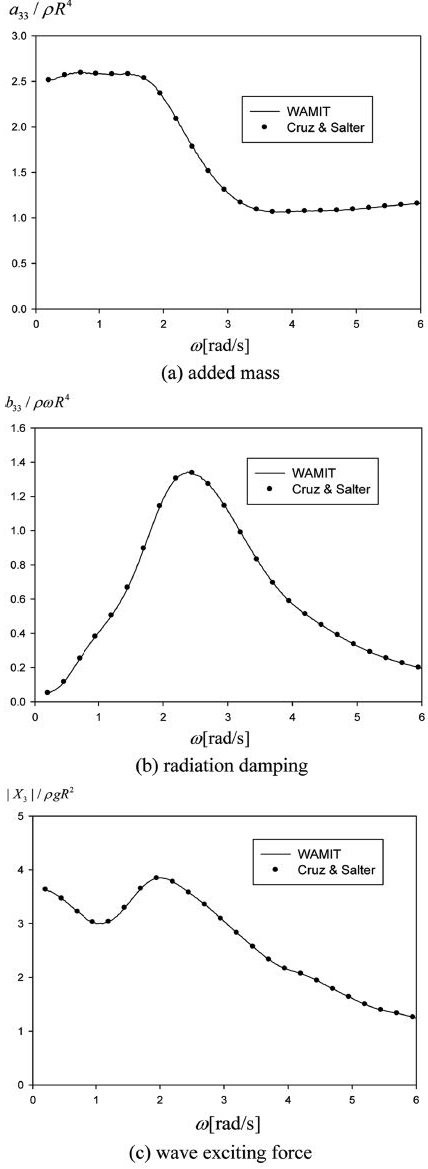
Comparison of the hydrodynamic force and wave exciting force between WAMIT's solutions at off-centered axis (l0 = 0.75R, α = 300o) and numerical results using transformation formula(Cruz and Salter, 2006) for h = 80 m, R = 2m, h = 1.6m, W = 5m.
Fig. 4는 α = 60o, 90o, 120o, 180o 일 때 충격응답함수를 시간에 따라 그렸다. 회전축의 위치에 관계없이 t = 0+에 가까울 때 큰 값을 갖고 급격하게 줄어들다가 일정 시간(t = t*)이 지나면 0에 수렴하는 특징을 보인다. 이러한 충격응답함수 곡선의 특징을 반영하여 식 (6)내의 콘볼루션 적분을 수행할 때 현재의 시간과 관계없이 적분구간의 상한값을 t*로 잡아 효율적으로 수치계산을 수행하였다. 본 연구에서는 t*= 10s로 정하였다. α = 60o, 120o는 회전축이 z축에 대칭되게 놓여 있기 때문에 서로 같은 결과를 준다. α = 90o일 때의 충격응답함수가 α = 60o, 90o, 120o, 180o보다 상대적으로 큰 값을 보이는 것은 이 회전축의 위치에서 수평 원기둥의 횡 운동에 따른 방사감쇠력이 가장 크기 때문이다.
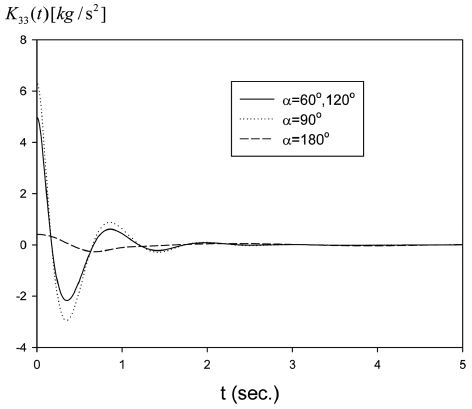
Impulse response function of a horizontal cylinder WEC as a function of α for fixed l0 = 0.75R for R = 0.1 m, d = 0.16 m.
Fig. 5는 모형실험에서 얻은 횡 운동 RAO(Response Amplitude Operator, |ξ3 / A|)를 주파수영역과 시간영역에서 구한 수치해석결과와 비교한 그림이다. 입사파의 진폭은 0.01m이며, PTO장치가 없는 무부하 조건에서의 결과이다. 여기서 큰 기호(●, ○, ▼)는 모형실험의 결과이며, 선은 주파수영역에서 구한 계산결과이다. 작은 기호(●, ○, ▼)는 시간영역 해석법을 통한 계산결과이다. 모형실험 결과와 정량적인 값의 일치를 위하여 수치계산에서는 무차원화된 점성감쇠계수(κ = 0.03)를 동일하게 적용하였다. 수치계산결과와 모형실험결과는 서로 잘 일치하였으며 두 해석법의 결과도 서로 완벽히 일치하였다. 회전축의 위치 변화에 따라 서로 다른 RAO곡선 패턴을 보인다. 흥미롭게도 회전축의 중심이 z축에 대칭으로 놓여있는 α = 60o, 120o의 결과는 비록 같은 공진주기(1.6s)를 갖지만 공진 피크값은 다소 차이를 보이고 있다. 회전축의 중심이 α=180o의 경우 대략 1.0s에서 공진주기가 나타났으며 α = 60o, 120o와 비교하여 작은 횡 운동 변위를 보이고 있다. 이러한 결과로부터 수평 원기둥의 형상과 잠긴 깊이의 변화 없이 단지 회전축의 위치만을 바꿔도 횡 운동의 운동 특성을 쉽게 바꿀 수 있음을 확인하였다. 또한 회전축의 위치에 따라 공진 피크값은 차이를 보인다. 따라서 설치해역의 파랑특성(유의파고, 피크주기)이 주어졌을 때 횡 운동의 공진주기가 에너지 밀도가 높은 피크주기와 일치하도록 수평 원기둥 파력발전장치의 회전축을 위치시키면 공진으로 크게 증폭된 수평 원기둥의 횡 운동 속도로부터 최대 추출파워를 얻을 수 있다.
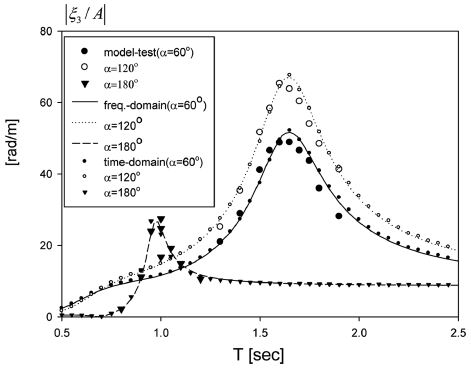
Comparison of roll RAO between numerical(frequency-domain and time-domain) solution and experimental results in regular waves for A = 0.01 m, κ = 0.03, l0 = 0.75R.
Fig. 6은 식 (5)에 주어진 최적의 PTO감쇠계수()를 입사파의 주파수와 원기둥의 잠긴 깊이 그리고 회전축의 위치 변화에 따라 살펴보았다. 주파수의 함수인 최적의 PTO감쇠계수는 저주파수영역에서 큰 값을 갖고 급격히 줄어들다가 어떤 특정 주파수에서 최소값을 찍고 고주파수영역으로 진행함에 따라 다시 증가하는 특징을 보인다. 최소값을 주는 특정 주파수는 식 (6)에 주어진 횡 운동모드의 고유주파수와 일치한다. 실제로 다양한 주파수가 섞여 시시각각 변하는 해상에서 추출파워를 극대화하기 위하여 입사파의 주파수에 따라 PTO감쇠계수를 바꿀 수는 없다. 따라서 시간영역 해석법에서는 파랑의 주파수 변화에 관계없이 일정한 값을 갖도록 고유주파수(ωN)에서의 PTO감쇠계수 를 사용하였다. 공진주파수는 파력발전장치의 잠긴 깊이와 회전축의 위치에 따라 변하므로 도 잠긴 깊이와 회전축의 위치에 따라 변한다.
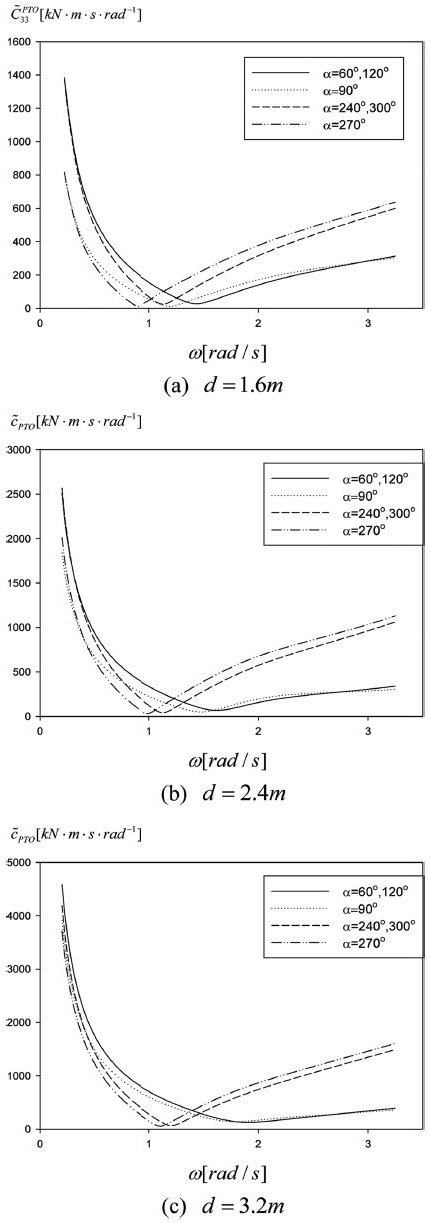
Optimal PTO damping coefficient as a function of wave frequency ω and α for fixed l0 = 0.75R, κ = 0.03.
Fig. 7은 진폭(A) 0.5 m, 주기(TW) 6.65s인 규칙파에 대하여 수평 원기둥의 잠긴 깊이가 바뀔 때 횡 운동 변위와 속도의 시계열 곡선을 보여주고 있다. 회전축 중심의 위치는 l0= 0.75R, α = 120o이다. 잠긴 깊이 d = 1.6m, 2.4m, 3.2m에 대한 횡 운동의 고유주기(TN)는 각각 4.43s, 3.77s, 3.21s이다. 또한 고유주파수(ωN)에서의 PTO감쇠계수 는 26.9 kNm/(rad/s), 67.2 kNm/(rad/s), 127.1 kNm/(rad/s)이다. 특정 회전축(l0= 0.75R, α = 120o)에서 3개의 잠긴 깊이는 모두 공진조건에서 크게 벗어나 있다. 횡 운동 변위와 속도를 비교한 결과 잠긴 깊이가 가장 낮은 d = 1.6m에서 횡 운동 변위와 속도가 가장 크게 나타났다. 잠긴 깊이 d = 2.4m가 d = 3.2m보다 횡 운동 변위와 속도가 증가하였다. 즉, 공진 조건을 만족하지 않았을 때 잠긴 깊이가 낮을수록 횡 운동 변위와 속도는 커짐을 알 수 있다.
WEC's rolling response(a) and velocity(b) for two different WEC’s submerged depths for A = 0.5m, TW = 6.65 s, κ = 0.03, l0 = 0.75R, α = 120o.
Fig. 8은 시간영역 해석법을 불규칙파로 확장하였을 때 최적의 회전축의 위치를 찾는 그림이다. 본 계산에서 사용한 불규칙파는 γ = 2.2인 JONSWAP 스펙트럼이다. 유의파고와 피크주기는 각각 H1/3= 2.0 m, TP= 6.65s이다. 회전축의 중심과 원기둥 중심간의 거리를 l0= 0.75R로 고정시키고 상대 각도(α)를 0부터 360도까지 10도씩 증가시키면서 식 (11)에 주어진 시간 평균 파워를 극 좌표계로 나타내었다. 단위는 [kW]이다. 3가지 잠긴 깊이에 대하여 살펴보았다. 먼저 잠긴 깊이가 상대적으로 깊은 d = 3.2m인 경우, 불규칙파중 시간평균 파워의 최대값은 대략 α = 100o에 위치한다. 전반적으로 회전축이 수면 아래 놓일 때가 수면 위에 위치할 때 보다 시간평균 추출파워가 상대적으로 크게 나타났다. 그러나 잠긴 깊이가 d = 1.6m, d = 2.4m인 경우, 회전축의 중심이 수면 위에 놓일 때가 수면 아래에 놓일 때 보다 큰 파워 값을 준다. 시간평균 추출파워의 최대값을 주는 회전축의 위치는 α = 300o 근방이다. α = 300o 주변에서 최대 추출파워를 주는 이유는 이 위치에서 횡 운동모드의 고유주파수가 입사파의 피크주파수와 일치하는 공진조건을 만족하기 때문이다. 3가지 잠긴 깊이에 대하여 회전축의 위치를 바꿔가면서 시간평균 추출파워를 비교한 결과, 최대 추출파워는 잠긴 깊이 1.6 m, 회전축의 위치 α = 300o에서 일어나며 이때 시간 평균 추출파워는 약 13.4 kW이다.
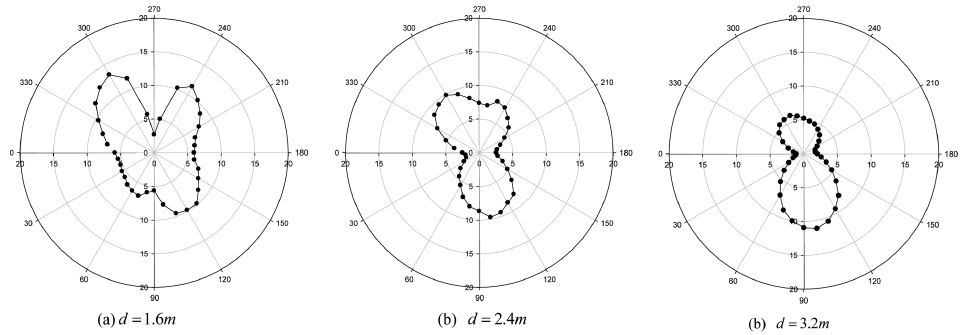
Comparison of polar plot of time-averaged extracted power [kW] as a function of α for H1/3 = 2.0 m, TP = 6.65s, γ = 2.2, l0 = 0.75R, κ = 0.03.
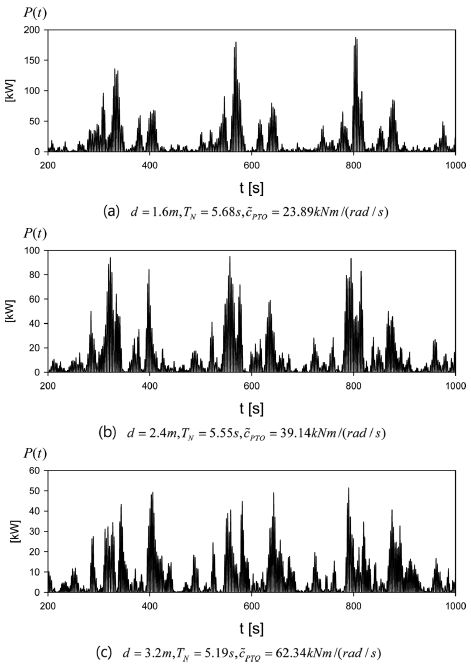
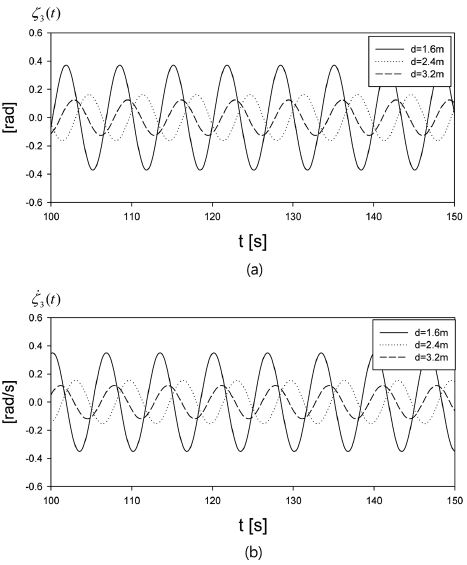
Fig. 9와 10은 3가지 잠긴 깊이(d = 1.6 m, 2.4 m, 3.2 m)에 대하여 시간에 따른 횡 운동 변위와 추출파워를 보여주는 그림이다. Fig. 8를 참조하여 잠긴 깊이 d = 1.6m, 2.4m에서 시간평균 추출파워가 최대가 되는 회전축의 위치(l0= 0.75R, α = 300o)를 잡았다. 회전축의 위치 l0= 0.75R, α = 300o에서 각 잠긴 깊이에서의 횡 운동모드의 고유주기는 각각5.68s, 5.55s, 5.19s이다. 각 잠긴 깊이에 대응하는 고유주기에서의 최적의 PTO감쇠계수는 각각 23.89 kNm/(rad/s), 39.14 kNm/(rad/s), 62.34 kNm/(rad/s)이다. 횡 운동 변위와 추출파워 모두 불규칙한 입사파에 따라 불규칙한 거동을 보여주고 있다. 총 30분간 얻은 추출파워의 시계열 자료를 시간 평균한 값은 잠긴 깊이 1.6 m, 2.4 m, 3.2 m에 대응하여 각각 13.4 kW, 9.9 kW, 5.8 kW이다. 잠긴 깊이가 상대적으로 작을 때의 횡 운동 변위와 추출파워가 커졌다.
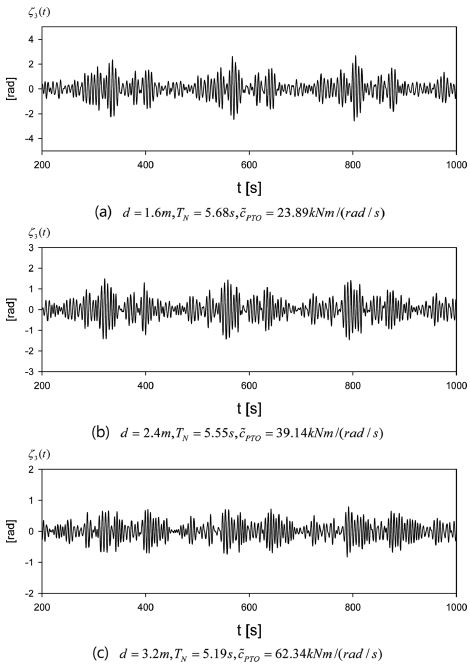
Time series of roll motion at three different drafts in irregular waves for H1/3 = 2.0 m, TP = 6.65s, κ = 0.03, l0 = 0.75R, α = 300o.
4. 결 론
수평 원기둥의 잠긴 깊이와 회전축의 위치는 횡 운동모드의 고유주파수의 정량적인 값을 결정하는데 중요한 변수이다. 대부분 가동물체형 파력발전장치는 최대 추출파워를 얻기 위해서는 입사파의 주파수와 특정 운동모드의 고유주파수를 일치시켜 공진을 발생시킨다. 따라서 설치해역의 파랑조건이 주어졌을 때 수평 원기둥 파력발전장치의 잠긴 깊이와 회전축의 위치를 적절히 잡으면 공진으로 크게 증폭된 수평 원기둥의 횡 운동 속도로부터 최대 추출파워를 얻을 수 있다.
PTO장치가 없는 무부하 상태에서 주파수영역과 시간영역에서 구한 수치해석결과는 모형실험결과와 잘 일치하였다. 또한 주파수영역과 시간영역 해석법의 수치해석결과의 동일함을 확인함으로써 시간영역 해석법을 검증하였다. z축에 대칭으로 놓여있는 α = 60o, 120o의 결과는 동일한 공진주기(1.6s)를 갖지만 공진점에서의 피크값은 α = 120o에서 더 크게 나타났다. 회전축의 중심이 α = 180o의 경우 공진주기가 1.0s에서 나타났으며 α = 60o, 120o와 비교하여 공진 피크값의 크기는 상대적으로 작았다. 즉, 회전축의 위치 변화에 따라 수평 원기둥의 공진주기는 달라지며 공진점에서의 횡 운동변위의 정량적인 값에서도 차이를 보인다.
설치 해역의 파랑조건(H1/3= 2.0m, TP= 6.65s)에 대하여 시간영역 해석을 수행하여 횡 운동 변위, 속도, 추출파워를 시간에 따라 살펴보았다. 불규칙 파랑중 수평 원기둥 파력발전장치의 최적 형상을 찾기 위하여 3가지 잠긴 깊이(d = 1.6m, 2.4 m, 3.2 m)에 대하여 회전축의 위치 변화에 따른 추출파워의 시간평균 값을 살펴보았다. 잠긴 깊이가 상대적으로 깊으면 회전축을 수면 아래에 위치시키고 반대의 경우 수면 위에 위치시키는 것이 추출파워를 증가시키기에 유리하다. 공진조건의 만족 여부를 떠나 잠긴 깊이가 낮으면 상대적으로 횡 운동 변위와 속도 그리고 추출파워가 커지는 것을 확인하였다. 3가지 잠긴 깊이에 대하여 회전축의 위치를 바꿔가면서 시간 평균 추출파워를 비교한 결과, 최대 시간평균 추출파워(13.4 kW)는 잠긴 깊이 1.6 m, 회전축의 각도 α = 300o에서 일어나며 이때 수평 원기둥의 횡 운동모드의 고유주기는 입사파의 주기와 일치하는 공진조건을 만족한다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20163010071690).
References
- Babarit, A., Duclos, G., Clement, A.H., (2005), Comparison of Latching Control Strategies for a Heave Wave Energy Device in Random Sea, Appl. Ocean Res, 26, p227-238.
-
Cho, I.H., Koh, C.H., Bae, Y.H., (2018), Performance Analysis of a Horizontal Cylinder Wave Energy Converter with Off-centered Rotational Axis, J. Korean Soc. Mar. Environ. Energy, 21(1), p1-13.
[https://doi.org/10.7846/jkosmee.2018.21.1.10]

- Conte, S.D., DeBoor, C., (1980), Elementary Numerical Analysis: An Algorithmic Approach, McGraw-Hill Ed., New York.
- Cummins, W., (1962), The Impulse Response Function and Ship Motions, Schiffstechnik, 9, p101-109.
-
Cruz, J., and Salter, S.H., (2006), Numerical and experimental modelling of a modified version of the edinburgh duck wave energy device, Proc. IMechE PartM- J. of Eng. for the Maritime Environ, 220, p129-147.
[https://doi.org/10.1243/14750902jeme53]

- Damaren, C.J., (2000), Time-domain Floating Body Dynamics by Rational Approximation of a Radiation Impedance and Diffraction Mapping, Ocean Eng, 27, p687-705.
-
Jefferys, E.R., (1984), Simulation of Wave Power Devices, Appl. Ocean Res, 6, p31-39.
[https://doi.org/10.1016/0141-1187(84)90026-9]

- Lucas, J., Salter, S.H., Cruz, J., Taylor, J., Bryden, I., (2009), Performance optimization of a modified duck through optimal mass distribution, Proc. of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden.
- Newmark, N.M., (1959), A method of computation for structural dynamics, Proc. of the American Society of Civil Engineers, p67-94.
- Riley, K.F., Hobson, M.P., Bence, S.J., (2006), Mathematical Methods for Physics and Engineering, Cambridge University Press, Cambridge.
- Salter, S.H., (1974), Wave power, Nature, 249, p720-724.
-
Yusong, C., (2008), A procedure for evaluation, assessment and improvement of added mass and radiation damping of floating structures, 27th International Conference on Offshore Mechanics and Arctic Engineering, 2008-57275.
[https://doi.org/10.1115/omae2008-57275]