HNS 확산 예측정확도 향상을 위한 황해 연안 조화상수 데이터베이스 격자해상도 개선

2.1 광역 모델 한계 분석

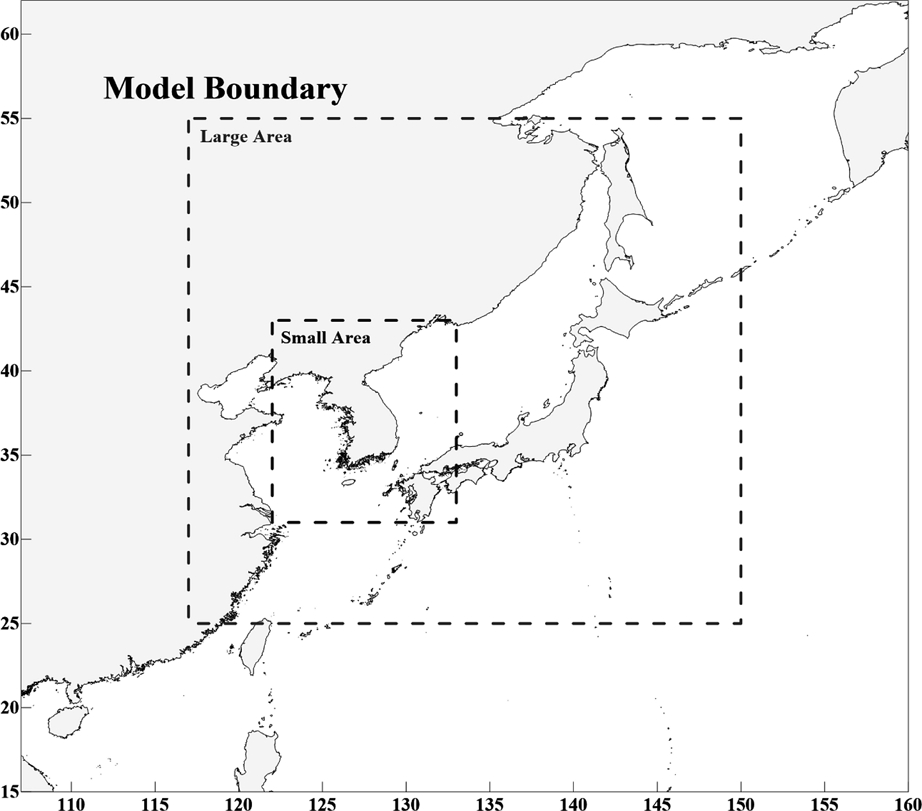
동북아 인근 조화상수 Database 구축 목적으로 2018년을 기준으로 우리나라를 중심으로 한 동북아(25°N~55°N, 117°E~150°E) 3분(약 5.4 km) 간격, 한반도 인근(31°N~43°N, 122°E~133°E) 1분(약 1.8 km) 간격으로 Fig. 1과 같이 조류 예측을 수행하였다.

Fig. 1.

Wide-area tidal current prediction model boundary in Northeast Asia.

수치모델 경계 설정을 위해 Nao.99Jb(National Astronomical Observatory of Japan) 일본 인근 해역 조류 조화상수 모델 데이터를 사용하였다. Nao.99b 및 Nao.99Jb 모델은 TOPEX/POSEIDON의 고도계 데이터를 이용하여 전 지구 및 일본 지역 조류를 약 5년간 수치모델링 하여 만든 조화상수 데이터베이스로 격자별(1/2도, 5분)로 데이터를 읽을 수 있으며, 16가지 분조(M2, S2, K1, O1, N2, P1, K2, Q1, M1, J1, OO1, 2N2, Mu2, Nu2, L2, T2)에 대해서 사용할 수 있다(Matsumoto et al.[2000]). 조류 예측을 위해 MOHID 모델을 400일간 수행하였다. MOHID 모델은 삼차원 비압축성유체에 대한 방정식을 계산하며, 정수압은 Boussinesq와 Reynolds 근사를 가정하고, 직교 좌표계에서 모델의 x, y, z 방향의 운동방정식, 연속방정식, 정수압 방정식은 각각 다음 식과 같이 정의한다.

여기서, u, v, w는 각각 x, y, z 방향으로의 속도 벡터 성분, f는 코리올리 파라미터, ν_H, ν_t는 수평/수직 방향에서의 난류 점성(turbulence viscosity), ν는 분자 동점성 계수(molecular kinematic viscosity), p는 압력, g는 중력가속도, ρ는 밀도이다. 난류 모델은 k−ε 모델을 사용하였으며, 운동량 및 물질이동 항은 1-2-3차 오더의 전방차분법, 중앙차분법, TVD(Total Variation Diminishing) 방법을 적용하였다. 조류 단일 조건에서 모델을 구성하고 다른 변수에 의한 변화를 통제하기 위해 수온, 염분값은 상온 및 30 psu에서 변하지 않도록 고정했으며, ρ값은 수온과 염분에 의해 초기 지정한 값에 의해 고정된다. 연직경계조건의 경우 표층에서의 플럭스 및 응력은 0으로 가정하였고, 저층에서는 해저면과 수층의 전단응력은 다음 식과 같이 결정하여 사용하였다.

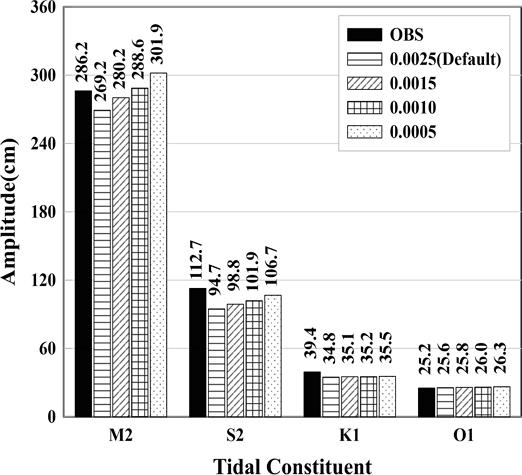
여기서, C_D은 유체-저면의 항력 계수, k는 von Karman 상수, $$ z_0^b$$는 Bottom roughness length이다. $$ z_0^b$$의 경우 저층에 인접한 격자에서 발생하는 유속과 전체 격자의 수심에 따라서 결정된다. $$ z_0^b$$는 Bottom absolute rugosity(이하 rugosity)로 제어되며, rugosity의 초기 설정값(Default)은 0.0025 m이다. 경계조건 설정 이후 초기 설정값으로(Default) 검증실험 시 경기만 인근에서 M2, S2 분조의 진폭이 관측값에 비해 낮게 모의되고, 태안 기준 북측 해상으로 올라갈수록 S2 분조의 진폭/위상 오차가 증가하는 경향이 나타나 마찰계수를 조정할 필요가 있었다. rugosity값의 모형 반응을 알아보기 위해 인천항에서 0.0025 m, 0.0015 m. 0.0010 m, 0.0005 m 4개 조건으로 비교실험을 진행하였는데, 동북아 해역을 기준으로 rugosity값이 감소할수록 진폭이 증가하는 효과를 보였으며, 마찰계수가 0.0010 m 일 경우 최적의 결과를 나타냈다(Fig. 2).

Fig. 2.

Comparison of tide amplitude change in Incheon Port through friction coefficient adjustment.

수치모델은 기간을 1년 이상 수행하고 조화분해를 실시하였다. 조위 검증은 국립해양조사원 기본수준점 4대분조(M2, S2, K1, O1) 자료를 이용하였으며, 인천항(T1), 군산항(T2), 여수항(T3), 부산신항(T4), 포항항(T5), 동해항(T6), 제주항(T7), 서귀포항(T8), 가거도(T9), 독도(T10) 총 10곳에서 진행하였다. 조류 검증은 국립해양조사원 과거 관측자료 중 백령도-대청도 인근 해상(C1; 12BY01), 연평도 남동쪽 30 km 해상(C2; 07GG12), 어청도 남서쪽 30 km 해상(C3; 00KS-3), 맹골도 인근 해상(C4; 06YME7), 여수 인근 해상(C5; 06YS10) 총 5곳에서 진행하였다. 조위의 경우 Table 1과 같이 분조별 오차는 동해를 제외한 지점에서 최대 약 10% 내외로 나타났으며, 동해항, 포항항, 독도의 경우 관측값의 진폭이 작아 비교적 오차율이 크게 나타났으나, 정점별로 1.4 cm, 1.4 cm, 0.5 cm 이내의 오차를 보여 큰 차이가 없는 것으로 판단하였다. 조류의 경우 동방성분과 북방성분으로 u, v 방향을 분리하여 분석하였으며, Table 2와 같이 결과를 산출하였다. 조류의 경우 C5를 제외한 4곳에서 진폭 합에 대한 오차는 20% 이내이나, C5의 북방성분의 오차는 51.5%로 크게 나타났다. 격자 크기 및 모양에 따른 수치모델 결과를 비교한 연구사례를 보면 격자가 조밀하지 않을수록 저면 마찰과 Numerical viscosity의 증가를 초래하였으며, 유속 및 수위를 변화시키는 중요한 변수로 작용하였다(Bomers et al.[2019]). 관측 위치 인근의 지형과 섬을 실험 격자로 재현하지 못하여 오차가 크게 발생한 것으로 판단된다.

Table 1.

Amplitudes and phase of Major tidal components and Observation-Model (Northeast Asia Area) for T1-T10 Stations

Table 2.

Amplitudes and phase of Major tidal current components and Observation-Model (Northeast Asia Area) for C1-C5 Stations

2.2 황해 연안 상세역 구축

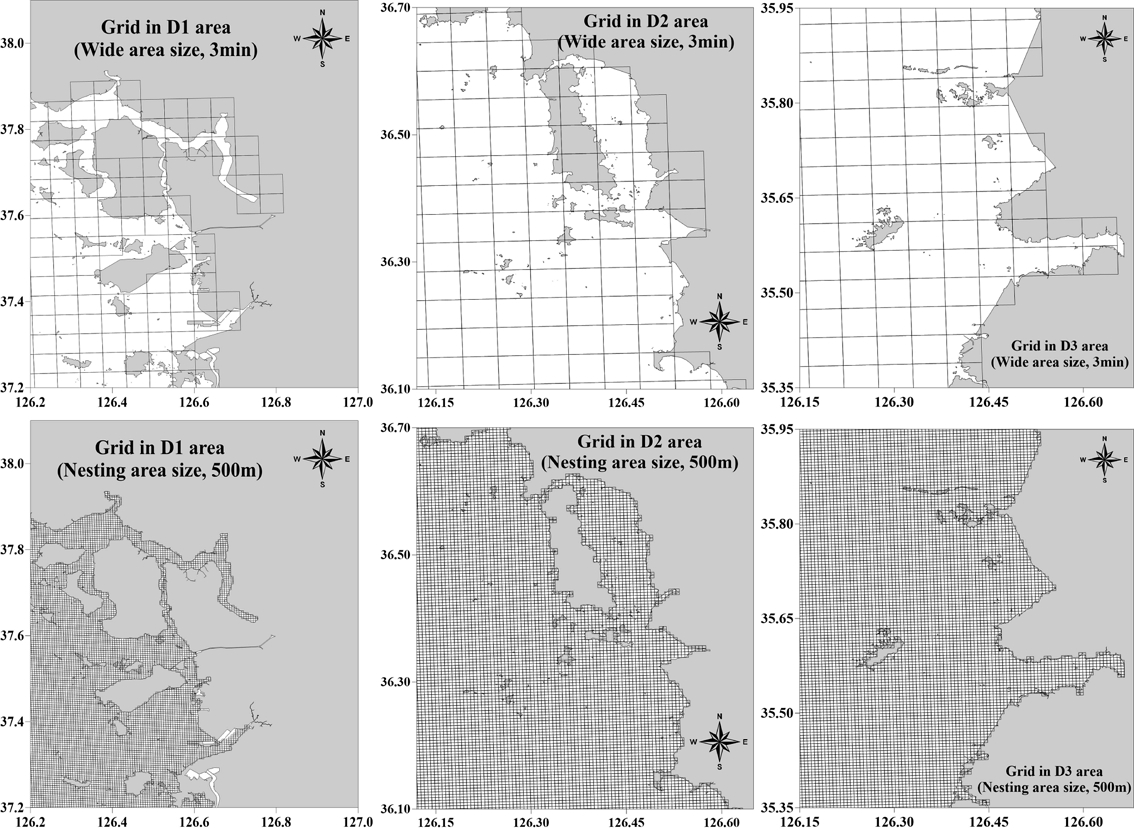
동북아 광역 모델에서 외해에서의 조류 예측정확도는 높게 나타났으나, 연안 인근의 조류관측점에서의 정확도는 크게 저하되었다. 조위의 경우 연안 인근 격자해상도가 높지 않아도 Fig. 2 인천항 사례와 같이 예측정확도가 높을 수 있으나, 황해의 많은 조간대 지역과 섬들로 인해 조류에 대한 3분, 1분 격자에서의 정확한 예측은 사실상 불가능하다. 이에 따라 연안 인근에서의 격자해상도를 증가하기 위해 경기만, 태안, 새만금 인근 해역에 대한 0.5 km 간격의 정밀한 조류 예측이 필요하다고 판단하였다. 연안 인근에서의 예측을 위해 광역 모델과 연계하여 내삽(Nesting)을 실시하였으며, 격자 크기는 0.5 km 간격으로 구성하였다. 원활한 실험을 위해 경기만, 태안, 새만금 해역을 분리하였으며, 각각 D1, D2, D3 영역으로 정하였다. 동북아 영역 모델에서 해안선이 부정확했던 경기만 연안 지역과 평택항 인근의 경우 격자해상도가 증가함에 따라 조간대 지역과 한강 하구, 인천 신항, 평택항 등을 정확하게 재현할 수 있었다(Fig. 3). D2 영역은 태안부터 비응항까지 포함하였으며, D3 영역은 비응항부터 낙월도까지 설정하여 연안 인근 조간대 및 하구역에 대해 재현토록 하였다. 모델 수심은 광역과 상세역 모두 2021년에 발간된 수치해도를 기준으로 적용하였다.

Fig. 3.

Comparison of shoreline resolutions between wide-area grids and nesting grids (D1, D2, D3).

2.3 상관관계 및 오차 분석

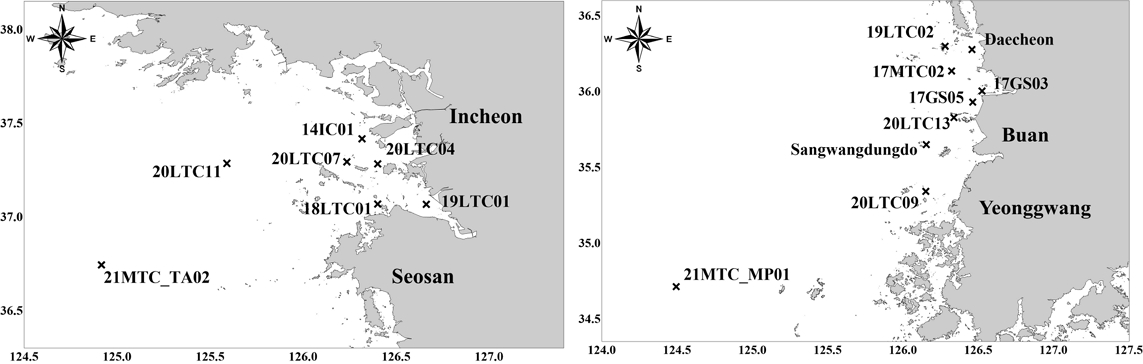
조류 예측 결과의 정확도 향상 정도를 파악하기 위해 모델 결과를 검증하였다. 국립해양조사원의 과거 관측자료와 해양관측부이 유속 관측자료 중 지역별 우세 분조 및 천해분조를 포함하기 위해 국립해양조사원에서 제공하는 30주야 이상의 관측자료를 사용하였다. 조화분해는 Nao.99Jb 16개 분조를 기준으로 Rayleigh Criterion(Godin[1972])에 따라 분조마다 주기 차이에 따른 분석이 가능한 최단기간을 검토하여 실시하였다. 동북아 광역 모델(L1)에서 4개 정점, L1-D1 비교 4개 정점, L1-D2 비교 4개 정점, L1-D3 비교 4개 정점 총 16개 정점(Fig. 4)에 대해 조화분해 후 모델 결과의 검증을 수행하고 광역 실험 결과와 내삽된 상세역 실험 결과를 비교하였다(Table 3).

Fig. 4.

The location of the observed tidal current data used to compare the model results.

Table 3.

Sampling location and observed duration used for harmonic analysis. The Large components are indicated except for the four major substances (M2, S2, K1, O1) in South Korea

검증 결과는 동일 기간 관측 결과와 모델 결과의 조화상수를 이용하여 조류 예측을 수행하였을 때 두 자료의 동방성분과 북방성분의 예측 시계열의 오차를 파악하기 위해 선형회귀를 이용하여 기울기를 파악하였다(Pak and Oh[2010]; Rose and Bhaskaran[2015]; Jeong and Park[2020]). 상관관계(Correlation;R) 및 기울기(slope;b)의 값이 1에 가까울수록 모델 결과의 조화상수가 실제 해역의 흐름을 정확히 재현했다고 판단하였으며, 기울기의 값이 0.7 이하, 1.3 이상일 경우 개선되지 않은 것으로 판단하였다.

3.1 조류 검증 결과 비교

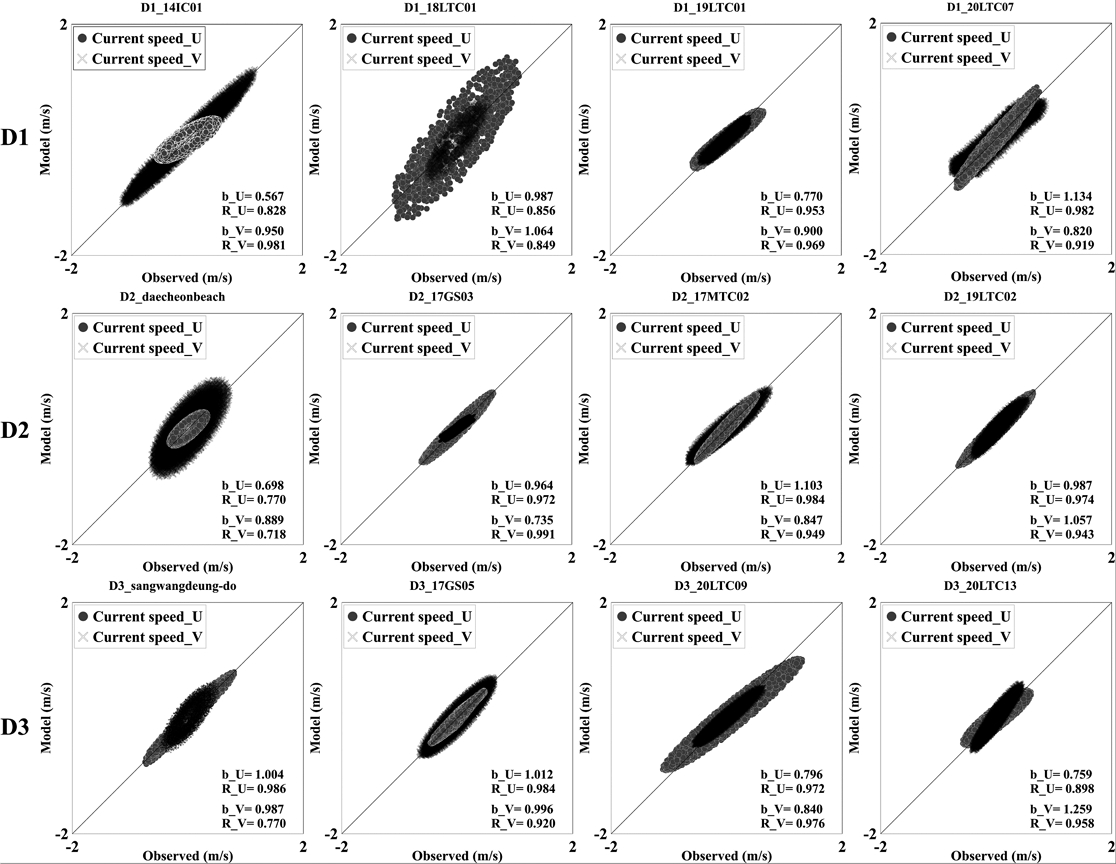
L1 영역은 D1, D2, D3 영역을 모두 포함하나 외해 측 해역에서는 비교할 수 없으므로 분리하여 별도로 모델 정확도를 평가하였으며, 관측값과 모델 예측값을 비교했을 때 연안에 제일 가까운 정점인 20LTC04 정점 결과에서 오차가 크게 발생하였다(Fig. 5). D1 영역은 14IC01에서 상관관계가 0.8 이상으로 나타났지만, 동방 유속성분의 기울기가 0.567로 낮게 나타났다(Fig. 6, D1). D2 영역에서는 대천해수욕장 인근 해양관측부이 동방 유속성분의 기울기가 0.698로 D2 영역에서 가장 부정확하게 예측되었다. 17GS03에서는 북방 유속성분의 기울기가 0.735로 관측 북방유속의 크기가 0.5 m/s 이하로 작아 상대오차가 커진 것으로 판단된다(Fig. 6, D2). D3 해역의 17GS05에서는 b, R값이 1에 가까워 모델 예측값이 관측값을 잘 재현한 것으로 보였지만, 20LTC13의 경우 동방 유속성분과 북방 유속성분의 기울기가 0.759, 1.259로 나타났는데 해당 위치의 경우 섬이 다수 존재하고 지형이 복잡하여 내삽 격자에서도 재현이 미흡한 것으로 판단된다(Fig. 6, D3).

Fig. 5.

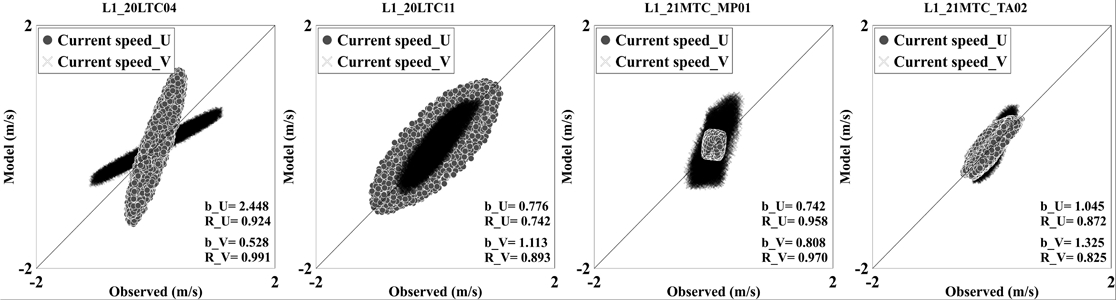
Results of linear regression analysis according to tidal current verification with observation values for the L1 modeling areas.

Fig. 6.

Results of linear regression analysis according to tidal current verification with observation values for the D1, D2, and D3 modeling areas.

3.2 격자해상도 향상에 따른 조류 정확도 개선

동북아 광역 모델 기반의 DB 예측정확도 대비 0.5km로 격자해상도가 개선됨에 따라 실제 연안 인근 예측 결과의 수치상 개선 효과를 보고자 하였다. 이에 따라 L1-D1 20LTC04, L1-D1 19LTC01, L1-D2 17GS03, L1-D3 20LTC09 각 영역 검증 지점을 광역 검증결과와 비교하였다. Fig. 7의 L1-D1 20LTC04와 19LTC01 비교 결과를 보면 동방 유속성분이 모델에서 관측값보다 크게 예측되는 문제가 L1 영역에서 있었지만, D1의 결과에서는 동방 유속성분이 감소하였다. D1 영역에서 L1 영역보다 관측값에 대한 지각 오차가 감소함에 따라 b값의 경우 20LTC04 정점에서 동방 유속성분과 북방 유속성분 모두 2.448→1.117, 0.528→1.021로 크게 개선됨을 확인하였다. L1-D1 19LTC01의 경우에도 기울기가 각각 1.822→0.770, 1.262→0.900으로 L1에 비해 D1에서 크게 개선되었다.

Fig. 7.

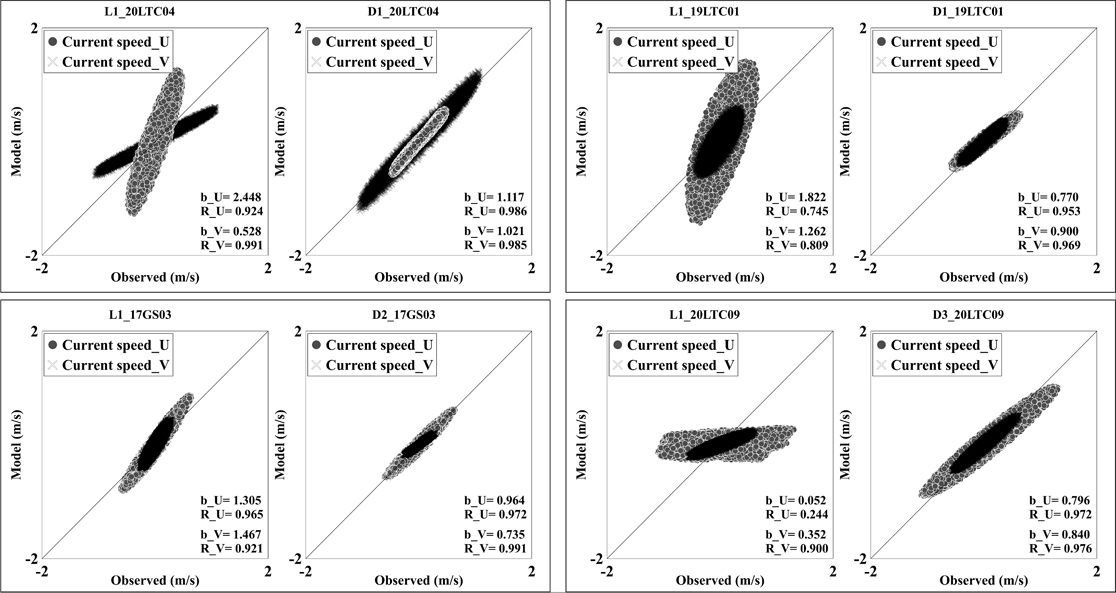
Comparison of tidal current verification results in the existing L1 grid and the D1, D2, and D3 grids.

L1-D2 17GS03의 경우 b값이 1보다 크게 분포하였으나, D2 영역에서 관측값과 유사하게 감소하여 기울기가 0.964, 0.735로 나타났다. L1-D3 20LTC09의 경우는 내삽에 의해 예측정확도가 크게 개선되었다. Fig. 7과 Table 4를 확인해보면 대체로 연안 인근 해안선이 복잡한 경우 기울기 및 상관관계가 1에 근접하게 개선되었음을 알 수 있었다. 이는 내삽된 격자를 이용함에 따라 연안역 인근의 바닥마찰계수와 연직확산계수가 광역과 달리 적용되어 실제 해양환경과 유사해진 것이 1차적인 요인으로 판단되며, 이는 단순히 격자 크기 개선에 따른 결과이기보다는 내삽을 이용한 메커니즘에서 기술적으로 수심별로 다른 마찰계수를 적용할 수 있게 되어 관측값과 유사해진 것이라고 보인다. 과거 연구사례 및 결과를 통해 분석한 Suh[2011] 사례를 살펴보면 천해분조 및 천해역 상세화를 이용하여 예측치의 정확도를 개선하고자 하였다. 연안역에 대해서는 다른 확산계수와 연직확산계수를 적용하여 천해분조의 재연성과 정확도를 증가시켰는데, 연안역 인근 범위에 대해 내삽함에 따라 격자해상도가 증가하였으며 이때 예측모델의 변수를 지역별로 추가한 것과 같은 효과를 거둔 것으로 판단된다.

Table 4.

Comparison of correlation coefficients (R) and slope (b) values using harmonic constituents-based modeling predictions (2021’s) of Wide (L1)-Nesting (D1, D2, D3) grids at KHOA observed locations