딥러닝과 해양환경 연속관측자료를 활용한 저층 용존산소 시간 변동 예측
 ; Sung-Eun Park2, †
; Sung-Eun Park2, † ; Heung Min Kim3
; Heung Min Kim3 ; Suho Bak1
; Suho Bak1 ; Chung-Sook Kim4
; Chung-Sook Kim4 ; Jong Kyu Kim5
; Jong Kyu Kim5 ; Seon-Woong Jang6
; Seon-Woong Jang6
초록
최근 빈산소수괴의 규모와 빈도가 지속적으로 증가하고 있어 양식생물 집단폐사 등 수산업에 심각한 경제적 피해를 발생시키고 있다. 양식 현장에서 빈산소수괴로 인한 피해를 최소화하기 위해서는 빈산소수괴 발생 시기를 사전에 예측하여 조기 대응할 수 있는 예측모델 구축이 필요하다. 본 연구에서는 딥러닝 기반 시계열 예측에 특화된 순환신경망 모델 중 Long Short-Term Memory(LSTM), Gate Recurrent Unit(GRU)과 합성곱 신경망인 1-Dimension Convolution Neural Network(1D-CNN)을 활용하여 저층 용존산소의 변동을 예측한 후 모델별로 성능을 평가하였다. 딥러닝 모델의 입력자료는 당동만 해역에서 2019년부터 2022년 사이에 연속 관측된 층별 해양환경자료를 사용하였다. 2019년과 2021년 자료는 모델의 학습 및 검증자료로 사용하였고 2022년 자료를 예측하여 관측자료와 비교·검증하였다. 모델의 예측 정확도에 영향을 미치는 최적의 입력자료와 매개변수를 선정하기 위해 Pearson 상관관계와 Mutual Information(MI) 분석, 시행착오법을 수행하였다. 그 결과 GRU 모델과 1D-CNN 모델의 성능이 LSTM 모델보다 성능이 우수한 것으로 나타났다. 예측선행시간이 증가할수록 LSTM 모델의 단주기 변동 패턴의 재현성이 감소하였는데, 이는 각 모델 간 구조에 기인한 결과로 나타났다. 본 연구를 통해 시계열 예측에 딥러닝 모델을 적용할 경우 데이터 특성을 반영한 모델을 활용해야 함을 알 수 있었다. 향후 신뢰성 있는 양질의 입력자료 확보와 매개변수 조정을 통해 모델의 예측 오차를 줄일 경우 향상된 예측 정확도와 48시간 이상의 예측시간을 확보할 수 있을 것으로 판단된다.
Abstract
In recent years, the scale and frequency of hypoxia events have continued to increase, causing serious economic damage to the fishery industry, including mass mortality of aquaculture organisms. In order to minimize the damage caused by hypoxia in aquaculture, it is necessary to build a prediction model that can predict the timing of hypoxia in advance and respond to it early. In this study, recurrent neural network models specialized in time series prediction, Long Short-Term Memory(LSTM), Gate Recurrent Unit(GRU), and 1-Dimensional Convolution Neural Network(1D-CNN), a convolutional neural network, were used to predict the variation of bottom dissolved oxygen, and the performance of each model was evaluated. The input data for the deep learning models were layer by layer marine environmental data continuously observed in the Dangdong bay from 2019 to 2022. The 2019 to 2021 data were used as training and validation data for the model, and the 2022 data were predicted and compared and validated with the observed data. Pearson correlation and mutual information(MI) analyses, trial and error methods were performed to select the optimal inputs and parameters that affect the prediction accuracy of the model. The results showed that the GRU model and 1D-CNN model outperformed the LSTM model. The reproducibility of the short-term variation pattern of the LSTM model decreased as the forecast lead time increased, which was attributed to the structure of each model. This study shows that when applying deep learning models to time series forecasting, it is necessary to use models that reflect data characteristics. In the future, if the prediction error of the model is reduced by securing reliable and high-quality inputs and adjusting the parameters, it is expected that improved prediction accuracy and a prediction time of more than 48 hours can be secured.
Keywords:
Hypoxia, Aquaculture, Bottom dissolved oxygen, Deep learning, Prediction키워드:
빈산소, 양식장, 저층 용존산소, 딥러닝, 예측1. 서 론
최근 기후변화, 인구증가와 산업 발달에 따른 과도한 영양염류 유입으로 인해 전 세계적으로 빈산소수괴의 발생 빈도와 강도가 증가하고 있으며, 이는 연안 생태계에 심각한 영향을 미치는 환경 문제 중 하나로 인식되고 있다(Diaz and Rosenberg[2008]; Keeling et al.[2010]; Breitburg et al.[2018]). 일반적으로 해수 중 용존산소 농도가 2 mg/L 이하인 상태를 빈산소라고 정의하는데(Diaz[2001]), 국내에서 빈산소로 인한 폐사는 매년 저층에서 발생하여 주로 피낭류(멍게, 미더덕, 오만둥이), 담치류(홍합) 및 패류(굴) 등의 수하식 양식장에 수산피해를 주고 있다. 연안 양식장에서 용존산소(Dissolved Oxygen)는 양식생물의 성장과 생식주기, 호흡 및 배설 등 대사기능에 영향을 미치는 중요한 지표이다(Pamatmat[1980]; Diaz[2001]). 따라서, 빈산소수괴로 인한 수산업피해를 최소화하기 위해서는 급변하는 양식어장 환경 변화를 파악할 수 있는 해양환경자료의 연속관측 시계열 자료 확보와 빅데이터 분석을 통해 빈산소수괴의 시간변동, 발생 시기 및 확률을 예측할 수 있는 예측 기술이 필요하다.
빈산소수괴 발생 여부에 대한 조사는 주로 선박을 통한 공간분포 조사에 한정되어 있어 명확한 빈산소 발생시기나 해역별 시간변동 특성을 파악할 수 없었다. 용존산소는 조석과 기상의 영향으로 시간 규모의 단주기 변동을 나타내므로 시간에 따른 변화를 볼 수 있는 연속관측이 요구된다. 용존산소의 연속관측은 선박충돌로 인한 기기파손과 생물부착(Biofouling) 등의 문제로 수문학 분야와 비교해서 제한적으로 수행되어 장기간의 자료 확보에 한계가 있었다. 그러나 최근 관측기기와 모니터링 시스템의 발달로 국내·외적으로 장기간 양질의 수질자료 수집이 가능해지면서 관측 자료의 비선형성 등의 다양한 패턴을 분석, 처리할 수 있는 데이터 기반의 인공지능 모델로 용존산소를 예측하는 연구들이 활발하게 수행되고 있다.
과거 시계열 예측은 Autoregressive Integrated Moving Average(ARIMA), Multiple-Linear Regression(MLR)와 같은 데이터 기반의 전통적인 시계열 예측 모델로 용존산소를 예측한 사례가 있었지만, 선형적이고 정규분포를 나타내는 자료에 적합한 기존의 시계열 모델은 비선형 시계열 특성을 가진 용존산소 변동에 대한 신뢰성 있는 예측 결과를 확보하는데 한계가 있었다(Li et al.[2021]; Qin et al.[2019]). 이러한 한계를 극복하기 위해 다양한 환경인자들 사이의 비선형성을 고려할 수 있는 Support Vector Machine(SVM), Artificial Neural Network(ANN), Adaptive Neuro Fuzzy Inference System(ANFIS) 등 머신러닝 기반 모델들을 활용하여 용존산소를 예측하려는 시도들이 있었다(Ahmed[2017]; Ji et al.[2017]). 최근 시계열 자료들의 규모가 커지고 주기도 짧아지면서 딥러닝 기반의 모델들이 시계열 예측 분야에서 전통적인 통계적 모델이나 머신러닝 모델보다 우수한 예측 성능을 나타내는 것으로 보고되었다(Qin[2019]). 특히, 시계열 자료의 장기의존성 문제를 해결하여 연속적인 형식의 자료를 학습하고 예측하는데 탁월한 성능을 지닌 Long Short-Term Memory(LSTM) 모델을 이용하여 용존산소를 예측하는 연구가 활발히 진행되고 있다. LSTM 모델을 적용하여 용존산소를 예측하는 연구는 주로 담수 환경의 하천(Lim et al.[2020]; Zhang et al.[2019]; Kim et al.[2021]; Park and Kim[2021])과 양식장 표층을 대상으로 수행되었다(Huan et al.[2020]; Li et al.[2021]). LSTM 모델을 적용 하여 저층 용존산소를 예측한 연구는 표층에 비교하여 제한적으로 수행되었다(Han et al.[2020]; Park et al.[2022]).
국내를 비롯한 국외에서 딥러닝 기반 용존산소 시간변동 예측 모델이 제시되었으나 대부분 환경이 급변하지 않은 하천이나 담수 환경의 양식장에서 표층 용존산소 예측에 한정되어 있었다. 저층 용존산소의 시간변동을 예측한 연구도 제한적으로 수행되었지만 6시간 이하의 단기 예측에 한정되어 다양한 선행예보시간에 따른 예측 정확도 분석에 관한 연구가 부족하였다. 또한, 성층의 강화로 빈산소가 강해지는 시기인 7~9월 기간에 대한 예측과 수일~수십일간 빈산소가 지속되는 구간 및 불규칙적으로 변동하는 구간에 대한 예측연구가 수행되지 않았다. 빈산소수괴는 수하식 양식생물의 대량폐사를 일으킬 수 있기 때문에 양식어업 현장에서 수산 피해를 최소화하기 위해서는 빈산소수괴의 생성, 지속, 소멸 시기를 포함하는 장기변동 예측과 단주기 변동 예측 연구가 필요하다. 빈산소수괴 발생현황은 주로 현장조사 이후 속보를 발효하는 방식으로 수행되고 있으며, 이러한 사후 대응 방식은 빈산소 발생시기 정보를 신속하게 제공할 수 없다는 한계가 있다.
따라서 본 연구에서는 연속관측 자료와 딥러닝 기반 모델을 이용하여 당동만 해역 저층 용존산소의 시간변동을 예측하고자 하였다. 이를 위해, 최근 시계열 예측에 주로 활용되는 딥러닝 기반의 순환신경망 모델 중 수질예측에 활발하게 활용되고 있는 LSTM 모델과 GRU 모델, 자료의 특징을 추출할 수 있는 CNN 기반의 1D-CNN 모델을 활용하였다. 모델의 예측 방법은 Pearson 상관분석과 MI(Mutual Information) 분석을 통해 최적의 입력자료를 선정하고 시행착오법(Trial and errors method) 통해 딥러닝 모델의 최적 매개변수(Optimal hyper-parameters)를 탐색하였다. 모델의 선행예측시간은 1~72시간으로 설정하여 저층 용존산소 시간변동을 예측하고 그 정확도를 모델별로 비교·평가하였다.
2. 재료 및 방법
2.1 연구대상해역
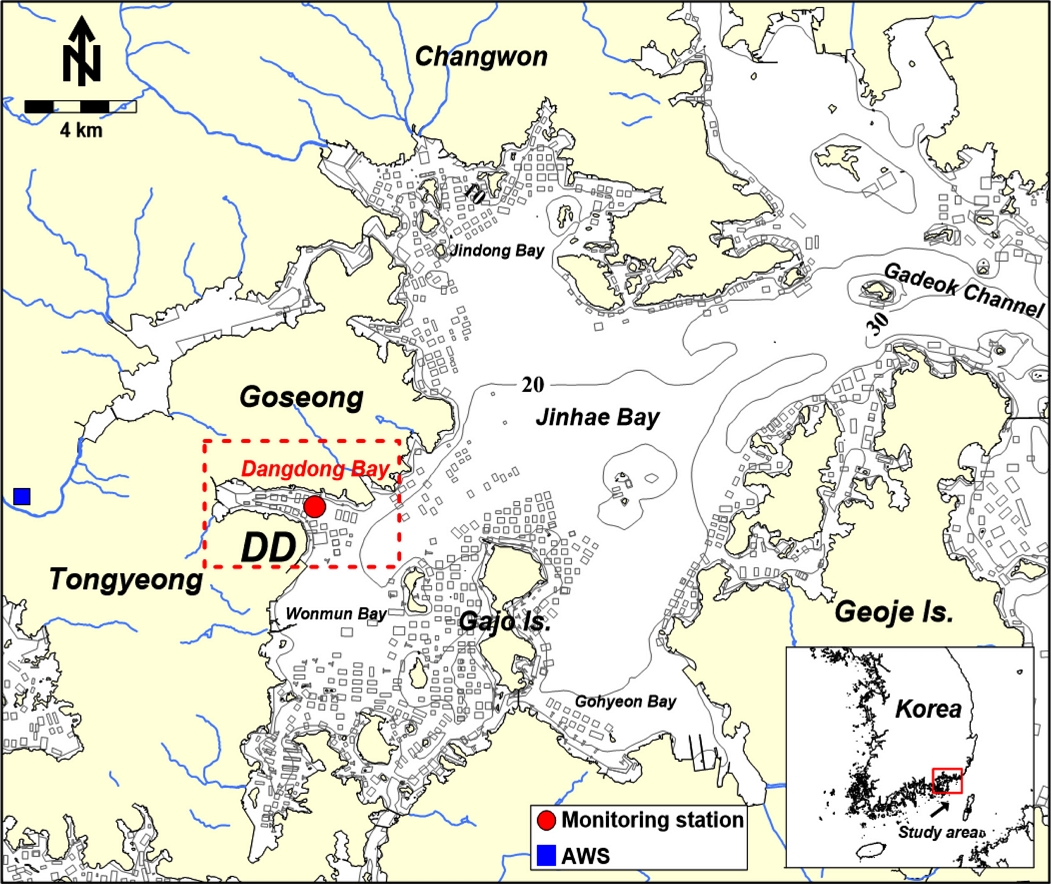
당동만은 진해만 서북부에 위치한 반폐쇄성 소규모만이며, 만 주변에는 다양한 산업단지가 조성되어 있고 만 내에는 수하식 굴 양식장이 밀집되어 있다. 당동만은 외해와 해수교환이 원활하지 않은 지리적인 특성과 주변 산업단지와 양식장으로부터 유기물 유입이 증가하면서 부영양화가 가속화되고 있으며, 이로 인해 매년 여름철 빈산소수괴가 형성되어 저서생물을 포함하여 양식생물에 악영향을 미치고 있다.
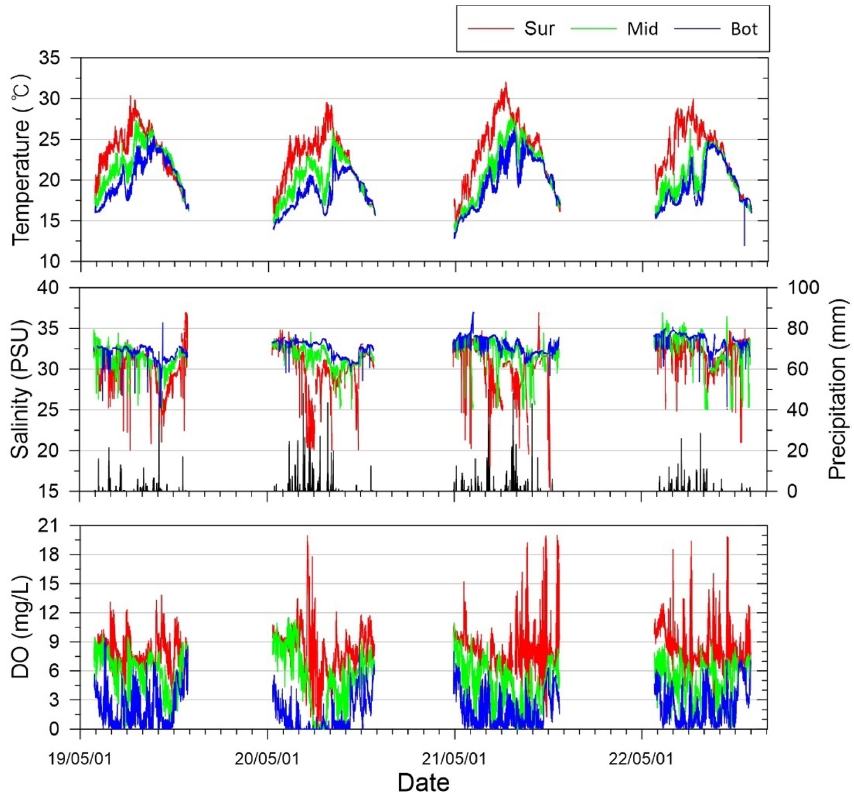
본 연구에서 사용한 딥러닝 모델의 입력 및 검증자료는 국립수산과학원 해양환경연구과에서 2019년 4월부터 2022년까지 11월까지 약 4년간 당동만 관측정점에서 1시간 간격으로 연속관측된 층별(표, 중, 저층) 수온, 염분 및 용존산소를 사용하였다(Fig. 1). 딥러닝 모델 적용시 자료의 품질은 모델의 학습과 결과의 신뢰도에 영향을 미치므로 자료의 품질 향상을 위한 전처리 과정이 요구된다. 연안에서는 외해와 달리 생물부착이나 선박충돌로 인한 파손 등의 문제로 센서 정확도가 감소하거나 결측자료가 존재하게 된다. 당동만에 관측된 시계열 그래프와 결측자료의 항목별 통계자료 및 결측 비율을 Fig. 2와 Table 1에 각각 제시하였다. 4년간 당동만 해역에서 관측된 층별 수온과 용존산소의 결측 비율은 0.97~1.95%, 결측 시간은 최대 101시간으로 나타났다. 염분의 결측 비율은 3.03~4.04%, 결측 시간은 최대 264시간으로 가장 높게 나타났다. Fig. 2와 같이 층별 염분의 자료의 결측이 되지 않더라도 센서 감도의 문제로 층별 염분이 역전되거나 강우에 상관없이 염분 값이 감소하는 경우가 존재하였다. 딥러닝 모델 학습시 이러한 불확실한 데이터를 포함하는 것은 데이터 기반의 모델에 상당한 오류를 도입할 수 있으며, 잘못된 결과를 도출할 수 있다. 따라서 염분자료는 불안정한 데이터가 다수 존재하여 본 연구에서는 입력자료로 활용하지 않았다. 한편, 원시데이터(Raw data)만으로 모델을 설계할 경우, 모델이 설명할 수 있는 부분은 한계가 있기 때문에 파생변수 생성이 요구된다. 따라서 본 연구에서는 층별 수온과 용존산소와 더불어 저층 용존산소 변동과 관련성이 높은 표층 수온과 저층 수온차 △T(Kang et al.[2020]; Lee et al.[2017])를 파생변수로 추가하였고 시계열 자료의 변동성을 입력자료로 활용하기 위해 저층 용존산소와 △T의 1차 차분 자료도 파생변수로 활용하였다. 차분(Differencing)은 연속된 시계열 데이터 간의 차이를 계산하는 통계적 기법으로, 1차 차분은 현재 시점의 값에서 바로 이전 시점의 값의 차이를 구하는 것이다. 1차 차분 자료를 입력자료로 활용하는 목적은 시계열 데이터에서 추세를 제거하고 변동성을 반영함으로써, 딥러닝 모델이 데이터 패턴을 더욱 효과적으로 학습하고 단기적인 변화량을 예측할 수 있도록 하기 위함이다. 저층 용존산소는 기상과 조석에 따라 변동하는 특성을 나타내므로 당동만 인근 고성 AWS의 기온, 바람, 강수량 자료를 수집하였다. 본 연구에서는 2019년부터 2021년의 자료를 모델의 학습 자료로 활용하고 2022년는 검증자료로 활용하였다.
2.2 입력변수 설정
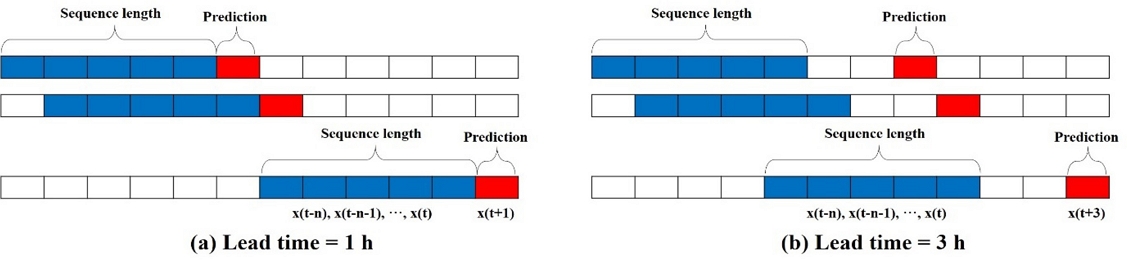
특성 선택(Feature selection)은 예측모델의 효율성과 정확도에 영향을 미치는 중요한 전처리 과정 중 하나이다. 다양한 변수를 모델 학습에 적용하기 전에 종속 변수에 영향을 미치는 각 독립변수를 선정하여 입력자료로 활용하면 예측모델의 성능을 향상시킬 수 있다. 종속변수와 독립변수들 사이의 상관성을 파악하기 위해 피어슨 상관분석(Pearson correlation analysis)이 주로 활용되고 있다. 피어슨 상관분석은 독립 변수 간에 어떤 선형적 관계를 있는지를 분석하는 방법이며, 상관계수 r은 -1에서 +1까지의 값을 가진다. 그러나 전술한 방법은 종속변수와 독립변수들 사이에서 선형적인 관계를 나타낼 때 적합하며(Zhang et al.[2019]), 연안에서 각각의 변수들은 서로 비선형적인 관계를 나타내므로 이러한 특성을 반영할 수 있는 상관성 파악이 요구된다. MI 분석은 선형적인 관계뿐만 아니라 비선형성 변수들 간의 중요도를 평가하고 모델링에 사용할 변수 파악이 가능한 특성 선택 방법으로 수질항목을 예측할 시 활용되고 있다(Zhang et al.[2019]; Iskandaryan et al.[2022]). 본 연구에서는 python 프로그램을 이용하여 피어슨 상관분석과 MI 분석을 수행하였다. 시계열 예측에서 데이터를 연속적으로 인식하기 위해 슬라이딩 윈도우 기법(Sliding window)을 적용하였으며, 모델의 학습 시 입력 데이터의 길이를 조정하는 시퀀스 길이(Sequence length)는 24시간으로 설정하였다. 즉, 과거 24시간(t-23 ~ t)를 활용하여 n시간 후의 값(t+n)을 예측하도록 설정하였다. Fig. 3은 lead time이 1 h과 3 h 이후 저층 용존산소를 예측할 수 있도록 구성된 학습 과정을 보여준다. 비교하는 과정을 반복하여 n일 이후 저층 용존산소를 예측하는 모델을 생성할 수 있도록 입력자료를 구성하였다.
한편, 각 변수들은 서로 다른 단위와 범위를 가지므로 이를 동일하게 조정하는 과정이 필요하다. 수집한 변수들은 최대값을 1, 최소값을 0으로 설정하는 최소-최대 표준화(Min-Max scaling)을 통한 정규화(Normalization)로 데이터 전처리를 수행하였으며, 식 (1)과 같이 표현된다.
| (1) |
2.3 딥러닝 기반 시계열 모델
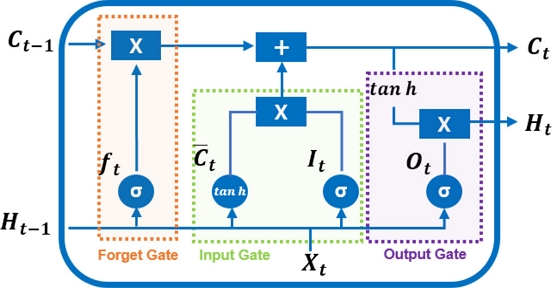
본 연구에서는 저층 용존산소 시계열 변동을 예측하기 위해 LSTM, GRU, 1D-CNN 모델을 활용하였다. Long Short-Term Memory(LSTM)은 RNN 모델에서 발생하는 장기의존성(Long-term dependency) 문제를 해결하기 위해 은닉층에 셀 상태(Cell state, Ct) 구조를 추가한 모델이다(Hochreiter and Schmidhuber[1997]). LSTM 모델의 구조는 Fig. 4와 같이 망각게이트(Forget gate, ft), 입력게이트(Input gate, it), 그리고 출력게이트(Output gate, ot)로 구성되어 있다. 망각게이트(ft)는 이전의 정보를 버릴지 결정하는 과정으로 식 (2)와 같이 이전 hidden state(ht-1)와 현재 입력값 xt를 연산하고 0과 1사이의 값을 출력하는 sigmoid 함수를 적용한다. 0에 가까울수록 이전 정보를 저장하지 않겠다는 의미이고, 1에 가까울수록 이전 정보를 보존하겠다는 의미이다. 여기서, σ는 sigmoid 함수, Wt는 망각게이트의 가중치, ht-1은 이전값의 출력값, xt는 현재 입력값, bf는 편향을 의미한다.
| (2) |
입력게이트(it)는 어떤 새로운 정보를 cell state(Ct)에 저장 또는 추가할 것인지를 결정하게 되는데 이는 크게 다음과 같은 두 단계로 구분된다. 먼저 식 (3)과 같이 시그모이드 함수를 이용하여 업데이트할 자료를 결정하며, 식 (4)와 같이 하이퍼볼릭 탄젠트 함수(tanh)를 통해 cell state에 추가될 수 있는 새로운 후보 값 Ct 벡터를 만들게 된다. 여기서, Wi, Wc는 각각 입력게이트 및 후보 셀의 가중치, bi, bc는 입력게이트와 후보 셀의 편향을 나타낸다.
| (3) |
| (4) |
다음으로 장기 상태라 불리는 cell state(Ct)에서는 식 (5)과 같이 이전 cell state(Ct-1)와 망각게이트(ft)를 통해 이전 시점의 정보를 얼마나 반영할지, 후보 Ct와 입력게이트(it)를 통해 현재 시점의 정보를 얼마나 반영할지 계산한다. 계산된 값들을 더해 현재 시점의 새로운 cell state(Ct)를 업데이트하게 된다.
| (5) |
마지막으로 출력게이트 ot는 식 (6)과 같이 시그모이드 함수를 이용해서 현재 cell state(Ct)를 얼마나 출력하고자 하는지 결정하고, 식 (7)과 같이 하이퍼볼릭 탄젠트 함수(tanh)를 이용하여 활성화된 cell state(Ct)와 연산을 통해 hidden state(ht)를 최종적으로 출력하게 된다.
| (6) |
| (7) |
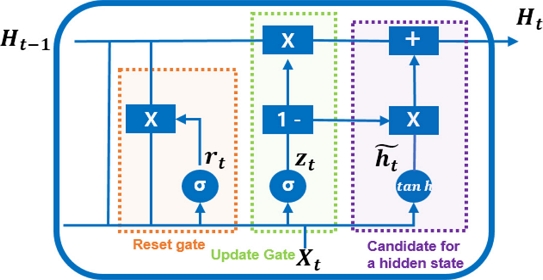
Gate Recurrent Unit(GRU)는 LSTM의 변형 알고리즘으로(Cho et al.[2014]), LSTM의 망각게이트(forget gate), 입력게이트(input gate)와 유사한 역할을 하는 업데이트 게이트(Update gate, zt)와 리셋 게이트(Reset gate, rt)로 구성되어 있다(Fig. 5). 또한, cell state와 hidden state를 합쳐 하나의 hidden state로 표현하나 LSTM과 동일하게 장기기억 특성을 가지고 있다. 리셋 게이트(rt)는 이전의 정보를 얼마만큼 전달할지 결정하며, 업데이트 게이트(zt)는 과거와 현재의 정보를 얼마나 반영할지를 결정한다. 이에 대한 수식은 식 (8)~(10)과 같다. 식(10)과 같이 리셋 게이트(rt)는 하이퍼볼릭 탄젠트 함수(tanh)와 연산을 통해 hidden state에 추가될 수 있는 새로운 후보 값 ht 벡터를 만들게 된다. 식 (11)에서 1- zt는 이전 정보의 반영 비율을 결정하는 forget gate 기능을 하며, zt는 현재 정보의 반영 비율을 결정하는 input gate 역할을 한다. 즉, 이전 hidden state(ht-1)와 (1-zt)를 통해 이전 시점의 정보를 얼마나 반영할지 계산하고, 후보 ht 와 업데이트 게이트(zt)를 통해 현재 시점의 정보를 얼마나 반영할지 계산한다. 계산된 값들을 더해 새로운 hidden state(ht)를 업데이트하게 된다. 여기서, xt는 현재 입력값, ht는 현재 출력값, rt는 리셋 게이트, zt는 업데이트 게이트, W는 가중치, σ는 sigmoid 함수를 의미한다. GRU는 LSTM보다 게이트 수가 적어 구조적으로 더 간단한 모델이다. 예측성능은 LSTM 모델에 비해 우월하다고 할 수 없지만 학습할 매개변수와 가중치가 적어 학습 속도가 빠르다는 장점이 있다(Li et al.[2021]).
| (8) |
| (9) |
| (10) |
| (11) |
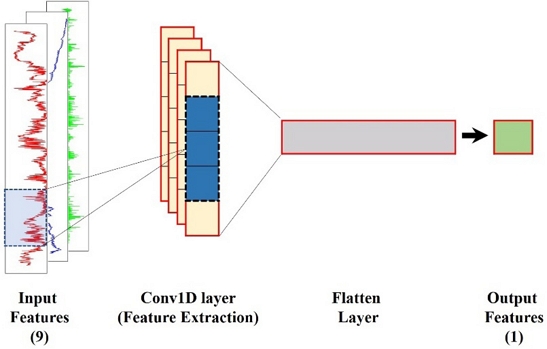
Convolutional Neural Network(CNN)은 딥러닝 알고리즘의 한 종류로 이미지와 영상과 같은 격자 형태로 배열된 2D 데이터의 패턴을 식별하는 것에 특화되어 있는 신경망이다. CNN은 공유 매개변수가 있는 다수의 필터를 활용하여 2차원 데이터의 공간 정보를 유지함으로써 이미지 내 인접 영역의 특징을 효율적으로 추출하고 학습한다. 주로 이미지 처리에 사용하는 2D-CNN과 다르게 1D-CNN은 자연어 처리와 시계열에서 사용되며 커널을 시간 방향으로 움직이면서 Feature를 추출한다(Fig. 6). 1D-CNN 층은 데이터에 내재된 특징을 추출하는 역할을 하게 되는데 필터의 개수는 얼마나 많은 윈도우를 학습할지 결정하며 이는 출력 공간의 차원과 일치하게 된다. 즉, 필터를 한 개만 쓰게 되면 1D-CNN 모델이 첫 번째 합성곱 층에서 하나의 단일 기능만을 학습하게 되고 이는 입력 데이터 사이 연관성이나 복잡성을 측정하기에 부족할 수 있다(Azizjon et al.[2020]). 커널 사이즈는 합성곱 창의 높이를 뜻하며 너무 작으면 과소적합을 일으키고, 너무 크다면 과대적합을 일으킬 수 있다.
2.4 딥러닝 모델 입력 파라미터
딥러닝 모델은 입력자료와 더불어 모델의 하이퍼파라미터(Hyper-parameter)의 조합에 따라 예측 성능이 달라지기 때문에 학습 전 최적의 매개변수 선정과정이 필요하다. 하이퍼파라미터는 값이 클수록 자료의 복잡성을 학습하는데 유리하지만, 과적합(Overfitting) 문제가 발생할 수 있기 때문에 적절한 값을 설정하는 것이 매우 중요하다. 최적의 하이퍼파라미터를 찾기 위한 방법은 과학적인 접근보다 주로 사용자의 경험이나 시행착오(Trial and errors)에 의존하여 설정되고 있다. 본 연구에서 설정한 최적의 하이퍼파라미터는 시행착오법을 통해 설정하였으며, 이를 Table 2와 Table 3에 제시하였다. 딥러닝 모델의 은닉층은 1개의 Layer로 구성하였으며, 유닛은 각각 64로 설정하였다. 활성화 함수는 비선형성을 고려할 수 있는 tanh 함수를 사용하였으며, 완전연결층(Fully connected)의 활성화 함수는 linear로 설정하였다. 최적화를 위한 손실함수는 평균제곱오차(Mean Squared Error, MSE)를 사용하였으며, 최적화 함수로는 Adam으로 설정하였고 learning rate를 0.0001로 설정하였다. 과적합을 방지하기 위해 dropout을 적용하였으며, 그 값은 0.2로 설정하였다. Batch size는 64, epoch는 100으로 설정하였고 학습의 과적합을 방지하기 위해 Early Stopping 기법을 적용하여 검증 데이터가 15회 이후까지 학습을 진행하였을 때 오차가 개선되지 않는 경우 자동으로 훈련을 종료하도록 설정하였다.
2.5 모델 성능평가지표
본 연구에서는 모델별 성능을 비교하기 위해 상관계수(Correlation Coefficient, CC), 결정계수(Coefficient of determination, R2), 평균절대오차(Mean Absolute Error, MAE), 평균제곱오차(Mean Square Error, MSE), 제곱근평균제곱오차(Root Mean Square Error, RMSE)를 모델 평가지수로 산정하였으며, 이는 식 (12)~(16)과 같다. 상관계수(CC)는 관측과 예측 데이터의 공분산을 각 데이터 분산의 내적으로 나눈 결과로 -1부터 1 범위의 값을 도출하며, 0에 가까울수록 상관성이 없고 1에 가까울수록 예측값이 관측값과 강한 양의 상관관계가 있다는 의미이다. R2은 0과 1사이의 값을 가지며, 1에 근접할수록 모델의 성능이 높다고 해석할 수 있다. MAE는 예측값과 관측값의 차이의 절대값을 평균한 값이다. MAE는 절대값을 취하기 때문에 오차의 크기를 그대로 반영한다. MSE는 예측값과 관측값의 차이의 제곱한 값의 평균을 의미하며, 특이값이 존재하면 수치가 많이 늘어난다는 특징을 지니고 있다. 이를 보완하고자 MSE에 제곱근(Root) 씌운 값이 RMSE이다. MAE, MSE 및 RMSE는 0에 가까울수록 예측 모델의 정확도가 높다고 해석할 수 있다.
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
- 여기서 Ot = 관측값
- Ot = 관측값의 평균
- Pt = 관측값
- Ot = 관측값
- N = 데이터 개수
3. 결과 및 고찰
3.1 상관관계 분석
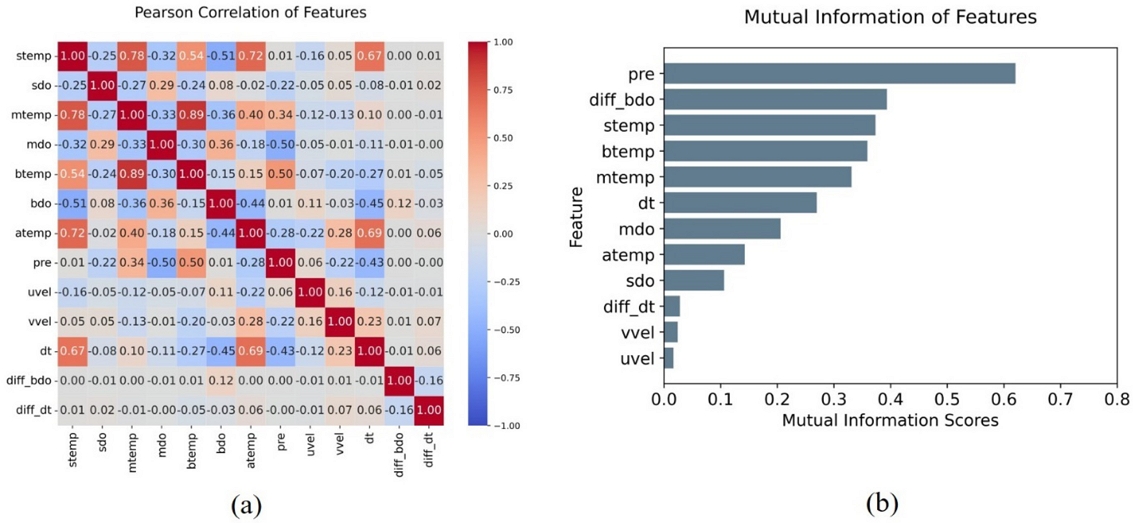
본 연구에서는 Pearson 상관분석과 MI 분석을 통해 저층 용존산소에 영향을 미치는 요인을 파악하였다(Fig. 7). Pearson 상관분석 분석결과, 표층 수온이 저층 용존산소와 -0.51의 상관관계를 나타내며 가장 큰 영향을 미치는 요인으로 나타났다. 이어서 표층 수온과 저층 수온의 차이를 나타내는 △T는 -0.45를 보였고, 기온(-0.44), 중층 수온(-0.36), 중층 용존산소(-0.36) 순으로 상관관계가 높았다. MI 분석을 통해 저층 용존산소와 가장 높은 정보량을 공유하는 변수를 분석한 결과, 누적강우량이 저층 용존산소와 0.62의 MI 값을 나타내며 가장 높은 정보량을 공유하는 것으로 나타났다. 이어서 저층 용존산소 1차 차분(0.39), 층별 수온, △T(0.27) 순으로 MI 값이 높았다. 각 통계 분석을 통해 추출된 입력변수를 활용하여 모델을 예측한 결과, Pearson 상관분석과 MI 분석을 통해 파악된 변수 9개(층별 수온, 중층 용존산소, 저층 용존산소, 기온, 누적강우량, △T, 저층 용존산소 1차 차분)를 모두 활용하는 것이 예측성능이 높은 것으로 나타나 9개 변수를 활용하여 예측선행시간에 따른 모델간 정확도를 비교, 분석하였다.
3.2 예측성능 비교
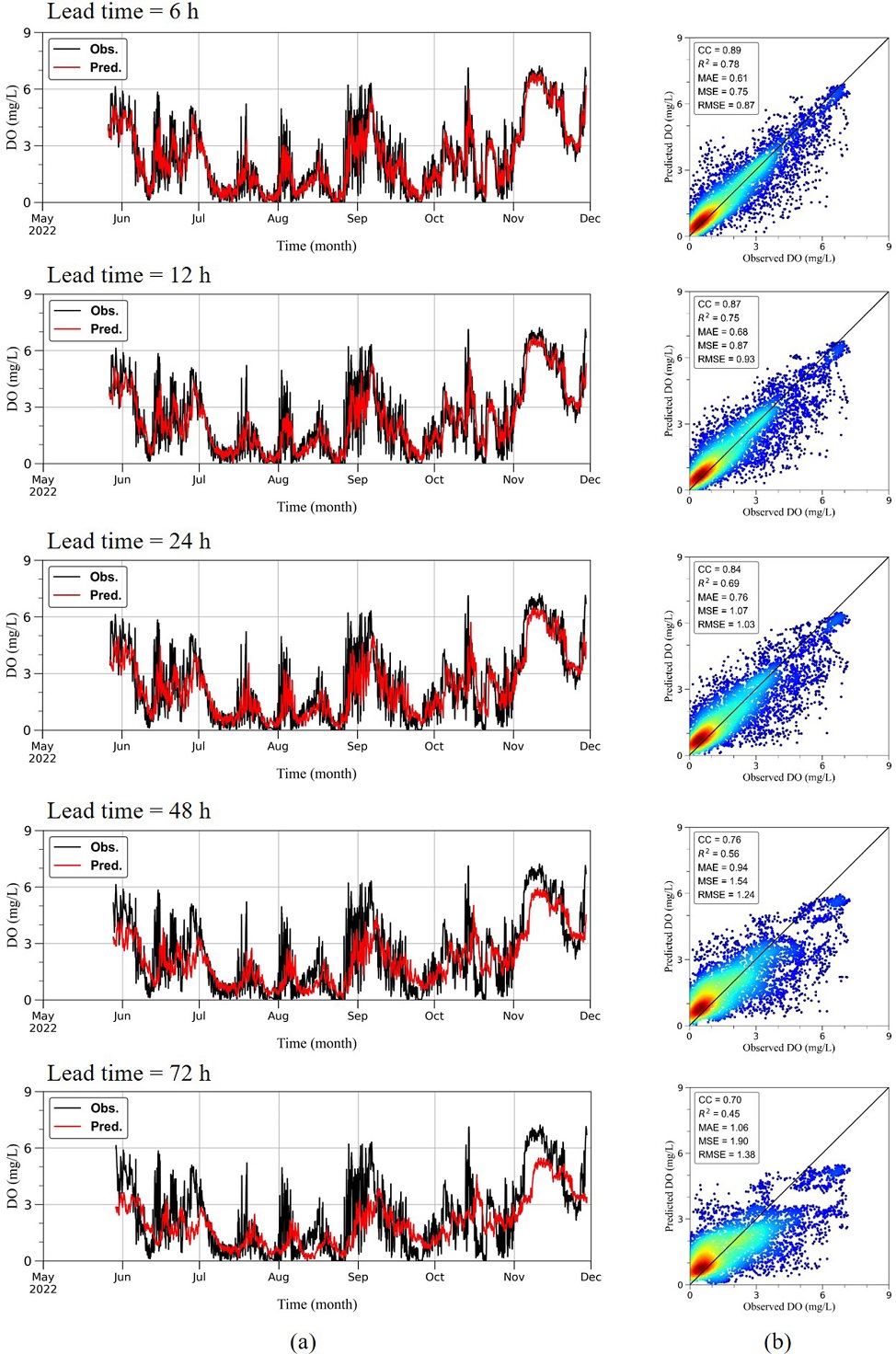
본 연구에서는 앞에서 언급한 상관분석을 통해 선정된 9개 변수를 입력자료로 활용하여 순환신경망 계열의 LSTM, GRU 모델과 합성곱 신경망 계열의 1D-CNN 모델로 용존산소의 시간 변동을 예측하였다. 예측결과를 정량적으로 평가하기 위해 5가지 성능평가지표를 산정하여 모델별로 비교하였으며, 예측선행시간은 1~72시간까지 설정하여 Fig. 8와 Table 4에 제시하였다. 딥러닝 모델 모두 예측선행시간이 길어질수록 예측 정확도가 감소하는 것으로 나타났으며, 1D-CNN 모델의 예측성능이 가장 우수한 것으로 나타났다. 예측선행시간이 증가함에 따라 LSTM 모델의 CC는 0.97에서 0.62, R2는 0.94에서 0.38으로 감소하였으며, MSE는 0.19에서 2.15 mg/L, RMSE는 0.44에서 1.47 mg/L, MAE는 0.29에서 1.20 mg/L로 증가하였다. GRU 모델의 CC는 0.97에서 0.70, R2는 0.95에서 0.45로 감소하였으며, MSE는 0.19에서 1.89 mg/L, RMSE는 0.44에서 1.37 mg/L, MAE는 0.28에서 1.06 mg/L로 예측오차가 증가하였다. 1D-CNN 모델의 CC는 0.97에서 0.70, R2는 0.95에서 0.45으로 감소하였으며, MSE는 0.19에서 1.90 mg/L, RMSE는 0.43에서 1.38 mg/L, MAE는 0.28에서 1.06 mg/L로 예측오차가 증가하였다. Moriasi et al.[2015]에 따르면 수질 예측모델 모의에 대해 R2 ≥ 0.80이면 "Very Good"으로, 0.70 ≤ R2<0.80이면 "Good"으로, 0.50 ≤ R2<0.70이면 "Satisfactory", R2<0.50이면 "Not-satisfactory"와 같은 기준을 제시하고 있다. 본 연구에서의 예측선행시간 48시간까지에 대한 결과는 모두 "satisfactory"로 딥러닝 모델을 활용한 저층 용존산소 시간변동 예측이 예측선행시간 48시간까지는 안정적으로 모의할 수 있다는 것을 보여준다.
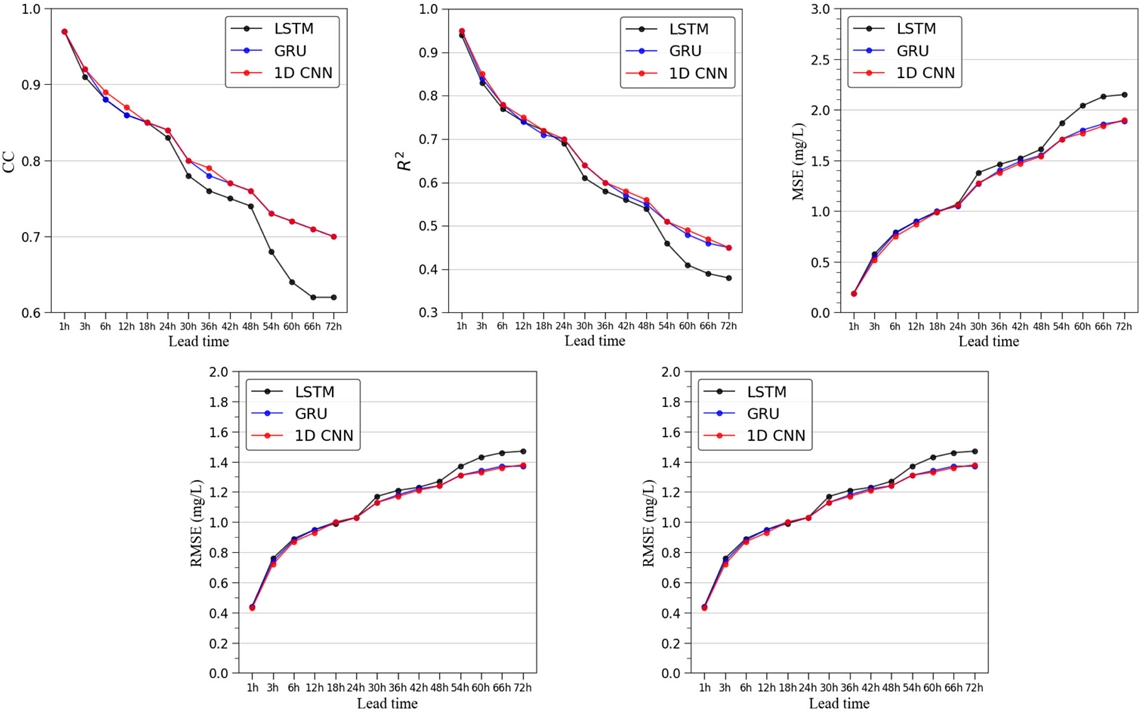
Comparison of the evaluation indexes LSTM, GRU, and 1D-CNN model under different prediction time(1-72 hours).

Evaluation results of predictive performance using five error indicators for 1 to 72 h of prediction time.
각 모델별로 5개의 예측선행시간(6, 12, 24, 48, 72 시간)에 따른 예측 결과와 관측자료의 시계열 그래프와 산점도를 Fig. 9~11에 나타내었다. 시계열 자료에서 볼 수 있듯이, 예측선행시간이 증가할수록 GRU와 1D-CNN 모델이 LSTM 모델보다 단주기 변동성을 더 잘 모의하는 것으로 나타났다. 모든 모델에서 예측선행시간 24까지 관측자료의 시간에 따른 변동성을 유사하게 모의하였으나 그 이후는 GRU 모델과 1D-CNN 모델이 LSTM 모델보다 저층 용존산소의 단주기 변동을 더 잘 재현하는 것으로 나타났다.
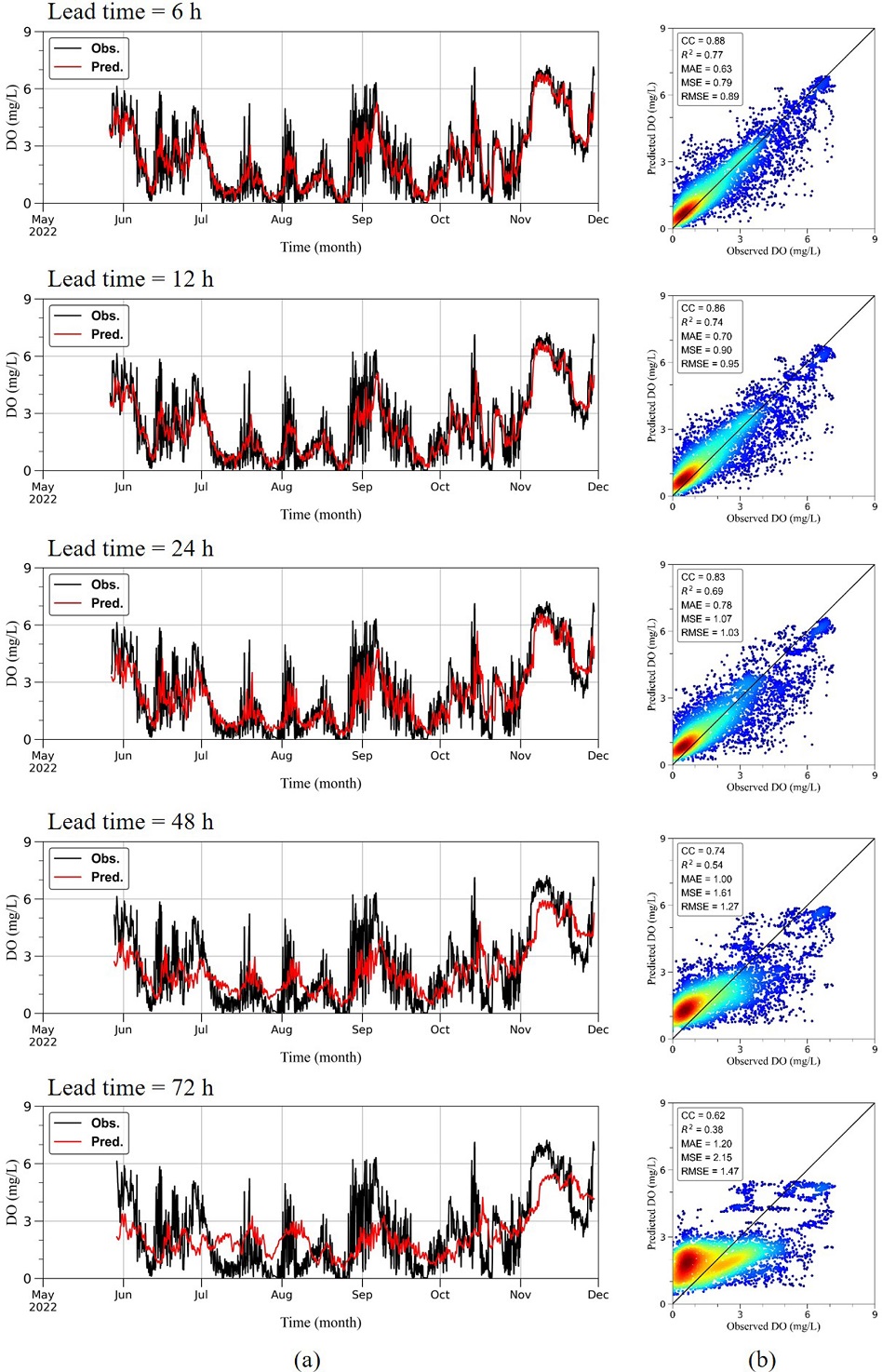
Result of LSTM to predict bottom dissolved oxygen in Dangdong bay by training with 3 years data(2019 to 2021). (a) Timeseries of 6 to 72 h prediction. (b) Scatterplot of 6 to 72 h prediction.
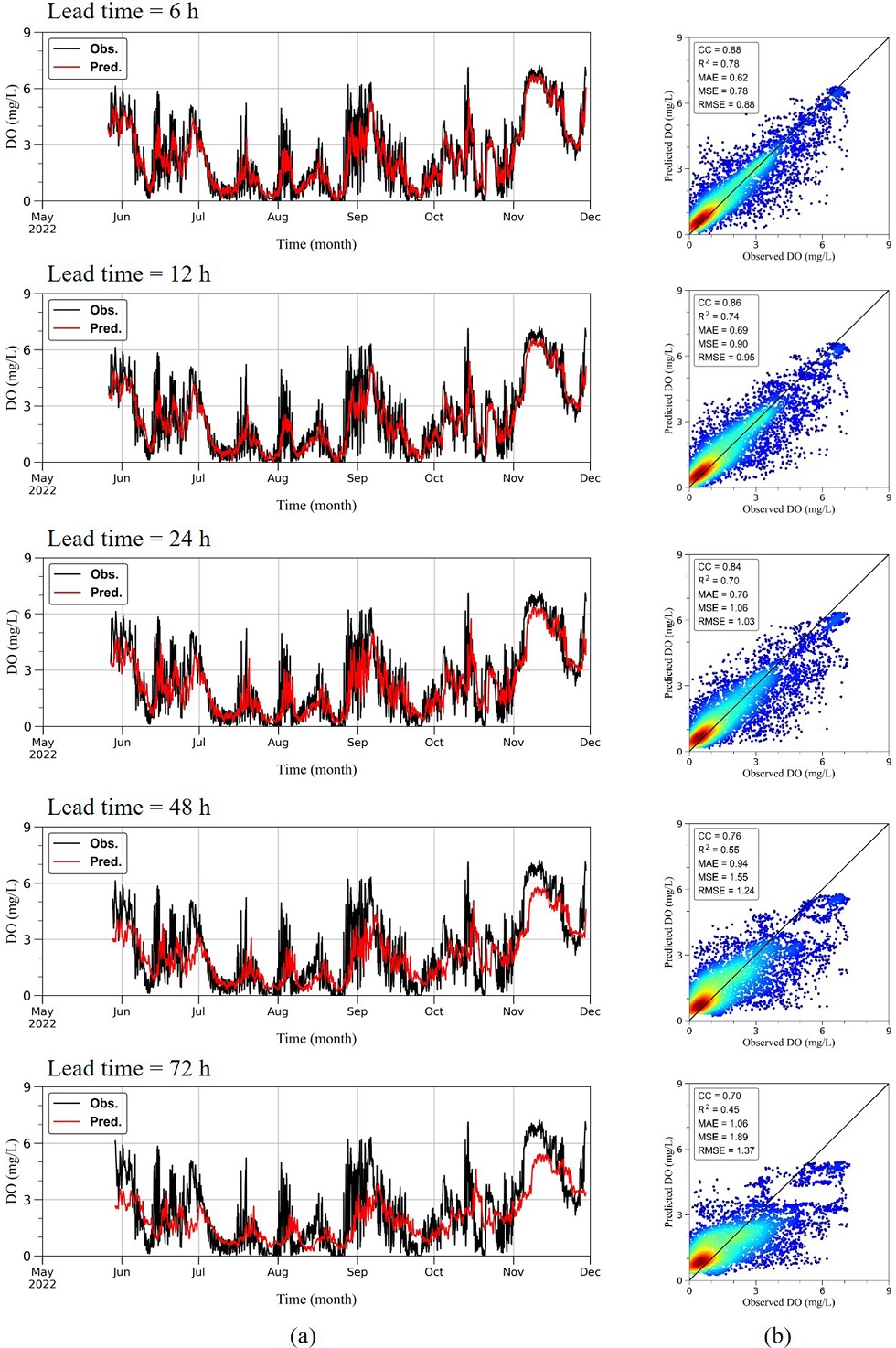
Result of GRU to predict bottom dissolved oxygen in Dangdong bay by training with 3 years data(2019 to 2021). (a) Timeseries of 6 to 72 h prediction. (b) Scatterplot of 6 to 72 h prediction.
3.3 모델 구조에 기인한 예측 성능 비교
각 모델에 따른 예측성능의 차이는 근소하였지만 시계열 변동 패턴을 통한 정성적 평가에서는 GRU와 1D-CNN 모델이 LSTM 모델보다 장주기 성분뿐만 아니라 단주기 변동의 재현성이 높은 것으로 나타났다. 특히, 순환신경망 계열인 LSTM 모델과 GRU 모델의 성능 차이는 두 모델간의 구조적 차이에 기인한 결과로 판단된다. LSTM 모델은 앞서 언급한 바와 같이 input gate, forget gate, cell gate로 구성되어 있는데, forget gate에서는 이전 시점의 hidden state와 현재 시점의 input에 대한 연산을 진행하고 활성화 함수로 sigmoid 함수를 사용하게 된다. Sigmoid 함수는 0~1사이의 값을 출력하게 되는데, 0에 가까울수록 이전 정보를 잊는 것을 의미하며 1에 가까울수록 이전 정보를 기억하는 것을 의미한다. 즉, forget gate는 이전에 입력된 자료를 얼마나 기억하여 모델에 반영할지 결정하는 요소로 모델이 장기 기억을 유지할 수 있도록 하는 핵심 역할을 하게 된다. 시계열 데이터에서 대표적인 장기 성분은 추세 성분(Trend)과 계절 성분(Seasonal)이다. LSTM 모델은 시계열 자료의 trend와 seasonal 성분 같은 주기가 뚜렷하거나 장주기 성분에 대한 정보를 잘 반영할 수 있어도 본 연구의 저층 용존산소 자료처럼 단주기 변동이 강한 자료의 경우 forget gate의 sigmoid 함수에 의해 정보가 삭제되어 예측 시간(Lead time)이 길어질수록 LSTM 모델의 성능이 감소한 것으로 판단된다.
GRU 모델은 LSTM 모델보다 간소화된 2개의 gate(reset, update)를 사용하여 파라미터 수가 적어 학습이 빠르고 예측성능도 LSTM 모델과 유사하거나 높다고 알려져 있다(Chung et al.[2014]). GRU 모델의 update gate는 LSTM 모델의 input gate와 forget gate의 기능을 수행한다. Update gate는 단기 정보와 장기 정보사이의 균형을 조절하여 필요한 정보를 유지하거나 불필요한 정보를 잊는다. 여기서 tanh 함수를 사용하여 이전 시점 정보의 보존 정도를 조절한다. 예를 들어 tanh가 0일 경우 이전 시점의 정보를 거의 유지하지 않지만 이전 시점의 정보를 완전히 잊지는 않게 된다. 반면, reset gate는 과거 정보를 얼마나 무시할지 결정하는데, 이는 모델이 과거 상태를 완전히 무시하고 새로운 입력 정보에만 집중할 수 있게 함으로써 단주기 시계열 정보를 빠르게 반영할 수 있는 역할을 수행한다. 이러한 모델 구조로 인해 단주기 변동이 강한 시계열 자료의 경우는 GRU 모델이 LSTM 모델보다 성능이 좋은 것으로 판단된다.
합성곱 신경망 계열인 1D-CNN 모델은 일반적으로 이미지를 분석하는 데 사용되는 2D-CNN의 원리를 변형하여 시계열 데이터에 적용한 것으로, 합성곱 층을 통해 시계열 데이터 내의 지역적 패턴을 효과적으로 탐지하고 분석하게 된다. 각 합성곱 층은 입력 데이터의 작은 구간을 순차적으로 살펴보며, 다양한 필터(또는 커널)를 적용하여 해당 구간의 특징을 추출하게 된다. 1D-CNN은 슬라이딩 윈도우 방식을 활용해 데이터의 지역적으로 변화하는 패턴을 신속하게 감지하고, 이를 통해 보다 정확한 예측을 가능하게 한다. 특히, 시계열 데이터에서 단기적 변화나 주기성이 두드러지는 특성을 파악하는데 매우 유용하며, 이러한 특성으로 인해 단기 변동성이 강한 시계열 데이터를 처리할 때 1D-CNN이 뛰어난 성능을 보이는 것으로 보고되었다(Shin et al.[2021]). 따라서 향후 단기 변동성이 큰 저층 용존산소와 같은 시계열 자료를 예측할 때, LSTM 모델보다는 예측 성능이 우수한 GRU 모델이나 1D-CNN 모델을 사용하는 것이 더 합리적이라고 볼 수 있다.
3.4 저층 용존산소 영향인자
연안에서 용존산소는 성층과 기상 등 물리적인 요인과 광합성, 퇴적물 산소요구량 같은 생지화학적 요인의 영향으로 조석주기, 일주기 및 계절주기 등 다양한 시간 변동을 나타낸다(Kemp et al.[2009]; Nezlin et al.[2009]). 진해만은 폐쇄성 내만으로 외해수와의 해수교환이 원활하지 않아(Kim et al.[2016]) 매년 5월에서 9월 사이에 저층 빈산소가 형성되는데(Lim et al.[2006]; Lee et al.[2017]), 주로 일사량 증가로 형성되는 수온성층의 영향을 받는다(Lee et al.[2017]; Lim et al.[2018]). 퇴적물 산소요구량 또한 빈산소수괴 형성에 영향을 미친다. 수온이 증가하면 산소 용해도가 감소하고 유기물 분해를 통해 산소를 소비하는 박테리아 호흡이 증가하여 용존산소는 감소하게 된다(Shin et al.[2018]). 본 연구해역인 당동만은 외해와 해수교환이 원활하지 않은 반폐쇄성만으로 생지화학적 영향(수층, 퇴적물 산소요구량)보다 표층과 저층의 수온차와 빈산소수괴 발생과 가장 상관관계가 높은 것으로 나타났다(Kang et al.[2020], Lee et al.[2017]). 그러나 간헐적으로 집중호우시기에 형성된 염분성층이 수층의 안정성을 강화시켜 저층 빈산소가 지속된다(Kim et al.[2012]; Lee et al.[2018]). Kim et al.[2018]은 밀도성층을 수온성층과 염분성층으로 구분하여 시기에 따른 영향력을 파악하였다. 본 연구에서 저층 용존산소 변동에 영향을 미치는 성층의 영향을 파악하고자 수층별 수온과 염분을 연속적으로 관측하였지만 앞서 언급한 바와 같이 염분 자료의 신뢰성 문제로 본 연구에서는 염분 자료를 활용하지 못하였다. 향후 염분자료를 활용할 수 있도록 YSI 관측값을 활용한 염분 오차 보정을 수행하는 작업과 함께 데이터의 자료의 단절구간에 대한 보간 기법을 적용하여 입력자료로 활용할 수 있는 방안 마련이 필요 하다.
한편, 하천에서 용존산소를 예측하게 위한 모델을 개발하고자 했던 선행연구에서는 pH, 용존무기물질, 전기전도도가 중요한 변수로 선택되었다(Kim et al.[2021], Han et al.[2023]). 그러나 현재까지 연안에서는 이러한 변수들을 연속적으로 관측하기 어려워 저층 용존산소를 예측하는 변수로 활용하기에는 한계가 있다. 연안에서 물리적 요인뿐만 아니라 생지화학적 요인도 저층 용존산소 변동에 영향을 미칠 것으로 판단되므로 이를 활용할 수 있는 방안 모색이 향후 필요할 것으로 판단된다.
4. 결 론
본 연구에서는 연안해역에서 양식생물의 대량 폐사를 일으키는 빈산소수괴의 단기예측 가능성을 파악하고자 딥러닝 모델을 활용하여 저층 용존산소의 시간변동을 예측한 후 모델별로 예측 정확도를 비교하였다. 딥러닝 모델은 최근 시계열 예측에 많이 활용되고 있는 대표적인 순환신경망 모델인 LSTM과 GRU 모델과 합성곱 신경망인 1D-CNN 모델을 활용하였다. 모델의 예측 정확도에 영향을 미치는 최적의 입력변수와 매개변수를 선정한 후 딥러닝 모델에 적용하였으며, 각 예측선행시간(1~72 시간)을 고려하여 저층 용존산소의 시간변동을 예측하였다. 각 모델의 평가지표를 비교한 결과, LSTM 모델은 CC 0.62~0.97, R2 0.38~0.94, MSE 0.19~2.15 mg/L, RMSE 0.44~1.47 mg/L, MAE 0.29~1.20 mg/L로 예측 성능이 가장 낮은 것으로 나타났으며, 1D-CNN 모델은 CC 0.70~0.97, R2 0.45~0.95, MSE 0.19~1.90 mg/L, RMSE 0.43~1.38 mg/L, MAE는 0.28~1.06 mg/L로 예측 성능이 가장 우수한 것으로 나타냈다. GRU 모델과 1D-CNN 모델은 예측 시간이 증가할수록 예측성능 뿐만 아니라 LSTM 모델보다 저층 용존산소의 단주기 변동성을 더 잘 모의하였으며, 이는 각 모델 간의 구조 차이에 기인한 결과로 파악되었다. 따라서 예측 정확도 확보와 단주기 변동 재현성이 반영된 모델을 구축하기 위해서는 LSTM 모델보다 GRU나 1D-CNN 모델이 더 적합한 것으로 판단된다. 본 연구에서는 성층인자로 △T(표층 수온과 저층 수온차)을 활용하였으며, 기존 연구에 따르면 연구 지역에서 강우시기에 △S(표층 염분과 저층 염분차) 또한 영향을 미치는 것으로 나타났다. 이는 시기에 따라 저층 용존산소에 영향을 주는 성층 영향이 다를 수 있음을 시사한다. 따라서 앞서 언급한 것처럼 염분자료의 신뢰성 확보를 통해 복합적인 성층 자료를 수집하고, 이를 바탕으로 분석과 해석이 필요할 것으로 판단된다.
빈산수소괴로 인한 수산피해를 최소화하기 위해서는 양식현장에서 어민들이 충분한 시간을 두고 사전 대비할 수 있도록 빈산소수괴 발생 예측정보 제공이 필요하다. 본 연구에서 제시한 딥러닝 모델의 예측 성능은 예측선행시간 48시간 이전까지 저층 용존산소의 시간변동을 안정적으로 예측할 수 있다는 것을 확인할 수 있었다. 딥러닝을 활용한 빈산소수괴 발생 예측 연구는 아직까지 초기단계로 향후 관측자료의 추가적인 확보, 모델의 매개변수 최적화 등을 수행하여 예측 정확도를 향상시킨다면 빈산소수괴로 인한 수산피해 저감에 기여할 수 있을 것으로 판단된다.
Acknowledgments
본 논문은 2024년도 국립수산과학원 수산과학연구사업(R2024044)의 지원으로 수행되었습니다.
References
-
Ahmed A.M., 2017, Prediction of dissolved oxygen in Surma River by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (ANNs), J. King Saud Univ- Eng Sci, 29(2), 151-158.
[https://doi.org/10.1016/j.jksues.2014.05.001]

-
Azizjon, M., Jumabek, A. and Kim, W., 2020, February. 1D CNN based network intrusion detection with normalization on imbalanced data. In 2020 international conference on artificial intelligence in information and communication (ICAIIC), IEEE, pp. 218-224.
[https://doi.org/10.1109/ICAIIC48513.2020.9064976]

-
Breitburg, D., Levin, L.A., Oschlies, A., Grégoire, M., Chavez, F.P., Conley, D.J., Garçon, V., Gilbert, D., Gutiérrez, D., Isensee, K., Jacinto, G.S., Limburg, K.E., Montes, I., Naqvi, S.W.A., Pitcher, G.C., Rabalais, N.N., Roman, M.R., Rose, K.A., Seibel, B.A., Telszewski, M., Yasuhara, M. and Zhang, J., 2018, Declining oxygen in the global ocean and coastal waters. Science 359(6371).
[https://doi.org/10.1126/science.aam7240]

-
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H. and Bengio, Y. (2014), Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078, .
[https://doi.org/10.3115/v1/D14-1179]

- Chung, J., Gulcehre, C., Cho, K. and Bengio, Y., 2014, Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555, .
-
Diaz, R.J., 2001, Overview of hypoxia around the world. J. Environ. Qual 30, 275–281. https://doi.org/10.2134/jeq2001.302275x.
[https://doi.org/10.2134/jeq2001.302275x]

-
Diaz, R.J. and Rosenberg, R., 2008, Spreading dead zones and con-sequences for marine ecosystems, Science 321, 926-929.
[https://doi.org/10.1126/science.1156401]

-
Han, M.S., Park, S.E., Choi, Y.J., Kim, Y.M. and Hwang, J.D., 2020, Prediction of Dissolved Oxygen in Jindong Bay Using Time Series Analysis, Korean Soc. Mar. Environ. Saf, 26(4), 382-391.
[https://doi.org/10.7837/kosomes.2020.26.4.382]

-
Hochreiter, S., Schmidhuber, J., 1997, Long short-term memory. Neural computation, 9(8), 1735-1780.
[https://doi.org/10.1162/neco.1997.9.8.1735]

-
Huan, J., Li, H., Li, M. and Chen, B., 2020, Prediction of dissolved oxygen in aquaculture based on gradient boosting decision tree and long short-term memory network: A study of Chang Zhou fishery demonstration base, China. Computers and Electronics in Agriculture, 175, 105530.
[https://doi.org/10.1016/j.compag.2020.105530]

-
Iskandaryan, D., Ramos, F. and Trilles, S. (2022), Bidirectional convolutional LSTM for the prediction of nitrogen dioxide in the city of Madrid. PloS one, 17(6).
[https://doi.org/10.1371/journal.pone.0269295]

-
Ji, X., Shang, X., Dahlgren, R.A. and Zhang, M., 2017, Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of Wen-Rui Tang river, China, Environ. Sci. Pollut. Res, 24(19), 16062-16076.
[https://doi.org/10.1007/s11356-017-9243-7]

-
Kang, H., Kwon, M.S., You, S.J. and Kim, J.G., 2020, Keeling, R.F., The Prediction of Hypoxia Occurrence in Dangdong Bay, 26(1), Korean Soc. Mar. Environ. Saf pp. 65-74.
[https://doi.org/10.7837/kosomes.2020.26.1.065]

-
Keeling, R.F., Körtzinger, A. and Gruber, N., 2010, Ocean deoxygenation in a warming world. Annu. Rev. Mar. Sci 2, 199-229.
[https://doi.org/10.1146/annurev.marine.010908.163855]

-
Kemp, W.M., Testa, J.M., Conley, D.J., Gilbert, D. and Hagy, J.D., 2009, Temporal responses of coastal hypoxia to nutrient loading and physical controls, Biogeosciences 6, 2985-3008.
[https://doi.org/10.5194/bg-6-2985-2009]

-
Kim, M.J., Byeon, S.J., Kim, K.M. and Ahn, J.H., 2021, Selection of Input Factors and Comparison of Machine Learning Models for Prediction of Dissolved Oxygen in Gyeongan Stream, J. Korean Soc. Environ. Eng, 43(3), 206-217.
[https://doi.org/10.4491/KSEE.2021.43.3.206]

-
Kim, S.Y., Lee, Y.H., Kim, Y.S., Shim, J.H., Ye, M.J. and Jeon, J.W., 2012, Characteristics of marine environmental in the hypoxic season at Jinhae Bay in 2010. Korea J. Nat. Conserv 6, 115-129.
[https://doi.org/10.11624/KJNC.2012.6.2.115]

-
Kim, S.Y., Hayami, Y., Tai, A. and Tada, A., 2018, The mechanism of bottom water DO variation in summer at the northern mouth of Isahaya Bay, Japan. J. Oceanogr. 74, 595-605.
[https://doi.org/10.1007/s10872-018-0467-z]

-
Lee, J.Y, Kim, S. G. and An, S., 2017, Dynamics of the physical and biogeochemical processes during hypoxia in Jinhae Bay, South Korea. J. Coast. Res., 33(4), 854-863.
[https://doi.org/10.2112/JCOASTRES-D-16-00122.1]

-
Lee, J.Y, Park, K.T, Lim, J.H., Yoon, J.E. and Kim I.N., 2018, Hypoxia in Korean coastal waters: a case study of the natural Jinhae Bay and artificial Shihwa Bay. Frontiers in Marine Science 5, 70.
[https://doi.org/10.3389/fmars.2018.00070]

-
Li, W., Wu, H., Zhu, N., Jiang, Y., Tan, J. and Guo, Y., 2021, Prediction of dissolved oxygen in a fishery pond based on gated recurrent unit (GRU). Information Processing in Agriculture, 8(1), 185-193.
[https://doi.org/10.1016/j.inpa.2020.02.002]

-
Lim, H.S., Diaz, R.J., Hong, J. and Schaffner, L.C., 2006, Hypoxia and benthic community recovery in Korean coastal waters, Mar. Pollut. Bull. 52, 1517-1526.
[https://doi.org/10.1016/j.marpolbul.2006.05.013]

-
Lim, J.H., Lee, S.H., Park, J., Lee, J., Yoon, J.E. and Kim, I. N., 2018, Coastal Hypoxia in the Jinhae Bay, South Korea: Mechanism, Spatiotemporal Variation, and Implications (based on 2011 survey), J. Coast. Res. 85, 1481-1485.
[https://doi.org/10.2112/SI85-297.1]

-
Lim, H., An, H., Choi, E. and Kim, Y., 2020, Prediction of the DO concentration using the machine learning algorithm: case study in Oncheoncheon, Republic of Korea, Korean Journal of Agricultural Science, 47, 1029-1037.
[https://doi.org/10.5194/egusphere-egu2020-6690]

-
Moriasi, D.N., Gitau, M.W., Pai, N. and Daggupati, P., 2015, Hydrologic and water quality models: Performance measures and evaluation criteria. Transactions of the ASABE, 58(6), 1763-1785.
[https://doi.org/10.13031/trans.58.10715]

-
Nezlin, N.P., Kamer, K., Hyde, J. and Stein, E.D. 2009, Dissolved oxygen dynamics in a eutrophic estuary, Upper Newport Bay, California. Estuar Coast Shelf Sci 82, 139-151.
[https://doi.org/10.1016/j.ecss.2009.01.004]

- Qin, H., 2019, Comparison of deep learning models on time series forecasting: A case study of dissolved oxygen prediction. arXiv preprint arXiv:1911.08414, .
- Pamatmat, M.M. 1980, Faculaive anaerobiosis of benthos. In, marine benthic dymanics, edited by K.R. Tenore and B.C. Coull, University of South Carolina, Columbia. pp. 69-90.
-
Park, S.S. and Kim, K.H., 2021, Prediction of DO Concentration in Nakdong River Estuary through Case Study Based on Long Short Term Memory Model, Journal of Korean Society of Coastal and Ocean Engineers, 33(6), 1-8.
[https://doi.org/10.9765/KSCOE.2021.33.6.238]

-
Park, S.S., Kim, B.K. and Kim, K.H., 2022, Prediction in Dissolved Oxygen Concentration and Occurrence of Hypoxia Water Mass in Jinhae Bay Based on Machine Learning Model, Journal of Korean Society of Coastal and Ocean Engineers, 34(3), 47-57.
[https://doi.org/10.9765/KSCOE.2022.34.3.47]

-
Shin, H.H., Li, Z., Lim, D., Lee, K.W., Seo, M.H. and Lim, W.A., 2018, Seasonal production of dinoflagellate cysts in relation to environmental characteristics in Jinhae-Masan Bay, Korea: One-year sediment trap observation. Estuarine, Coastal and Shelf Science 215, 83-93.
[https://doi.org/10.1016/j.ecss.2018.09.031]

- Shin, U.H., Kim, D.K. and Park, K.S., 2021, A Study on the Selection of AI Prediction Models According to the Characteristics of Time Series, in proc. of KIIS Spring Conference, Seoul, Korea, 173-174.
-
Zhang, Y., Fitch, P., Vilas, M.P. and Thorburn, P.J., 2019, Applying multi-layer artificial neural network and mutual information to the prediction of trends in dissolved oxygen. Frontiers in Environmental Science, 7(46).
[https://doi.org/10.3389/fenvs.2019.00046]