인공지능 모델을 활용한 실시간 수질평가지수 예측
초록
현재 해양수산부에서 연안 오염우심해역의 해양환경을 상시 측정하기 위해 해양수질자동측정망 자료를 제공하고 있다. 아울러 우리나라는 해양환경을 직관적으로 평가하기 위하여 수질평가지수(water quality index, WQI)를 사용하고 있다. 하지만, 해양환경측정망 자료는 WQI를 제공하고 있으나 해양수질자동측정망 자료는 WQI를 계산하기 위한 수질 자료가 충분하지 않다. 이 연구는 실시간으로 수질 변화를 평가하기 위해서 해양환경측정망 자료를 학습한 인공지능(artificial intelligence, AI) 모델(model)을 이용하여 보정(calibration)된 수질자동측정망 자료의 WQI를 예측하고자 한다. 특별관리해역의 수질자동측정망 자료 중 결측치(missing value)가 비교적 적은 부산수영, 광양적량, 마산삼귀, 인천송도, 시화조력, 시화반월 측정소 자료를 활용하였다. 보정을 위해 수질자동측정소와 가장 인접한 해역별 정점의 해양환경즉정망자료를 활용하였다. Cook의 거리(Cook’s distance) 비교로 이상치를 제거하고 선형회귀(linear regression)를 통해 해양환경측정망과 동일한 조사 시간의 수질자동측정망 자료 중 결정계수(coefficient of determination)값이 큰 변수의 자료만을 보정하였다. 해양환경측정망 자료를 훈련자료(training datasets)로 사용하고 보정된 수질자동측정망 자료를 검증 자료(test datasets)를 사용하여 다양한 알고리즘(algorithm)(MLR, SVR, XGBR, ETR, ANN, ELM, NFN, ANFIS, GANN)으로 학습한 모델의 예측 성능을 평균제곱근오차(root mean square error, RMSE), 평균절대오차(mean absolute error, MAE)로 평가하였다. 평가 결과 각 해역별로 최적 알고리즘과 예측성능은 상이하였고 수질이 나쁜 경우(WQI가 클수록) 예측성능이 나쁘고 일관성이 부족하였다. 자료와 보정의 품질을 향상시킨다면 실시간으로 수질자동측정망 자료의 WQI를 정확히 예측하여 수질오염 경보와 지속가능한 해양환경관리가 가능할 것이다.
Abstract
The Ministry of Oceans and Fisheries is providing real-time data from the Real-time Water Quality Monitoring System(RWQMS) to monitor the marine environment in areas of concern for pollution. The Korean government uses the Water Quality Index(WQI) to evaluate the state of the marine environment, but the data from the RWQMS is insufficient to calculate the WQI. This study aims to predict the WQI by using an Artificial Intelligence(AI) model trained on data from the Marine Environment Monitoring System(MEMS) to track changes in water quality in real-time. The study focuses on data from six specific RWQMS stations(Busan Suyeong, Gwangyang Jeongyang, Masan Samgwi, Incheon Songdo, Sihwa TPP, and Sihwa Banweol) with relatively low levels of missing data. The data from nearby MEMS stations was used for calibration. Outliers were removed and the RWQMS data was calibrated through linear regression, considering only data with high coefficients of determination(R2). The predictive performance of the model, trained using various algorithms(MLR, SVR, XGBR, ETR, ANN, ELM, NFN, ANFIS, and GANN), was evaluated using Root Mean Square Error(RMSE) and Mean Absolute Error(MAE). The results showed that the optimal algorithm and predictive performance varied by location and poor water quality resulted in poor predictive performance and consistency. Better data quality and calibration improve real-time WQI predictions in the RWQMS, enabling early warnings for water pollution and promoting sustainable management of the marine environment.
Keywords:
Real-time water quality monitoring system, Water quality index, Marine environment monitoring system, Artificial intelligence키워드:
해양수질자동측정망, 수질평가지수, 해양환경측정망, 인공지능1. 서 론
지속적인 해양 개발·이용행위가 증가하면서 해양의 오염부하가 가중되고 있다. 해양오염은 해양건강성을 위협하고 해양생태계를 훼손시킬 수 있다. 해양을 지속가능하게 보전·관리하기 위하여 우리나라는 해양환경정보를 제공하고 있다. 이중 연안 오염우심지역의 해양환경 상태를 상시적으로 감시하는 해양수질자동측정망(real-time water quality monitoring system, RWQMS)을 2005년부터 운영하고 있다. 해양수질자동측정망 자료는 연안오염총량관리 수립·시행, 육상기인오염원 및 기후변화 감시 등에 활용되고 있다. 해양수질자동측정망의 조사 정점은 인천시화 3기(시화조력, 시화반월, 인천송도), 마산 3기(마산삼귀, 마산봉암, 마산양덕), 광양 3기(광양망덕, 광양초남, 광양적량), 부산(부산수영), 새만금, 울산(울산온산), 한강하구(인천강화), 낙동강하구 2기(낙동을숙, 낙동명지), 영산강하구 2기(영산영암, 영산목포), 금강하구, 천수만이 있다. 수질·기상측정센서는 수온(temperature), 염분(salinity), 수소이온농도(pH), 전기전도도(electrical conductivity, EC), 용존산소(DO), 탁도(turbidity), 엽록소 a(Chlorophyll a, Chl-a), 남조류(blue-green algae, BGA)를 5초 간격으로 측정하여 측정망에 5분 평균한 값을 제공한다. 수질측정장치는 화학적산소요구량(chemical oxygen demand, COD), 총 질소(total nitrogen, TN), 총인(total phosphorus, TP), 암모니아성질소(NH3-N), 질산성질소+아질산성질소(NO3-N+NO2-N), 규산규소(SiO2-Si)를 1시간 간격으로 측정하여 측정망에서 제공한다. 확정자료에서는 기상자료(일사량, 기온, 상대습도, 풍속, 풍향, 강수량)와 인산염인(PO4-P) 자료를 추가로 제공한다. 해양환경측정망(marine environment monitoring system, MEMS)은 연안 및 근해역의 해양환경 상태를 평가하기 위해 연 4회(2, 5, 8, 11월) 수심, 표층과 저층의 수온, 염분, pH, DO, COD, NH3-H, NO2-N, NO3-N, 용존무기질소(dissolved inorganic nitrogen, DIN), TN, 용존무기인(dissolved inorganic phosphorus, DIP), TP, SiO2-Si, 부유물질(suspended solids, SS), Chl-a와 투명도(Secchi disk depth, SD), 수질평가지수(water quality index, WQI) 등급 자료를 제공하고 있다.
우리나라는 해양수산부고시 제2018-10호「해양환경기준」의 생태기반 해수수질 기준을 바탕으로 WQI를 계산하여 수질을 평가하고 있다. 생태구별 기준값에 대하여 5개 수질 항목(투명도, 저층 DO, 표층 DIN, DIP, Chl-a)의 점수를 대입하여 WQI를 산정한다. WQI를 통해 부영양화의 인과관계를 종합적으로 고려하여 직관적인 해양환경 평가를 할 수 있다. 하지만 해양수질자동측정망에서는 이중 표층 Chl-a 이외의 자료는 제공하지 않아 WQI를 계산할 수 없다. Jeon et al.[2020]은 광양만의 해양수질자동측정망(광양적량) 수질 자료와 해양환경측정망 WQI 등급 자료를 결합한 자료를 활용하여 학습한 기계학습(machine learning, ML) 및 인공신경망(artificial neural network, ANN) 기반 모델로 해양수질자동측정망자료의 WQI 등급을 예측했다. 하지만 해양환경측정망과 해양수질자동측정망 자료는 조사일자가 동일하더라도 채수 위치, 조사 시간, 시험조건 및 방법이 상이하여 오분류(misclassification)된 WQI 등급으로 모델이 훈련(train)하는 문제가 있을 수 있다.
이 연구에서는 해양환경측정망 자료를 바탕으로 보정(calibration)을 하고 이상치(outlier)를 제거한 해양수질자동측정망 자료의 WQI를 예측하고자 한다. Kulisz et al.[2021]은 ANN 모델의 입력변수(input variable)를 선택하기 위해 지하수 수질자료를 이용하여 다중선형회귀(multiple linear regression, MLR) 모델을 통해 WQI를 예측하고 개별 예측값에 대해 Cook의 거리(Cook’s distance)를 계산하여 이상치를 제거했다. 해양환경측정망 자료를 훈련한 모델로 보정된 해양수질자동측정망 자료의 WQI를 예측하였을 때 오염우심지역의 수질을 실시간으로 보다 정확하게 평가할 수 있을 것이다. Park et al.[2013]은 실시간 해양환경 분석 및 예측 시스템 모델을 개발하기 위하여 통영지역의 10년 적조자료를 서포트 벡터 머신(support vector machine, SVM), 역전사신경망(back propagation neural network, BPNN), 나이브 베이즈 분류기(Naive Bayes classifier, NBC) 모델로 예측한 결과 NBC에서 가장 높은 예측 정확도를 보였다. Lee et al.[2018]은 이네비게이션(e-Navigation) 선박에서 실시간으로 수집된 해양환경 빅데이터(big data)를 효율적으로 처리·해석할 수 있는 방안으로 앙상블(ensemble) 기법과 딥 러닝(deep learning) 기법을 제안했다. Kim et al.[2022]은 해양환경측정망 자료를 학습한 ML 기반 모델을 이용하여 시화호의 WQI 등급을 예측하였고 모델의 입력변수를 축소하여도 높은 정확도로 예측했다.
또한 WQI 등급 보다는 WQI를 예측한다면 보다 정밀하게 수질상태를 실시간으로 진단할 수 있다. Gazzaz et al.[2012]은 quick propagation(QP) 훈련 알고리즘 기반 ANN 모델로 강의 10년 수질자료를 학습하여 WQI를 예측하고 평가한 결과 최적 뉴런(neuron)의 수, 학습률(learning rate), QP 계수를 도출했다. Hameed et al.[2017]은 방사형 기저 함수 신경망(radial basis function neural network, RBFNN)과 BPNN 모델로 강의 10년 수질자료를 학습하여 WQI를 예측한 결과 RBFNN의 예측 정확도가 더 높았다. Yaseen et al.[2018]은 12년 강의 수질자료를 다양한 최적화(optimization) 방법과 결합한 적응형 신경 퍼지 추론 시스템(adaptive neuro fuzzy inference system, ANFIS) 모델로 학습하여 WQI를 예측한 결과 매우 좋은 성능을 보였다. Li et al.[2019]은 반딧불 알고리즘(firefly algorithm, FFA)으로 최적화된 서포트 벡터 회귀(support vector regression, SVR) 모델로 강의 10년 수질자료를 학습한 결과 단일 SVR 모델보다 더 좋은 성능을 보였다. Bui et al.[2020]은 저수지의 6년 수질자료를 M5P, 랜덤 포레스트(random forest, RF), 랜덤 트리(random tree, RT), reduced error pruning tree(REPT)와 배깅(bagging, BA), cross-validation parameter selection(CVPS), randomizable filtered classifier(RFC) 최적화 방식을 혼합(hybrid)한 알고리즘 기반 모델로 학습한 결과 BA-RT 모델의 WQI 예측성능이 가장 우수하였다. Abba et al.[2020]은 extreme gradient boosting(XGBoost), 유전 프로그래밍(genetic programming, GP), 선형회귀(linear regression, LR), 단계적 선형회귀(step wise linear regression, SWLR), 극학습기계(extra learning machine, ELM) 알고리즘 기반 모델로 강의 12년 수질자료를 학습하여 WQI를 예측한 결과 GP 변수선택 기반 ELM 모델의 예측 정확도가 가장 높았다. Asadollah et al.[2021]은 강의 20년 수질자료를 학습한 앙상블 ML 알고리즘인 extra tree regression(ETR) 모델의 WQI 예측성능을 SVR, 결정트리회귀(decision tree regression, DTR) 모델과 비교한 결과 ETR > SVR > DTR 순의 예측 정확도를 보였다. Kouadri et al.[2021]은 민감도 분석(sensitivity analysis)를 통해 선택된 변수의 수질자료만을 학습한 MLR, RF, M5P, 랜덤 서브 스페이스(random subspace, RSS), 추가 회귀(additive regression, AR), ANN, 서포트 벡터 회귀(support vector regression, SVR), 국소가중선형회귀(locally weighted linear regression, LWLR) 모델로 지하수의 WQI를 예측한 결과 RF 모델이 가장 우수한 예측성능을 보였다. Abba et al.[2022]은 유전 알고리즘-인공신경망(genetic algorithm-emotional artificial neural network, GA-EANN) 모델을 BPNN, MLR 모델과 WQI 예측성능을 비교하였을 때 더 적은 입력변수로 WQI를 정확하게 예측했다. Khozani et al.[2022]은 다층퍼셉트론(multi-layer perceptron, MLP), 장단기메모리(long short term memory, LSTM), 합성곱 신경망(convolutional neural network, CNN) 모델로 강의 10년 수질자료를 학습하여 WQI를 예측한 결과 LSTM 모델의 예측 정확도가 가장 높았다. Khan et al.[2022]은 1년 동안 측정한 호수의 수질자료를 LR, gradient boosting regression(GBR), RF, SVR 모델로 학습하여 WQI를 예측한 결과 SVR 모델이 가장 좋은 성능을 보였다.
이 연구에서는 「해양환경관리법」 제15조 1항에 따라 지정된 특별관리해역 중 부산연안, 광양만, 마산만, 시화호, 인천연안의 WQI를 각 해역의 해양수질자동측정망 자료로 예측하고자 한다. 향후 인공지능 모델의 연속 관측자료 학습으로 WQI를 예측하여 실시간 생태기반 해양환경 평가·감시가 가능할 것이라 판단된다.
2. 연구 방법
2.1 대상 지역
연구 지역은 「해양환경관리법」 제15조 1항에 따라 지정된 특별관리해역 중 5개 해역(부산연안, 광양만, 마산만, 시화호, 인천연안)이다. 여기서 특별관리해역은 해양환경기준 유지가 어려운 해역 또는 해양환경 및 생태계의 보전에 현저한 장애가 있거나 장애를 초래할 우려가 있는 해역을 의미한다. 생태구(ecological region) 별로는 부산연안, 광양만, 마산만은 대한해협(Korea Strait) 생태구, 시화호, 인천연안은 서해중부(Central West) 생태구로 분류된다. 특히, 특별관리해역 내 오염이 심각한 지역은 집중적인 해양환경관리를 위해 해양수질자동측정소를 운영하고 있다. 이 연구에서는 특별관리해역 중 5년 이상 해양수질자동측정망 자료를 확보할 수 있는 오염우심지역(부산수영, 광양적량, 마산삼귀, 시화조력, 시화반월, 인천송도)의 실시간 WQI를 예측하고자 한다. 울산연안도 특별관리해역에 해당하나 해양수질자동측정망(울산온산)이 운영되지 않은 시기가 많고 수질자동측정장치에서 해양 수질평가에 중요한 지표인 COD, TN, TP, NH3-N은 측정하고 있지 않아 대상지역에서 제외했다. 해양수질자동측정망 미운영 시기가 많거나 측정항목이 적은 측정소(광양망덕, 광양초남, 마산봉암, 마산양덕, 인천강화)도 제외했다. 보정에 필요한 자료를 확보하기 위해 해양수질자동측정소를 기준으로 직선거리가 가장 가까운 해양환경측정망 정점을 선정했다. Table 1은 이 연구의 대상지역인 해양수질자동측정망 정점과 해양환경측정망 정점에 대한 경위도 좌표 정보이다.
2.2 모델 학습 자료
해양환경측정망 자료(부산연안, 광양만, 마산만, 시화호, 인천연안)를 해양수산부 해양환경정보포털에서 수집했다. 해역별 해양환경측정망 자료의 정보는 Table 2와 같다. 해역별 해양환경측정망 자료 중 표층 수온(Temp_Sur), 수소이온농도(pH_Sur), 용존산소(DO_Sur), 부유물질(SS_Sur), 염분(Salinity_Sur), 화학적산소요구량(COD_Sur), 엽록소 a(Chl-a_Sur), 암모니아성질소(NH3-N_Sur), 질산성질소(NO3-N_Sur), 총질소(TN_Sur), 용존무기인(DIP_Sur), 총인(TP_Sur), WQI 자료를 훈련용 자료(training dataset)로 사용했다. 2021년 8월까지 확정된 해양수질자동측정망(부산수영, 광양적량, 마산삼귀, 시화반월, 시화조력, 인천송도) 자료도 해양환경정보포털에서 수집했다. 측정소 별로 미운영 시기가 있었으나 5년 이상의 자료(부산수영 : 2013-2016, 2018-2021; 광양적량 : 2014, 2017-2021; 마산삼귀 : 2014-2021; 시화반월 : 2013-2015, 2017-2021; 시화조력 : 2013-2021; 인천송도 : 2017-2021)를 확보하였다. 해역별 해양환경측정망과 동일한 조사 일시의 해양수질자동측정망 자료 중 표층 수온(Temp_Sur), 수소이온농도(pH_Sur), 용존산소(DO_Sur), 탁도(Turbidity_Sur), 염분(Salinity_Sur), 화학적산소요구량(COD_Sur), 엽록소 a(Chl-a_Sur), 암모니아성질소(NH3-N_Sur), 질산성질소(NO3-N_Sur), 총질소(TN_Sur), 인산염인(PO4-P_Sur), 총인(TP_Sur) 자료를 추출했다. 해역별 해양수질자동측정망 정점과 가장 인접한 해양환경측정망 정점의 자료를 추출하여 동일 조사일시에 측정된 해양수질자동측정망 자료와 결합했다. 결합한 자료에서 수질항목 별로 결측치(missing value)를 제거했다.
개별 수질항목에 대해 해양수질자동측정망 자료를 설명변수(x, explanatory variable), 해양환경측정망 자료를 반응변수(y, response variable)로 설정하여 단순선형회귀분석(simple linear regression)을 수행했다. 여기서 해양수질자동측정망 자료 중 탁도(Turbidity_Sur), 인산염인(PO4-P)은 각각 해양환경측정망 자료 중 연관성이 있는 부유물질(SS_Sur), 용존무기인(DIP_Sur)에 대응시켰다. 회귀분석 결과를 통해 Eq. 1과 같이 레버리지(h, leverage)값을 계산할 수 있다. 레버리지는 특정 설명변수 값이 다른 설명변수 값과 얼마나 떨어져 있는지 나타내는 척도이다. 여기서 i는 관측(observation) 번호(index), n은 관측의 수, H는 투영행렬(projection matrix), x는 설명 변수 값, X는 [관측치×설명변수] 크기의 설계행렬(design matrix), T는 전치행렬(transposed matrix)을 의미하며 결론적으로 hii는 투영 행렬 H의 i번째 대각 원소(diagonal element)로 i번째 관측의 레버리지 값을 의미한다.
| (1) |
이를 i번째 설명변수 값(xi)과 설명변수 값들의 평균 간 가중 거리(weighted distance)로 나타내면 i번째 반응변수 값(yi)이 i번째 예측값(predicted value, )에 미치는 영향을 Eq. 2와 같이 표현될 수 있다.
| (2) |
오차(ε, error)는 모집단(population)의 회귀분석 결과 실제값(true value)과 예측값의 차이로 정의하고 잔차(residual, )는 표본집단(sample)의 회귀분석 결과 실제값과 예측값의 차이로 설명된다. 잔차의 분산(variance)을 레버리지로 표현을 하면 Eq. 3과 같다. 여기서 은 i번째 잔차의 분산, σ2는 오차의 분산을 의미한다.
| (3) |
오차의 분산은 입력변수 값에 따라서 같을 수 있지만 잔차의 분산은 모든 입력변수 값에서 다르다. 그러므로 잔차를 오차의 표준편차 추정값()과 레버리지로 나누어 표준화한 잔차(Studentized residual, ti)는 Eq. 4와 같다.
| (4) |
이 연구에서는 이상치(outlier)를 제거하기 위하여 Fox의 이상치 추천법(Fox’s outlier recommendation)에 따라 Cook의 거리를 비교했다. Cook의 거리는 잔차와 레버리지 값이 큰 특정 관측치가 선형회귀모델 계수(parameter)의 최소자승(least square) 결정에 미치는 영향력(influence)을 평가하는 값이다(Cook[1977]). 특정 관측에 대해 잔차와 레버리지 값이 클수록 Cook의 거리가 커지고 이상치에 가깝다. Cook의 거리는 Eq. 5를 통해서 계산할 수 있다. 여기서 는 i번째 관측을 제거할 때 예측값, s2은 회귀모델의 평균제곱오차(mean squared error, MSE)를 의미한다. p는 개별 관측치에 대한 예측변수(predictor)의 수이다.
| (5) |
마지막으로 Cook의 거리(Di)는 Eq. 6과 같이 레버리지와 표준화된 잔차로 표현할 수 있다.
| (6) |
Cook의 거리 한도(cutoff)는 통상적으로 4/n을 사용하고 있다. 이 연구에서도 개별 관측치에 대해 Cook의 거리를 계산하여 4/n 이상인 경우 이상치로 간주했다. 개별 입력변수의 선형회귀모델에서 더 이상 이상치가 발생하지 않을 때까지 이상치 제거 작업을 반복했다. 이상치 제거 단계 마다 수질항목 별 결정계수(coefficient of determination, R2)를 비교하여 결정계수가 가장 큰 선형회귀식을 이용하여 해양수질자동측정망 자료를 보정했다. 해양수질자동측정망 자료가 해양환경측정망 자료에 대한 설명력이 충분하지 않은(결정계수가 작은) 변수는 학습에서 제외하였다. 보정한 해양수질자동측정망 자료와 동일한 조사시기의 해양환경측정망 자료 중 WQI 자료를 결합하여 평가용 자료(testing dataset)로 사용했다.
2.3 모델 알고리즘
WQI 예측 모델의 알고리즘은 기존 문헌에서 보고된 모델 중 가장 WQI 예측 결과가 우수한 모델의 알고리즘을 선택했다(Gazzaz et al.[2012]; Yaseen et al.[2018]; Abba et al.[2020]; Asadollah et al.[2021]; Kulisz et al.[2021]; Abba et al.[2022]; Khan et al.[2022]).
다중선형회귀(multiple linear regression, MLR)는 예측변수가 복수인 선형회귀이다. 다중선형회귀식은 Eq. 7과 나타낼 수 있다. 여기서 i는 관측 번호, p는 예측변수의 수, n은 관측의 수이다. Xip는 p번째 독립변수(independent variable)의 i번째 관측치를 의미한다. βp는 다중선형회귀를 통해 얻어지는 p번째 독립변수의 계수, εi은 i번째 관측의 동분산 표준오차(identically distributed normal error)를 의미한다. 결론적으로 Yi는 i번째 관측의 다중선형회귀 모델 예측값을 의미한다.
| (7) |
SVR은 Eq. 8과 같이 손실함수(loss function, LSVR)를 회귀에 도입하여 실제값과 예측값의 차이(deviation)를 작게 하면서 평평한(flat) 함수를 찾는 것이 목표이다(Smola and Scholkopf[2004]). 여기서 ε은 실제값과 예측값의 차이에 대한 제한 범위(margin)를 의미한다. n은 관측의 수, xi는 i번째 관측의 독립변수(independent variable), yi는 i번째 관측의 종속변수(dependent variable), w, b는 회귀 계수, ξ은 여유변수(slack variable)로 제약 조건(constraint)을 완화하여 차이를 허용하도록 설정한 변수이다. ξi은 i번째 관측에 대해 상한선으로부터 양(+)의 거리, 은 음(-)의 거리를 의미한다. C는 함수의 제한된 최적화(optimization) 문제에서 일정 비율 패널티(penalty)를 부여하는 상수(constant)이다.
| (8) |
손실함수의 해(solution)를 계산하기 쉽도록 Lagrangian dual problem으로 손실함수를 재구성한다. 그리고 Karush-Kuhn-Tucker(KKT) 조건에 따라 미지수에 대한 목적함수의 미분값이 0일 때 최적해를 가지므로 손실함수를 미분(derivative)하여 회귀 계수(w, b)를 구할 수 있다. 하지만 비선형성(nonlinearity)을 가지는 회귀식에 적용하려면 저차원(i.e. input space)의 자료를 내적(dot product)하여 고차원(i.e. feature space)으로 변환해주는 매핑(mapping)이 필요하다. 방사형 기저 함수(radial basis function, RBF), 선형(linear), 다항식(polynomial), 시그모이드(sigmoid) 함수와 같은 커널함수(kernel function)를 손실함수에 추가하여 간단히 고차원 공간으로 매핑할 수 있다. 최종적으로 Eq. 9와 같이 비선형적인 회귀식을 도출할 수 있다. 여기서 αi는 i번째 관측의 Lagrangian multiplier, k(xi, xi)는 i번째 관측의 커널함수를 의미한다.
| (9) |
Gradient boosting은 DT 기반의 앙상블(ensemble) 기계학습 알고리즘이다. 그 중 extreme gradient boosting (XGBoost)은 가장 좋은 성능을 나타내는 알고리즘으로 알려져있다. 의사결정나무 앙상블 모델은 Eq. 10과 같이 나타낼 수 있다. 여기서 D는 자료(dataset), n은 사례(example), m은 특성(feature)을 의미한다. Eq. 11-12에서는 는 예측 출력값(predicted output), K는 나무의 수, fk는 k번째 나무, F는 회귀 나무의 공간(space), q는 개별 나무의 구조(structure), T는 잎(leaf)의 수, w는 잎의 가중치(weight)이다. 개별 잎의 가중치를 모두 합하여 최종 예측을 할 수 있다.
| (10) |
| (11) |
| (12) |
학습의 최적화를 위해서 손실 및 정규화(regularized) 목적함수(objective function)를 최소화하여야 한다. Eq. 13은 정규화 함수이다. 여기서 l은 미분가능한 볼록(convex) 손실함수, Ω(Eq. 14)는 과적합(overfitting)을 피하기 위해 모델의 복잡함(complexity)에 대해 패널티를 부여하는 항(term)을 의미한다.
| (13) |
| (14) |
Gradient boosting에서는 Eq. 15와 같이 t번째 반복 단계(iteration step)에서 i번째 사례에 대한 예측값을 이라고 하면 모델이 계속 학습하면서 t번째 새로운 함수 ft를 추가하여 목적함수를 최소화하여야 한다.
| (15) |
가능한 모든 나무 구조에 대해 최적화를 하는 것은 시간이 오래 걸리므로 최적의 선택(locally optimal selection)을 하여 최종 해(globally optimal solution)를 구하는 탐욕 알고리즘(greedy algorithm)을 통해 단일 잎에 반복적으로 가지(branch)를 더하는 방식으로 신속한 최적화를 한다(Chen and Guestrin[2016]). Eq. 16은 나무의 분리(split) 후 손실 감소(loss reduction)를 의미하며 분리 대상(split candidate)을 찾기 위해 사용된다. IL은 분리된 나무의 왼쪽 노드(node)의 사례들, IR은 오른쪽 노드의 사례들, I는 두 사례들의 합집합(IL∪IR)을 의미한다. gi는 손실함수에 대한 1차 경사 통계량(first order gradient statistic), hi는 손실함수에 대한 2차 경사 통계량(second order gradient statistic)을 의미한다.
| (16) |
Extra trees(ET)는 Geurts et al.[2006]이 제안한 의사결정나무 기반 앙상블 기계학습 알고리즘이다. 다른 앙상블 방법과 다르게 ET 알고리즘은 절단점(cut-point)을 임의로(random) 선택하여 노드를 분리하고 모든 학습 표본을 사용한다. 회귀 문제에서 나무의 예측은 최종 예측을 얻기 위해 산술 평균(arithmetic average)에 의해 합쳐진다. 편향(bias)과 분산(variance) 측면에서 ET 알고리즘은 약한 임의성(randomization)을 지닌 다른 앙상블 모델보다 더 크게 분산을 감소시킬 수 있다. 그리고 모든 학습 표본을 사용함으로써 편향을 최소화할 수 있다. 또한 노드 분리 절차의 단순함(simplicity)은 절단점을 최적화하는 다른 앙상블 모델보다 상수를 줄일 수 있다. 나무의 각 후보 특성(candidate attribute)을 임의로 분리하여 RF보다 임의성을 더욱 증가시킨다.
인공신경망(artificial neural network, ANN)은 인간의 뇌와 같이 뉴런(neuron)이라 불리는 연결 단위(connected unit)의 집합이다. 뉴런은 실수(real number)로 신호를 받아 다른 뉴런에 전달한다. 개별 뉴런의 출력은 입력의 가중 합(weighted sum)을 비선형 함수(i.e. 활성화 함수)로 계산하여 얻는다. 기본적인 구조로 입력층(input layer)에서 자료를 받아 은닉층(hidden layer)을 통과하여 출력층(output layer)에서 결과를 얻는다. 뉴런과 연결은 학습을 하면서 손실함수를 최소로 하는 방향으로 조정(i.e. 역전사, backpropagation)되는 가중치를 가지며 이 가중치는 뉴런의 연결 강도를 조절한다. Eq. 17에서 는 출력층 뉴런 k의 예측값, wkj는 출력층 뉴런 k와 은닉층 뉴런 j를 연결하는 가중치이다. hj는 은닉층의 출력으로 n은 은닉층 뉴런의 수를 의미한다. f는 출력층의 활성화 함수(activation function), bj는 출력층 뉴런 k의 편향(bias)이다.
| (17) |
극학습기계(extra learning machine, ELM)은 순방향 신경망(feedforward neural network) 학습 속도를 개선하기 위해 Huang et al.[2006]이 제안한 알고리즘이다. ELM은 단일 은닉층 순방향 신경망(single-hidden layer feedforward neural networks, SLFNs)의 은닉층 노드를 임의로 선택하고 출력 가중치를 결정한다. Eq. 18은 은닉층 노드의 수가 인 표준 SLFNs의 출력(tj)을 의미하며 xj는 입력, g는 활성화 함수, N은 표본의 수, wi는 i번째 은닉층 노드와 입력층 노드들을 연결하는 가중치 벡터(vector), βi는 i번째 은닉층 노드와 출력층 노드들을 연결하는 가중치 벡터, bi는 편향 벡터이다. wi·xj는 가중치 벡터와 입력 벡터의 내적을 의미한다.
| (18) |
ELM에서는 은닉층까지 출력을 행렬 H로 나타내면 Eq. 19와 같이 변형할 수 있다.
| (19) |
기존의 SLFNs와 달리 활성화 함수가 무한히 미분 가능(differentiable)하다면 입력 가중치(wi)와 은닉층 편향(bi)은 학습 초기에 고정시키고 Eq. 20과 같은 선형 모델의 최소자승해(least squares solution)인 를 구하는 것과 같아진다.
| (20) |
만약 표본의 수가 은닉층 노드의 수와 같다면 행렬 H는 정사각행렬(square matrix) 및 가역행렬(invertible matrix)이고 오차가 0에 근사한다. 하지만 보통 표본의 수가 은닉층 노드의 수보다 많아 행렬 H는 정사각행렬이 아니고 Hβ = T와 같이 wi, bi, βi가 존재하지 않는다. 최소 노름 최소자승해(minimum normleast-squares solution)는 Eq. 21과 같다. 여기서 H†는 행렬 H의 무어-펜로즈 유사역행렬(Moore-Penrose generalized inverse)이다. 이렇게 ANN의 가중치를 조정하기 위한 역전사 과정을 생략하고 신속하게 신경망을 최적화하여 오차를 줄일 수 있다.
| (21) |
퍼지신경망(neuro-fuzzy network, NFN)에서는 퍼지 논리(fuzzy logic)가 신경망(neural network)의 자료 기반 학습(data driven learning)에 의해 훈련된다. 퍼지는 불명확함(ambiguity)을 의미하며 Zadeh[1965]가 제안한 퍼지집합(fuzzy sets)에 의해 소속(membership)의 경계가 불명확한 경우 연속성(continuum)을 갖는 집합으로 표현한다. 퍼지집합에서 소속도(degree of membership)는 0과 1 사이의 값을 가진다. 퍼지추론(fuzzy inference)은 몇 개의 퍼지명제(fuzzy proposition)로부터 하나의 다른 근사적인 퍼지명제를 유도하는 방법을 말한다. 퍼지집합의 입력 원소(input element)들은 소속함수(membership function)를 통해 소속도로 나타내며 이를 퍼지화(fuzzification)라고 한다. 퍼지화 후 퍼지규칙(fuzzy rule)을 적용하여 입력변수와 출력변수 간의 관계를 정의해주고 퍼지추론엔진(fuzzy inference engine)으로 출력을 찾는다. 그리고 모든 출력을 통합하여 하나의 퍼지집합으로 나타낸다. 마지막으로 비 퍼지화(defuzzification) 출력을 등가의 정확한 값(crisp value)으로 변환한다.
퍼지화층(fuzzification layer)에서 Eq. 22와 같이 퍼지화를 위해 종모양(bell-shaped)의 소속함수를 사용하였다. 여기서 xi는 i번째 입력값, Rij(xi)는 j번째 퍼지규칙을 위한 i번째 입력값에 대한 소속 함수를 의미한다. a는 소속함수의 퍼짐 정도, b는 종의 형태, c는 중심값(centroid)을 나타내는 퍼지규칙의 조건부 계수(premise parameter)이다.
| (22) |
퍼지규칙층(fuzzy rule layer)에서는 Eq. 23을 이용하여 퍼지연산을 통해 RN개의 퍼지규칙의 호환성(compatibility)을 나타내는 firing strength를 계산한다(Buckley and Hayashi[1994]). Lk는 k번째 퍼지규칙 노드이다. 여기서 j는 k번째 퍼지규칙 노드에 대한 i번째 입력값의 퍼지 언어변수(fuzzy linguistic term)를 결정하는 번호(index)이다.
| (23) |
비 퍼지화층(defuzzification layer)에서는 입력자료들의 분류 결정 단계와 계수들의 최적화 단계로 구분된다. 분류 결정 단계에서는 각 퍼지규칙의 firing strength와 가중치의 선형 조합을 계산하여 퍼지규칙과 분류 클래스(class) 간의 적합도(matching degree)를 Eq. 24와 같이 계산한다. 여기서 wkl은 퍼지규칙층의 k번째 노드와 비퍼지화층의 l번째 노드 사이의 가중치를 의미한다.
| (24) |
그리고 비 퍼지화층의 활성화 함수로 클래스의 소속도(Eq. 25)를 출력한다. 여기서 Ol은 소속도, f는 활성화 함수를 의미한다.
| (25) |
최적화 단계에서는 앞서 얻은 소속도와 출력값과의 차이를 Eq. 26과 같이 계산한다.
| (26) |
오차를 최소화할 수 있을 때까지 Eq. 27-30과 같이 계수와 가중치를 최적화한다. 여기서 t는 최적화 차수, η는 학습률(learning rate)이다.
| (27) |
| (28) |
| (29) |
| (30) |
Jang[1993]이 제안한 적응형 퍼지신경 추론 모델(ANFIS)은 5개의 층으로 구성되어 있는 퍼지신경망이다. Takagi-Sugeno 퍼지규칙에 의해 출력함수를 Eq. 31과 같이 나타낼 수 있다(Takagi and Sugeno[1983]). x, y는 노드의 입력, Ai, Bi는 퍼지집합, pi, qi, ri는 출력함수의 결론부 계수(consequent parameter)이다.
| (31) |
첫 번째 층에서는 소속함수로 Eq. 32와 같이 각 노드의 입력에 대한 소속도를 구한다. 두 번째 층에서는 소속도를 입력 받아 소속도를 Eq. 33의 퍼지연산을 통해 퍼지규칙의 적합도를 구한다. 여기서 Oi는 층의 출력, μ(x)는 소속함수, wi는 퍼지규칙의 적합도(i.e. firing strength)이다.
| (32) |
| (33) |
세 번째 층에서는 각 노드에서 i번째 규칙의 적합도를 Eq. 34와 같이 정규화한다.
| (34) |
네 번째 층에서는 각 노드의 개별 규칙의 출력함수와 정규화된 적합도(normalized firing strength)를 Eq. 35와 같이 곱한다.
| (35) |
마지막 층은 단일노드로 구성되어 있고 모든 입력을 대상으로 출력을 Eq. 36과 같이 계산한다. 출력값은 연속형 값을 가진다.
| (36) |
조건부 및 결론부 계수를 최적화하기 위해 순방향 학습에서는 조건부 계수를 고정하고 결론부 계수를 최소화하기 위해 최소자승법을 사용한다. 역전사 학습에는 경사하강(gradient descent)법을 통해 조건부 계수를 최적화한다.
유전 알고리즘(genetic algorithm, GA)은 Holland[1984]가 제안한 생물학적 진화(evolution)를 모방한 진화 알고리즘(evolutionary algorithm)이다. 유전자(gene)가 구하려는 해일 때 유전자 간의 교배를 통해 최적의 해를 탐색한다. 구하려는 해를 유전자로 표현하는 초기화(initialization)를 한 뒤 각 유전자에 대해 적합도(fitness)를 계산한다. 그리고 다음 세대(generation)로 물려줄 유전자를 선택(selection)한다. 선택된 유전자들 간의 교차(crossover)를 통해 새로운 유전자를 형성한다. 후손 중 일부가 변이(mutation)를 일으켜 도태된다. 현재 세대의 유전자를 후손 유전자로 대치(replacement)해준다. 초기화-선택-교차-변이-대치의 유전 연산을 유전자가 더 이상 변하지 않을 때까지 반복한다. 그리고 최종 세대에서 가장 우수한 유전자를 해로 사용한다.
인공신경망에서는 가중치가 구하려는 해이므로 유전자로 설정한다. Eq. 37과 같이 초기 세대의 가중치를 초기화한다. 여기서 n은 초기 세대 가중치(유전자)의 수, Wn은 n번째 가중치, W는 초기 가중치, αn은 가우시안 분포(Gaussian distribution) 값이다. 가우시안 분포 값은 유전자에 임의값을 더해주어 유전자가 과도하게 변화하는 것을 방지한다.
| (37) |
선택 전략 중 순위 선택(ranking selection) 방법은 상위권의 적합도를 가지는 유전자를 선택한다. 개의 유전자 중 상위 N개의 유전자를 선택한다. 교차 연산에서는 전체 산술 재결합(whole arithmetic recombination) 방법을 사용하여 Eq. 38과 같이 후손(child) 유전자를 형성한다. 여기서 x, y는 부모(parent) 유전자, α는 0과 1 사이의 값이다. 교차를 통해 개의 후손 유전자를 만든다.
| (38) |
아주 작은 확률로 부모 유전자에 없는 유전자가 발현될 수 있는데 이는 교차 과정에서 불완전한 재결합에 의해 발생한다. 변이는 유전자를 임의적으로 변경해준다. 이후 변이된 유전자를 포함하여 개의 후손 유전자를 다음 세대로 물려준다. 이 과정을 반복하여 최적의 유전자(i.e. 가중치)를 찾아 인공신경망을 최적화한다.
2.4 교차검증 및 하이퍼파라미터 튜닝
이 연구는 XGBR, ETR, ANN의 최적 하이퍼파라미터(hyperparameter)를 탐색하기 위해 GridSearchCV라는 교차검증(cross validation, CV) 기반 하이퍼파라미터 튜닝(tuning) 방식을 사용하였다. 각 모델 별로 하이퍼파라미터 그리드(grid)를 구성하고 교차검증 시 폴드(fold) 수는 5로 설정하였다. 이외의 알고리즘 기반 모델은 기존 문헌에서 보고된 최적 하이퍼파라미터들을 대상으로 trial-and-error 방식으로 수정하여 학습하였다. 인공신경망 기반 모델의 손실함수는 회귀모델에 주로 사용되는 평균절대비오차(mean absolute percentage error, MAPE)로 설정하였다. Table 3은 이 연구에서 사용한 최적 하이퍼파라미터이다. 여기서 kernel은 커널함수, gamma는 커널 상수(kernel coefficient), C는 정규화 계수(regularization parameter), learning_rate는 학습률, n_estimator는 나무의 수, criterion은 노드 분리 품질(quality of split) 평가 기준, optimizer는 신경망 학습 최적화 방법, epochs는 전체 자료에 대한 학습 수, batch_size는 1 epochs에 사용되는 학습 표본 수, hidden_units은 은닉층 노드의 수, random_type은 가중치 초기화 방법, num_generation은 유전 알고리즘 세대수이다.
2.5 모델 성능 평가
이 연구는 모델의 WQI 예측성능을 평가하기 위해 기존 문헌에서 공통으로 사용한 평균 제곱근오차(root mean square error, RMSE), 평균절대오차(mean absolute error, MAE)를 평가지표(metrics)로 사용하였다(Li et al.[2019], Bui et al.[2020], Khozani et al.[2022]). 각 평가지표의 계산식은 Eq. 39-40과 같다.
| (39) |
| (40) |
이 연구의 WQI 모델 예측 방법을 Fig. 1에 도식화하였다.
3. 결과 및 고찰
3.1 실험결과
해양수질자동측정망 자료를 보정한 결과 부산수영 5개(Temp_Sur, DO_Sur, TP_Sur, NH3-N_Sur, DIP_Sur(PO4-P_Sur)), 광양적량 4개(Temp_Sur, DO_Sur, Salinity_Sur, COD_Sur), 인천송도 4개(Temp_Sur, DO_Sur, TN_Sur, NH3-N_Sur), 마산삼귀 7개(Temp_Sur, pH_Sur, DO_Sur, Chl-a_Sur, TP_Sur, NO3-N_Sur, DIP_Sur(PO4-P_Sur)), 시화반월 5개(Temp_Sur, DO_Sur, Salinity_Sur, Chl-a_Sur, TN_Sur), 시화조력 6개(Temp_Sur, DO_Sur, Chl-a_Sur, TP_Sur, DIP(PO4-P_Sur), SS_Sur(Turbidity_Sur))의 변수를 선택하여 자료를 학습에 사용하였다. 모든 해역에서 공통으로 선택된 변수는 Temp_Sur, DO_Sur이다. 해양수질자동측정망 자료의 이상치 제거 후 변수 간결정계수를 비교한 결과 해양환경측정망 자료에 대한 해양수질자동측정망 자료의 설명력은 모든 측정소에서 Temp_Sur이 가장 컸다(R2:0.87−0.99). 해역별로 비교하면 마산삼귀 측정소에서 가장 컸다(R2:0.994). 다음 순서로 DO_Sur이 컸으나 해역별로 편차가 컸다(R2:0.27−0.75). 해역별로 비교하였을 때 인천송도 측정소에서 가장 컸다(R2:0.748). 이외 변수들은 해역별로 결정계수가 매우 상이하였다.
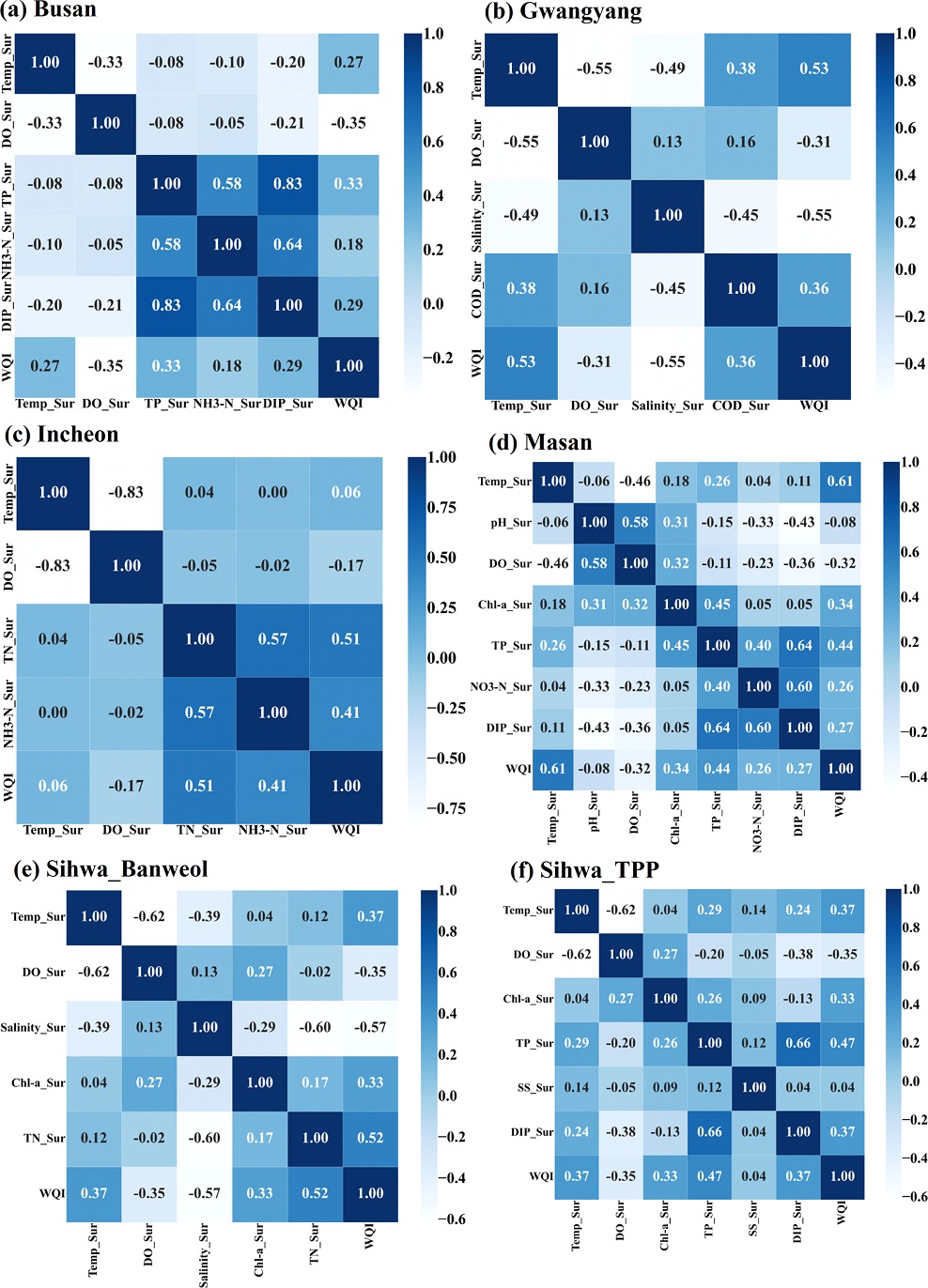
훈련자료인 해양환경측정망 자료에서 해역별로 선택된 입력변수와 WQI의 상관관계(correlation)는 Fig. 2와 같다. 부산연안(Busan) 자료에서는 DO_Sur, TP_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2a). 광양만(Gwangyang) 자료에서는 Salinity_Sur, Temp_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2b). 인천연안(Incheon) 자료에서는 TN_Sur, NH3-N_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2c). 마산만(Masan) 자료에서는 Temp_Sur, TP_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2d). 시화반월(Sihwa_Banweol) 자료에서는 Salinity_Sur, TN_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2e). 시화조력(Sihwa_TPP) 자료에서는 TP_Sur, Temp_Sur, DIP_Sur과 WQI가 강한 상관관계를 보였다(Fig. 2f). 해역별로 입력변수와 WQI의 상관관계는 상이하였다. WQI 계산에 사용되는 변수인 Chl-a_Sur, DIP_Sur은 WQI와 약한 상관관계를 보였다.
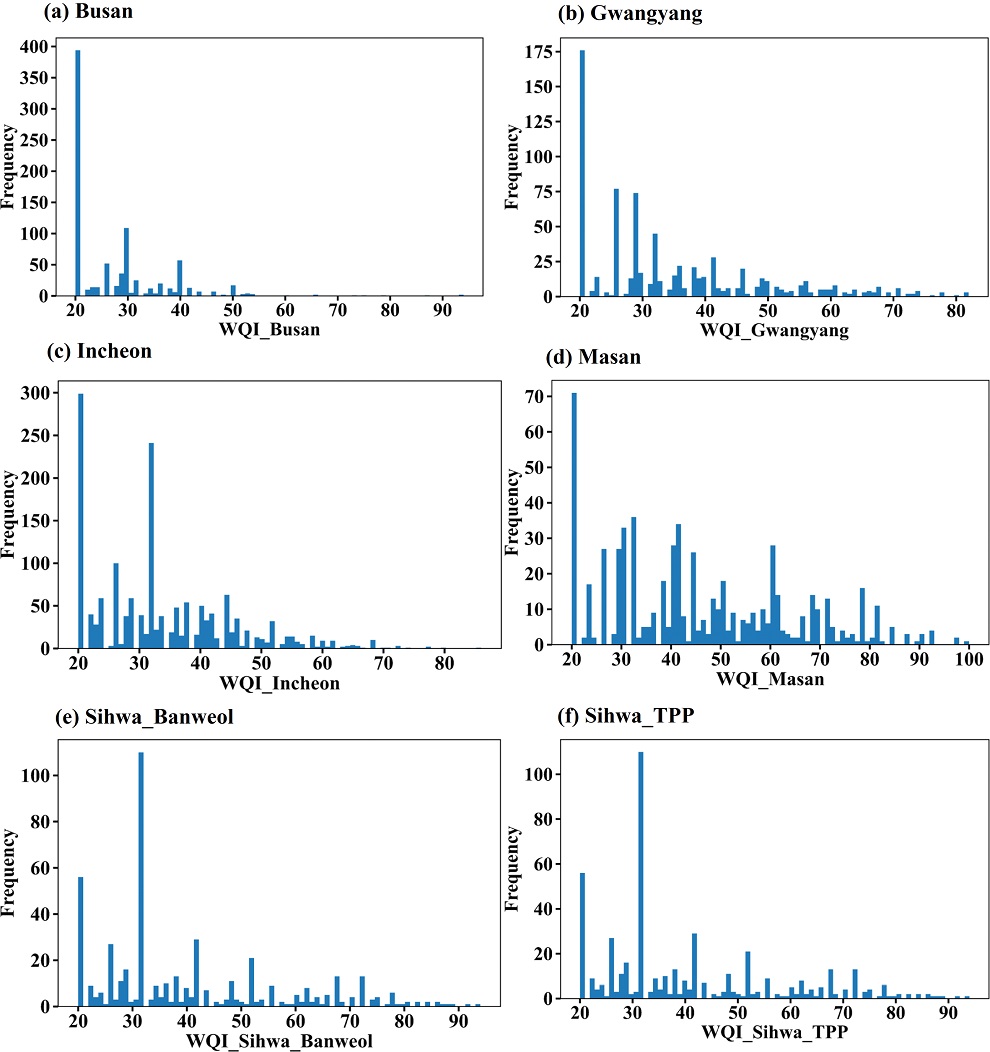
해역별 훈련자료 중 WQI의 분포는 Fig. 3과 같다. 마산만의 경우 다른 해역에 비해 WQI가 큰(수질이 나쁜) 자료의 비율이 높았다(Fig. 3d). 부산연안, 광양만, 인천연안은 WQI 20 초반 값이 가장 많았고 다음으로 WQI 20 후반 또는 30 초반의 자료가 많았다(Fig. 3a-c). 시화호는 WQI 30 초반 자료가 가장 많았고 다음으로 WQI 20 초반 자료가 많았다(Fig. 3e-f). 자료의 수와 WQI 분포를 고려할 때 부산연안의 수질이 가장 좋은 것으로 판단된다.
MLR, SVR, XGBR, ETR, ANN, ELM, NFN, ANFIS, GANN 알고리즘 기반 WQI 예측 모델의 WQI 예측성능을 평가·비교했다. 최적 하이퍼파라미터로 학습한 개별 모델의 예측성능은 Table 4와 같다. 부산수영 측정소에서는 SVR, 광양적량 측정소는 ELM, 인천송도와 마산삼귀 측정소는 ETR, 시화반월 측정소는 RMSE 기준 GANN, MAE 기준 ANFIS, 시화조력 측정소는 RMSE 기준 SVR, MAE 기준 ANFIS 모델의 WQI 예측성능이 가장 우수하였다. MAE보다 RMSE가 큰 오차에 덜 민감하여(robust) 비교하기 유리하다.
측정소 별로 결과를 비교하였을 때 MLR, SVR, XGBR, ETR, ANN, ELM 모델은 시화반월 측정소에서 예측 오차가 가장 크게 나타났고 퍼지논리 기반의 인공신경망(NFN, ANFIS) 모델은 마산 삼귀 측정소, 유전 알고리즘 기반 인공신경망(GANN) 모델은 시화 조력 측정소에서 오차가 가장 컸다. 이 연구 결과에서는 측정소 별로 훈련자료와 평가자료의 수에 차이가 있어 특정 알고리즘 모델의 예측 오차에 대한 비교보다는 개별 측정소에 적합한 WQI 예측 알고리즘을 선별하고자 한다.
해역별 모델의 예측값(predicted value)과 실제값(true value) 간의 시각적 비교는 Fig. 4와 같다. 부산수영 측정소의 모델 WQI 예측 결과 의사결정 나무 기반 앙상블 모델인 XGBR, ETR 모델은 WQI를 과대평가(overestimate)하여 예측하는 경향이 있었다(Fig. 4a). 이외 모델은 실제 WQI가 40인 자료는 WQI를 과소평가(underestimate)하여 예측하였고 실제 WQI가 26, 35인 자료는 과대평가하는 경향을 보였다. 실제 WQI와 모델에 따라 예측성능이 매우 상이하였다. 성능이 가장 우수한 SVR 모델은 중간 수준의 WQI(30, 36)는 근사하게(approximately) 예측을 하였으나(오차율<3%), 최대값(40), 최소값(26)에서는 큰 오차를 보였다(오차율>15%). SVR은 실제 높은 수준의 WQI를 가진 자료의 WQI 예측성능이 낮은 것으로 판단된다. 오히려 실제 WQI 최대값에서는 앙상블 모델이나 ELM 모델의 예측값이 실제값에 더 근접하였다.
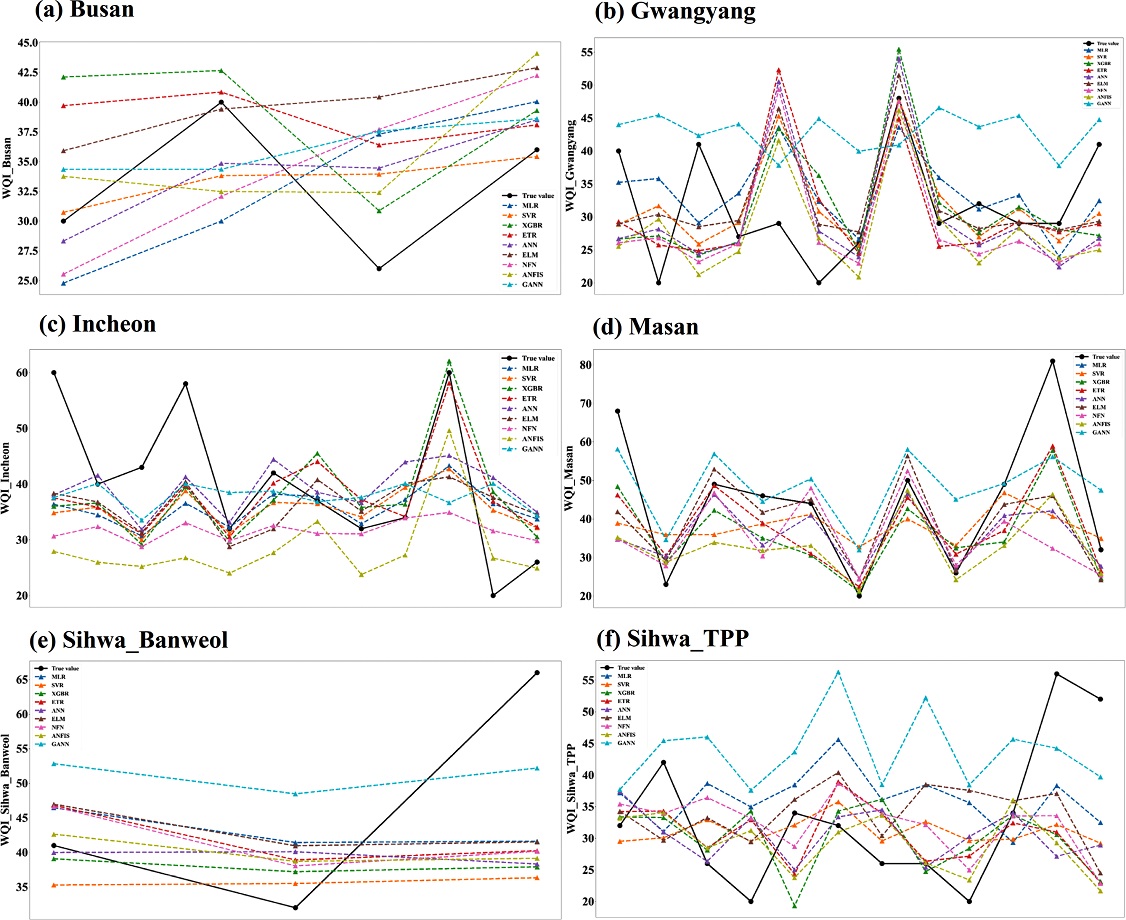
Time variation plot for predicted and true values in testing phase with water quality datasets observed by each station(Black solid line means true values and dash lines colored as blue(MLR), orange(SVR), green(XGBR), red(ETR), purple(ANN), brown(ELM), pink (NFN), olive(ANFIS), and cyan(GANN) are for predicted values by each model).
광양적량 측정소의 모델 WQI 예측 결과 실제 WQI가 매우 낮은 자료(20)에 대해 모든 모델에서 WQI를 과대평가하여 예측하였다(Fig. 4b). 이 경우 좋은 수질이 나쁘게 판단될 수 있는 오류를 범할 수 있다. 반대로 최대값(48)에서는 XGBR, ANN, GANN 모델을 제외하고 예측 오차가 작았다(오차율<10%). 실제 WQI가 높은 시기에는 보정 후 선택한 변수의 자료만으로 WQI를 예측할 수 있다고 판단된다. 성능이 가장 우수한 ELM 모델은 실제 WQI 29, 48인 일부 자료에서는 근사하게 예측하였으나(오차율<8%), 예측의 일관성(consistency)이 부족하였다.
인천송도 측정소의 모델 WQI 예측 결과 실제 WQI가 40보다 높은 자료는 WQI를 과소평가하여 예측하는 경향을 보였다(Fig. 4c). 반대로 30미만의 실제 WQI를 가진 자료는 과대평가하여 예측하는 경향을 보였다. 예측성능이 가장 우수한 ETR 모델은 실제 WQI가 높은 자료(58-60)에서 예측의 일관성이 부족하였다.
마산만은 타 해역보다 수질이 나쁜(WQI가 높은) 해역이다(Fig. 3d). 그러므로 WQI가 높은 시기의 실시간 수질 감시가 중요하다. 하지만 마산삼귀 측정소의 모델 중 가장 우수한 ETR 모델은 실제 WQI가 높은 자료(60 이상)에 대해 예측성능이 낮았다(Fig. 4d). 실제 WQI가 49인 자료에 대해서는 예측 오차가 매우 작았다(오차율: 0.7%). 하지만, 예측의 일관성이 부족하였다.
시화반월 측정소의 WQI 예측 모델은 실제 WQI 최대값(66)인 자료의 WQI를 과소평가하여 예측하였다(Fig. 4e). 성능이 가장 우수한 GANN 모델에서도 큰 예측 오차를 보였다(오차율>20%).
시화조력 측정소에서는 실제 WQI 최대값(56)인 자료는 모든 모델이 WQI를 과소평가하여 예측하였다(Fig. 4f). 성능이 가장 우수한 SVR 모델도 높은 수준의 실제 WQI에서는 과소평가하여 예측하였다. 반면 실제 WQI가 26-34인 구간에서는 비교적 오차가 작았다(오차율<14%).
3.2 고찰
모델 예측 결과 해역별로 실제 WQI가 높은 구간에서는 예측성능이 낮고 일관성이 부족하였다. 부산수영과 광양적량 측정소의 경우 WQI 수준에 따라 예측성능이 상이하므로 조사 시기별 수질 특성에 따라 다른 모델을 사용하여 예측하는 방법도 고려할 수 있다.
마산삼귀 측정소 모델에서는 가장 많은 변수를 선택하여 학습하였고 WQI 계산에 필요한 변수(Chl-a_Sur, DIP_Sur)를 포함하고 있다. 그리고 훈련자료 중 WQI가 높은 수질 자료가 가장 많았다(Fig. 3d). 선택된 변수보다는 모델의 구조와 WQI 분산(variance)이 WQI 예측성능에 영향을 주는 것으로 보고하였다(Asadollah et al.[2021]; Tiyasha et al.[ 2021]). 하지만, 예측성능은 타 해역에 비해 우수하지 않았고 심지어 수질이 나쁜 시기에도 예측성능이 낮았다(Fig. 4d). 예측성능이 가장 우수한 모델(ETR)에서 실제 WQI 49인 자료에 대해 수온이 높은 8월에는 예측 오차가 매우 작았으나(오차율 : 0.7%) 수온이 상대적으로 낮은 11월에는 오차가 매우 큰(오차율 : 24.4%) 경향을 보였다. 마산삼귀 측정소 자료에서 표층 수온(Temp_Sur) 자료는 이상치 제거 후 해양환경측정망 자료에 대한 설명력이 가장 높았고(결정계수 값이 크고), 해양환경측정망 자료에서도 Temp_Sur이 WQI와 가장 강한 상관관계를 보였다(Fig. 2d). 그러므로 마산삼귀 측정소의 WQI 예측성능은 Temp_Sur에 영향을 받는 것으로 판단된다.
이와 유사하게 인천송도 측정소에서도 예측성능이 가장 우수한 모델(ETR)에서 실제 WQI 60인 자료에 대해 일관성이 부족한 예측을 보였다. 2018년 8월 자료에서는 예측 오차가 작았으나(오차율 : 3.1%), 2021년 8월 자료에서는 예측 오차가 매우 컸다(오차율 : 37.5%). 인천송도 측정소 자료에서 Temp_Sur, DO_Sur 자료는 해양환경측정망 자료에 대한 설명력이 높았으나 질소(TN_Sur, NH3-N_Sur) 자료는 설명력이 낮아 질소 자료에 대한 보정 정확도가 낮을 것으로 판단된다. 반면, 해양환경측정망 자료에서는 질소 자료가 상대적으로 WQI와 강한 상관관계를 보였다(Fig. 2c). 결과적으로 인천송도 측정소의 WQI 예측 모델이 수질이 악화되는 시기에 민감도가 낮을 것으로 판단된다.
이 연구에서는 해역별로 모든 정점의 해양환경측정망 자료를 모델 훈련에 사용하였다. 정점별로 수질 자료가 상이할 뿐만 아니라 심지어 수질이 좋은 자료가 더 많았다(Fig. 3). 하지만 해양수질자동측정망은 특별관리해역 중 환경변화에 대한 집중감시가 필요한 지역에서 운영하며 인근 해양환경측정망 정점은 수질의 변동이 심하고 수질 자료가 비선형성을 갖기 때문에 자료의 패턴(pattern)을 학습하기 어렵다. 그러므로 오염의 우려가 있고 수질이 나쁜(WQI가 높은) 해양수질자동측정망 정점의 수질 자료의 패턴을 훈련하기에 자료가 충분하지 않다고 판단된다. 반면, 해양수질자동측정망 인근 정점만을 훈련자료로 활용할 경우 수질 자료의 수가 부족하여 모델의 예측이 불안정할 수 있다. 향후 수질 자료가 축적된다면보다 성능이 개선된 모델로 오염우심지역의 WQI를 예측할 수 있을 것이다. 자료의 결여(scarcity) 문제를 해결하기 위해 수질이 나쁜 자료만을 이용하여 합성 데이터(synthetic data)를 생성하여 모델 훈련에 사용하는 방법도 고려할만하다.
WQI를 계산하기 위해서 저층 DO를 사용하고 있다. 이전 연구에서도 DO는 WQI 예측에 가장 중요한 인자라고 보고된 바 있다(Hameed et al.[2017]; Kim et al.[2022]). 하지만 해양수질자동측정망은 저층 DO 자료를 제공하지 않아 이 연구에서는 표층 DO 자료를 이용하여 WQI를 예측한다는 한계점을 가지고 있다.
또한 모델의 학습 성능이 좋더라도 보정의 품질(quality)이 낮으면 정확한 예측이 어렵다. 이 연구에서는 해양환경측정망 자료와 해양수질자동측정망 자료의 개별 수질 항목에 대한 선형회귀를 통해 얻은 레버리지와 잔차를 동시에 고려한 Cook의 거리로 이상치를 판단하여 제거하고 최적의 선형회귀 모델을 통해 값을 보정하였다. 하지만 Cook의 거리는 일부 관측이 투영행렬에 미치는 영향을 왜곡(distort)할 수 있어 항상 정확하게 이상치를 판단하는 것은 아니다(Kim et al.[2017]). 대안으로 isolation forest, local outlier factor 등과 같은 통계 기반 자동화 이상치 탐지(automatic anomaly detection)방법을 사용하여 이상치를 제거할 수 있다. 또한 해양환경측정망 자료와 해양수질자동측정망 자료 간의 선형적인 보정이 아닌 비선형 모델을 이용한 보정도 고려할 수 있다.
4. 결 론
이 연구에서는 특별관리해역에서 운영하고 있는 해양수질자동측정망(부산수영, 광양적량, 마산삼귀, 인천송도, 시화반월, 시화조력) 자료를 해양환경측정망 자료를 이용하여 보정하였다. 보정한 자료의 품질에 따라 학습에 사용할 변수를 선택하였다. 선택된 변수의 해양환경측정망(부산연안, 광양만, 마산만, 시화호, 인천연안) 자료를 다양한 알고리즘(MLR, SVR, XGBR, ETR, ANN, ELM, NFN, ANFIS, GANN) 기반 모델로 훈련하였다. 그리고 보정한 해양수질자동측정망 자료의 WQI를 예측하여 훈련된 모델을 평가하였다. 모델 성능 평가 결과 해역별로 WQI가 높은 구간에서는 예측성능이 낮고 일관성이 부족하였다. 훈련용 타깃 자료의 클래스 불균형(imbalance), 측정 불확실성(measurement uncertainty), 자료의 결여, 미흡한 보정 품질이 예측성능 저하의 원인으로 판단된다. 자료의 양과 질을 고려하고 보정방식을 보완하여 모델을 학습한다면 예측성능을 개선할 수 있다고 판단된다. 또한 부영양화 이외의 해양환경 문제(빈산소, 고수온, 오염물질 방류 등)와 관련된 변수도 고려한다면 실시간으로 해양환경을 감시하여 해양오염사고를 예측하고 대응할 수 있을 것이다. 현장에서 센서를 통해 실시간으로 수집한 수질 자료를 이용하여 학습된(data-driven) 모델로 즉각적으로 예측하는 것이 기존 모델(i.e. process-based model)보다 의사결정(decision-making) 시간을 단축할 수 있다(Mohammed et al.[2022]).
Acknowledgments
이 논문은 2022년도 정부(해양수산부)의 재원으로 해양수산과학기술진흥원-해양유해물질오염원 추적기법개발 사업 지원을 받아 수행된 연구임(KIMST-20220534).
References
-
Abba, S.I., Abdulkadir, R.A., Sammen, S.S., Pham, Q.B., Lawan, A.A., Esmaili, P., Malik, A. and Ansari, N.A., 2022, Integrating feature extraction approaches with hybrid emotional neural networks for water quality index modeling, Applied Soft Computing, 114, 108036.
[https://doi.org/10.1016/j.asoc.2021.108036]

-
Abba, S.I., Hadi, S.J., Sammen, S.S., Salih, S.Q., Abdulkadir, R.A., Pham, Q.B. and Yaseen, Z.M., 2020, Evolutionary computational intelligence algorithm coupled with self-tuning predictive model for water quality index determination, Journal of Hydrology, 587, 124974.
[https://doi.org/10.1016/j.jhydrol.2020.124974]

-
Asadollah, S.B.H.S., Sharafati, A., Motta, D. and Yaseen, Z.M., 2021, River water quality index prediction and uncertainty analysis: A comparative study of machine learning models, Journal of Environmental Chemical Engineering, 9(1), 104599.
[https://doi.org/10.1016/j.jece.2020.104599]

-
Buckley, J.J. and Hayashi, Y., 1994, Fuzzy neural networks: A survey, 66, 1-13.
[https://doi.org/10.1016/0165-0114(94)90297-6]

-
Bui, D.T., Khosravi, K., Tiefenbacher, J., Nguyen, H. and Kazakis, N., 2020, Improving prediction of water quality indices using novel hybrid machine-learning algorithms, Science of The Total Environment, 721, 137612.
[https://doi.org/10.1016/j.scitotenv.2020.137612]

-
Chen, T. and Guestrin, C., 2016, XGBoost: A scalable tree boosting system, KDD '16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785-794.
[https://doi.org/10.1145/2939672.2939785]

-
Cook, R.D., 1977, Detection of Influential Observations in Linear Regression, TECHNOMETRICS, 19(1).
[https://doi.org/10.2307/1268249]

-
Gazzaz, N.M., Yusoff, M.K. Aris, A.Z., Juahir, H. and Ramli, M.F., 2012, Artificial neural network modeling of the water quality index for Kinta River (Malaysia) using water quality variables as predictors, Marine Pollution Bulletin, 64(11), 2409-2420.
[https://doi.org/10.1016/j.marpolbul.2012.08.005]

-
Geurts, P., Ernst, D. and Wehenkel, L., 2006, Extremely randomized trees, Mach Learn, 63, 3-42
[https://doi.org/10.1007/s10994-006-6226-1]

-
Hameed, M., Sharqi, S.S., Yaseen, Z.M., Afan, H.A., Hussain, A. and Elshafie, A., 2017, Application of artificial intelligence (AI) techniques in water quality index prediction: a case study in tropical region, Malaysia, Neural Comput & Applic 28(Suppl 1), 893–905.
[https://doi.org/10.1007/s00521-016-2404-7]

- Holland, J.H., 1984, Genetic Algorithms and Adaptation. In: Selfridge, O.G., Rissland, E.L., Arbib, M.A. (eds) Adaptive Control of Ill-Defined Systems. NATO Conference Series, vol 16. Springer, Boston, MA.
-
Huang, G.B., Zhu, Q.Y. and Siew, C.K., 2006, Extreme learning machine: Theory and applications, Neurocomputing, 70, 489-501.
[https://doi.org/10.1016/j.neucom.2005.12.126]

-
Jang, J.S.R., 1993, ANFIS : Adaptive-Network-Based Fuzzy Inference System, IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS, 23(3).
[https://doi.org/10.1109/21.256541]

-
Jeon, S.B., Oh, H.Y. and Jeong, M.H., 2020, Estimation of Sea Water Quality Level Using Machine Learning, Journal of Korean Society for Geospatial Information Science, 28(4), 145-152.
[https://doi.org/10.7319/kogsis.2020.28.4.145]

-
Khan, M.S.I., Islam, N., Uddin, J., Islam, S., and Nasir, M.K. 2022, Water quality prediction and classification based on principal component regression and gradient boosting classifier approach, Journal of King Saud University - Computer and Information Sciences, 34(8), Part A, 4773-4781.
[https://doi.org/10.1016/j.jksuci.2021.06.003]

- Khozani, Z.S., Iranmehr, M. and Mohtar, W.H.M.W., 2022, Improving Water Quality Index Prediction for Water Resources Management plans in Malaysia: Application of Machine Learning Techniques, Geocarto International.
-
Kim, M.G., 2017, A cautionary note on the use of Cook’s distance, Communications for Statistical Applications and Methods, 24(3), 317-324.
[https://doi.org/10.5351/CSAM.2017.24.3.317]

- Kim, S.B., Lee, J.S. and Kim, K.T., 2022, WQI Class Prediction of Sihwa Lake Using Machine Learning-Based Models, J. Korean Soc. Oceanogr., 27(2), 71-86.
-
Kouadri, S., Elbeltagi, A., Islam, A.R.M.T. and Kateb, S., 2021, Performance of machine learning methods in predicting water quality index based on irregular data set: application on Illizi region (Algerian southeast), Appl Water Sci, 11(190).
[https://doi.org/10.1007/s13201-021-01528-9]

-
Kulisz, M., Kujawska, J., Przysucha, B. and Cel, W., 2021, Forecasting Water Quality Index in Groundwater Using Artificial Neural Network, Energies, 14(18), 5875.
[https://doi.org/10.3390/en14185875]

- Learning-Based Models, J. Korean Soc. Oceanogr, 27(2), 71-86.
- Lee, G.H., Park, J.H., Ha, H.K., Kim, D.W., Lee, W.J., Kim, H.T. and Shin, H.J., 2018, Methodology on e-Navigation-Assisted Ocean Monitoring and Big Data Analysis, J. Korean Soc. Oceanogr., 23(4), 204-217.
-
Li, J., Abdulmohsin, H.A., Hasan, S.S., Kaiming, L., Khateeb, B.A., Ghareb, M.I. and Mohammed, M.N., 2019, Hybrid soft computing approach for determining water quality indicator: Euphrates River. Neural Comput & Applic 31, 827-837.
[https://doi.org/10.1007/s00521-017-3112-7]

-
Mohammed, H., Tornyeviadzi, H.M. and Seidu, R., 2022, Emulating process-based water quality modelling in water source reservoirs using machine learning, Journal of Hydrology, 609, 127675.
[https://doi.org/10.1016/j.jhydrol.2022.127675]

-
Park, S. and Lee, S.R., 2013, Marine Disasters Prediction System Model Using Marine Environment Monitoring, The Korean Institute of Communications and Information Sciences, 38(3).
[https://doi.org/10.7840/kics.2013.38C.3.263]

-
Smola, A.J. and Scholkopf, B., 2004, A tutorial on support vector regression, Statistics and Computing, 14, 199-222.
[https://doi.org/10.1023/B:STCO.0000035301.49549.88]

-
Takagi, T. and Sugeno, M., 1983, Derivation of Fuzzy Control Rules from Human Operator’s Control Actions, IFAC Proceedings Volumes, 16(13), 55-60.
[https://doi.org/10.1016/S1474-6670(17)62005-6]

-
Tiyasha, T.M. Tung and Z.M. Yaseen, 2021, Deep Learning for Prediction of Water Quality Index Classification: Tropical Catchment Environmental Assessment, Natural Resources Research, 30(6), 4235-4254.
[https://doi.org/10.1007/s11053-021-09922-5]

-
Yaseen, Z.M., Ramal, M.M., Diop, L., Jaafar, O., Demir, V. and Kisi, O., 2018, Hybrid Adaptive Neuro-Fuzzy Models for Water Quality Index Estimation. Water Resour Manage 32, 2227-2245.
[https://doi.org/10.1007/s11269-018-1915-7]

-
Zadeh, L.A., 1965, Fuzzy sets, INFORMATION AND CONTROL, 8, 338-353.
[https://doi.org/10.1016/S0019-9958(65)90241-X]