KOEM 해양환경측정망 자료를 이용한 평균 추정오차 분석
초록
최근 5년(2017-2021) 동안의 KOEM 해양환경측정망 자료를 이용하여 평균과 표준편차에 대한 신뢰구간 분석-평가를 수행하였다. 분석에 사용한 항목은 Secchi 수심(m), 총무기질소(TIN)와 총무기인(TIP), 엽록소, DO 농도(mg/L)이다. 매년 자료를 이용하여 평균, 표준편차의 95% 신뢰구간을 추정한 결과, 평균과 표준편차의 신뢰구간 범위의 평균은 저층 DO 항목의 경우 5.45-10.81, 0.96-6.29, Secchi Depth 항목은 1.80-6.46, 0.83-5.46 범위로 산정되었다. 이 신뢰구간은 평균대비 ±33%, ±56% 정도로 그 크기가 상당한 수준이다. 허용 가능한 신뢰구간을 ±10% 정도 이하 수준으로 가정하는 경우, 요구되는 자료의 개수는 각각 최소 20, 51개로 추정되었다. 한편 표준편차의 상한 신뢰구간 크기도 1.5배 이하로 저감하기 위해서는 최소 18개 정도의 자료가 필요한 것으로 파악되었다.
Abstract
Analysis and evaluation of the confidence interval (CI) of the mean and standard deviation (SD) were carried out using the KOEM marine environment monitoring network data for the last five years (2017-2021). The water quality parameters used for the analysis were Secchi depth(m), total inorganic nitrogen and phosphorus (TIN, TIP), chlorophyll-a, and bottom DO (mg/L) concentrations. As a result of the estimation using the annual data, the average ranges of the 95% CI of the mean and SD estimated for all years were 5.45-10.81, 0.96-6.29 for the bottom DO concentration and 1.80-6.46, 0.85-5.46 for the Secchi depth, respectively. These CIs are substantially large, corresponding to ±33% and ±56% of the mean. In the case of the condition of an acceptable CI of ±10%, the required minimum numbers of the data were estimated to be 20 and 51, respectively. On the other hand, it was found that at least 18 data were needed to reduce the size of the upper limit of the SD to 1.5 times or less.
Keywords:
Marine environment monitoring network, Confidence interval, Mean, Standard deviation, Tolerable limits키워드:
해양환경측정망, 신뢰구간, 평균, 표준편차, 허용가능 범위1. 서 론
해양환경측정망은 우리나라 연안해역의 환경상태에 대한 조사를 정기적으로 실시하여 환경현황을 종합적으로 파악하고, 국가해양환경관리 및 보전정책 수립을 위한 국가기본자료로의 활용을 목적으로 운영되고 있다(Marine Environmental Information System[2021]). 환경현황에 대하여 종합적으로 파악된 정보는 국가 정책에 직접적으로 반영되는 중요한 정보이며, 수질평가지수(WQI, water quality index, 해양수산부 고시, 제2018-10호, 2018.01.23.)가 종합평가를 위한 대표적인 정보로 사용되고 있다. 다양한 해양환경정보를 이용하는 이 통합과정은 통계적인 관점에서 하나의 표본에 해당하는 관측자료를 조합하여 이용하는 방법이다. 이 방법은 하나의 대표 지수(수치)로 해양환경을 판단하기 때문에 간단하지만, 현장 관측자료가 가지는 변동성분, 불확실성(uncertainty)에 대한 기본정보가 제외되는 단점이 있다. 추정정보의 불확실성은 환경현황을 종합적으로 판단하는 지수의 오차구간(신뢰구간, confidence interval)에 직접적인 영향을 미치기 때문에, 현재 수행되는 연4회 관측빈도 조건에서의 추정오차에 대한 종합적인 검토가 필요하다.
우리나라 연안의 수질환경 변동양상 분석연구는 수질항목의 상관관계, 추세, 장기 변동 양상 등을 중심으로 다양한 기간, 다양한 지점의 자료를 이용하여 수행되어 왔다(Nam et al.[2012]; Kim et al.[2012]; Lee & Oh[2006]; Kim et al.[2011]; Kwon[2010]; Kwon et al.[2013]; Park et al.[2022]). 그러나 자료의 관측기간, 정점, 분석시기 등의 차이로 우리나라 전체 해역에 대한 비교분석은 곤란한 상황이다. 또한, 통계적인 확률변수의 관점에서 통계측도(statistical measures)로 대표되는 평균, 표준편차 등에 대한 추정오차는 추정으로 제한되고, 정량적인 분석에 대한 연구는 매우 미흡한 실정이다. 신뢰수준에 상응하는 신뢰구간(오차구간)은 통계적인 검정에 이용되는 매우 중요한 정보임에도 불구하고, 구간추정(interval estimation)은 제외되고 점 추정(point estimation, 하나의 대표 수치로 결정되는 통계정보)만을 이용하고 있는 상황이다. 점 추정 정보만을 이용하는 경우, 통계적으로 의미가 없는 경우, 또는 통계적으로 유의미한 조건에 대한 판단이 오류를 발생시키기 때문에 적절한 환경현황 파악 및 정책수립에 제약이 따른다. 더불어, 생태기반 수질평가 및 기준개정 등에 관한 연구(Jeong et al.[2018]; Park et al.[2019])도 수행되는 상황에서 현재 해양환경측정망 자료의 통계적인 추정오차에 대한 연구도 중요한 사안으로 부각되고 있다.
본 연구에서는 우리나라 전체 해역을 포함하는 해양환경측정망 자료를 이용하여 대표적인 통계측도에 해당하는 평균(mean)과 표준편차에 대한 신뢰구간 추정 평가를 수행하고, 추정 신뢰구간의 크기를 분석하고, 비교평가를 수행하였다. 수질항목의 연(annual)평균 자료는 해양 환경관리 정책수립/평가의 중요한 지표로 이용되는 통계 측도(statistical measures)에 해당하며, 표준편차는 평균의 신뢰구간 추정에서 요구되는 통계측도이다. 따라서 본 논문에서는 평균, 표준편차 항목에 중점을 두고 추정을 수행한다. 더불어 현재 관측빈도를 유지하는 경우, 불가피하게 받아들여야만 하는 평균과 표준편차의 “신뢰구간”의 크기를 제시하고, 추정 불확실도(uncertainty level)에 해당하는 오차 구간의 크기를 실질적으로 허용가능한 수준을 가정하여 신뢰구간 분석에 사용된 수질항목의 “허용가능한 오차”를 제안한다.
2. 재료 및 방법
2.1 해양환경측정망 자료
해양환경측정망 자료는 1997년부터 2021년까지, 연 4회(2월, 5월, 8월, 11월) 측정한 자료로 2022년 기준, 총 375개 정점에서 관측을 수행하고 있으며, 관측항목은 총 16개이다(Secchi Depth 항목과 수온, 염분, pH, DO, COD, NH3, NO2, NO3, TIN(=NH3+NO2+NO3), TN, PO4(TIP), TP, SiO4, SS, chlorophyll-a 항목). Secchi Depth 항목을 제외한 모든 항목은 표층-저층의 자료로 구분된다. 관측정점은 항만, 연안, 하천영향 및 반폐쇄성해역, 연안, 근해로 구분되고 있다. 본 연구에서는 관측빈도가 일정하게 유지되고, 장기간의 자료가 가용한 연안, 하천영향 및 반폐쇄성 해역의 자료를 대상으로 분석을 수행하였다. 또한 관측정점의 개수를 일정하게 유지하기 위하여 최근 5년(2017-2021) 자료로 기간을 선정하였다. 항만관측은 연2회(2월, 8월) 수행, 근해는 연1회(8월) 관측 수행으로 관측빈도를 일정하게 유지하기 위하여 제외하였다.
해양환경측정망 자료는 원본자료로 제공되는 전산파일을 이용하였다. 원본자료는 해양환경정보포털(https://www.meis.go.kr/ → 해양관측 & 정도관리 → 해양환경관측 & 조사 → 해양환경측정망정보 → 원본자료)에서 다운로드가 가능하다. 다운로드 받은 파일은 정적자료(관측위치, 수심 등)와 동적자료(관측자료)로 구분하였으며, 동적 자료는 지점-항목-관측시기로 구분되는 행렬 형태로 변형하여 본 연구에서의 분석에 이용하였다.
수온, 염분 항목 기준으로 파악한 관측정점 개수는 1997년 209개, 2000년 230개, 2004년 263개, 2006년 269개, 2009년 279개, 2011년 282개, 2013년 317개, 2014년 347개, 2015년 367개, 2017년부터 현재까지 375개를 계속 유지하고 있다. 현재 관측정점 개수는 1997년, 2000년 기준 각각 1.79배, 1.63배 증가한 반면, 관측 빈도는 연 4회(관측시기도 2, 5, 8, 11월로 거의 고정)로 변함없이 유지되고 있는 상황이다.
관측정점은 정점번호(1-375)만으로도 개략적인 위치를 파악할 수 있도록 동해북단에서 시계방향으로 다시 정렬하였다. 새로 정렬된 정점번호 조건에서 현재 5개로 구분되는 생태구역의 범위는 동해 1-62(거진-구룡포, 정점개수=62), 대한해협 63-220(감포-가막만, 정점 개수=158), 서남해역 221-270(여자만-함평만, 정점개수=50), 서해중부(해역) 271-356(고창-인천, 정점개수=86), 제주 357-375(제주-한림, 정점개수=19)이다. 해역으로 구분하는 경우, 동해는 1-91(거진-기장), 남해동부해역(경상남도 남부해역, 부산–남해, 92-188), 남해서부해역, 섬진강(하구)-해남만, 189-253, 전라남도 남부해역), 서해(목포-인천, 254-356)이다. 제주해역은 생태구역과 동일하다.
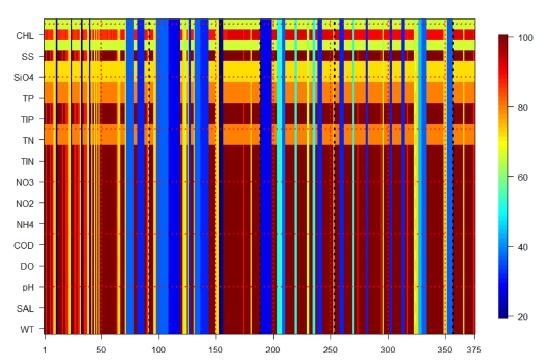
통계정보 계산 과정에서 변동 범위가 크게 나타나는(관측 수치가 1, 10, 100 정도의 변동을 보이는) 영양염류(nutrients), SS, chlorophyll-a 항목은 로그변환 자료를 이용하였다. 전체 정점은 정점의 위치에 따라 그룹으로 통합하고, 각각의 그룹에서 관측정점의 개수를 정렬하여 제시하였다(Table 1 참조, 논문 그림에서 사용하는 정점번호는 누적번호와 동일). 그리고 관측정점의 가용한 자료개수를 항목별로 추정하여 KOEM 모니터링 모든 정점, 모든 항목의 자료 가용 수준(자료 개수, 결측 양상)을 파악할 수 있도록 행렬을 구성하여 이미지 도시(image plot)로 제시한다(Fig. 1 참조). 1997년부터 현재 까지 운영-유지되는 정점의 경우, 빠짐없는 관측을 수행한 경우, 자료의 개수는 모두 100개(=25년×4개/연)가 된다. 그보다 작은 자료개수는 1997년 이후의 신규 (추가) 정점 또는 관측항목의 결측(missing) 영향이다. 본 연구에서는 모든 정점에서 결측이 없는 2017-2021년 기간의 자료 조건에서 수행을 하였기 때문에 가용 자료의 개수가 매년 4개(총 5년 동안 20개)로 일정하지만, 분석기간을 확장하는 경우, 정점에 따른 가용자료 개수의 영향 및 관측항목 개수의 영향을 고려할 필요가 있다.
2.2 분석 방법 및 분석 범위
해양환경측정망 자료는 관측정점, 항목, 시기가 모두 다른 다지점(multi-station), 다항목(multi-variate), 다년간(multi-year)의 독립적인 자료세트로 간주할 수 있으며, 매우 다양한 분석 조합이 가능하다. 최근 2021년 자료로 구성되는 관측시점을 통합한 독립적인 자료세트는 정점(375)×관측항목(31)=11,625개 정도로 가능한 분석조합 개수는 관측항목의 통합 분석(항목평균의 제약)보다는 정점통합 분석이 요구되는 상황이다. 이 모든 조합에 대한 다양한 통계적인 추정, 검정 등은 가능하다 할지라도 그 모든 조합을 분석하는 것은 실질적으로 불가능하다. 따라서 본 연구-분석에서는 다음 조합을 기준으로 분석 범위를 제한하였다. 분석 조합은 다양한 기준에 따라 다양한 선택이 가능하지만, 분석 조합을 관심 영역(분야), 분석 목표 등으로 제한하는 것은 불가피한 선택이다. 다양한 분석조합을 선택하는 경우에는, 간단한 분석이라 할지라도 그 분석내용이 방대해지기 때문에 ‘수박겉핥기’수준의 분석이 될 수 있다. 따라서 본 연구에서는 분석항목을 수질평가등급 WQI 계산에 이용되는 Secchi depth(투명도, m), 표층 TIN(총용존무기질소, mg/L), 표층 TIP(총용존무기인, mg/L), 표층 엽록소(chlorophyll-a, μg/L), 저층/표층 용존산소(DO, mg/L) 항목으로 제한하였다. 또한, 관측시기에 따라 관측정점의 개수가 증가하는 변화영향을 회피하기 위하여 관측정점이 고정된 최근 5년 자료(2017년-2021년)로 분석 기간을 제한하고, 관측 정점에 대한 평균과 표준편차의 신뢰구간 변화 양상에 중점을 두고 분석을 수행하였다. 자료의 분석 목적에 따라 적절한 분석 방법과 범위를 조정할 필요가 있다. 본 연구에서는 평균의 오차구간 분석을 가장 기본적인 분석으로 간주한다. 또한 평균 오차분석에 필요한 분산과 표준편차에서도 표준편차 항목을 선택한이유는 “평균과 표준편차는 관측항목의 단위와 동일하다”는 장점에 기인한다.
표본자료의 평균과 표준편차 신뢰구간 추정 공식은 통계 교과서에 제시되는 가장 기본적이고도 중요한 공식이다. 하나의 관측정점, 관측항목의 경우 자료의 개수가 1년에 4개이며, 전체 5년 자료를 모두 통합하는 경우에도 20개 정도로 소표본(small samples)에 해당한다. 본 연구에서는 아래 제시되는 공식을 이용하여 모든 관측 정점에서, 주요 6개 수질항목을 대상으로 매년(2017년-2021년, 5년) 평균과 표준편차의 신뢰구간을 추정하였다.
평균의 신뢰구간 공식은 다음과 같다(Agresti & Franklin[2007]; Sokal & Rohlf[1987]; Sung[2004]; Kim et al.[2000]).
| (1) |
| (2) |
여기서, n = 자료의 개수, = 표본의 평균, sX= 표본의 표준편차, μ = 추정하고자 하는 모집단(population)의 평균, σX = 모집단의 표준편차, α = 유의수준(significance level, 본 연구의 경우, α = 0.05, 신뢰구간 = 1−α)이다. 한편, t(df, p)= 자유도(df, degree of freedom = n−1)와 유의수준으로 부여되는 상한-하한 확률(p, probability, α/2, 1−α/2, α, 1−α) 조건에서 계산되는 Student t-분포 계수이다.
관측 자료를 이용하여 모평균을 추정하는 과정에서, 모집단의 표준편차를 모르는 경우가 일반적이기 때문에, 모집단의 표준편차는 표본의 표준편차를 이용한다. 표본평균의 신뢰구간은 대칭으로, 평균 기준 절대적인 차이로 신뢰구간의 크기가 결정되기 때문에, 평균이 다른 관측정점의 신뢰구간 크기 비교에는 부적절하다. 따라서 본 연구에서는 신뢰구간을 평균으로 나눈 정규화된 신뢰구간(normalized CI) 정보를 제안한다. 이 경우, 표본평균의 신뢰구간은 1.0 수치를 기준으로 상하(±) 동일한 크기를 가진 구간이 되고, 평균 크기로 정규화 하였기 때문에 절대적인 크기가 아닌, 상대적인 비율로 표현된다. 절대적인 크기평가, 상대적인 비율 평가의 선택은 수질항목의 특성과 어떤 수치의 이해 수월 정도에 따라 결정한다.
표본의 표준편차, 분산도 다음과 같이 신뢰구간이 계산된다. 표준편차의 신뢰구간도 관측정점에 따라 표준편차가 차이를 보이기 때문에, 평균과 마찬가지로 비율 비교를 위한 표준편차의 정규화된 신뢰구간을 다음과 같이 제안한다. 이 경우, 표준편차의 신뢰구간 비율은 1.0 수치를 기준으로 모든 지점에서 동일한 상한-하한 비율을 가지게 된다. 상한 비율은 1.0 보다 크고, 하한비율은 1.0 보다 작은 수치로 제시된다(Otto & Longnecker[2001]; Sokal & Rohlf[1987]).
| (3) |
| (4) |
3. 결과 및 고찰
3.1 평균과 표준편차의 변동양상
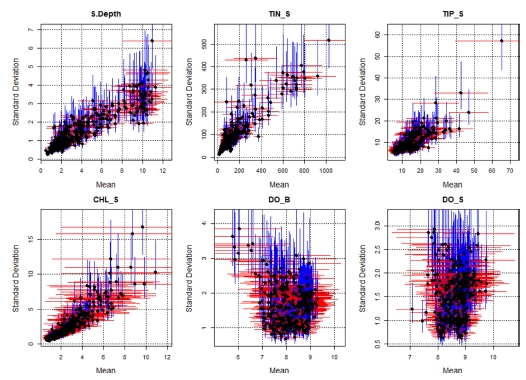
모든 관측정점, 모든(=5년) 관측기간의 자료(자료개수=20)를 이용하여 계산한 평균과 표준편차의 신뢰구간은 다음과 같다. 추정된 평균과 표준편차, 그리고 각각의 신뢰구간을 산포도로 모든 항목에 대하여 도시한 그림은 다음과 같다(Fig. 2 참조). 그림에서 볼 수 있는 바와 같이 하나의 큰 영역에 집중되는 DO 항목의 평균, 표준편차 변화 양상과는 달리, 다른 모든 항목은 평균의 증가에 따라 표준편차도 증가하는 뚜렷한 양상을 보이고 있으며, 신뢰구간의 크기도 비례하여 증가하는 양상을 보이고 있음을 알 수 있다. 전체적인 자료가 집중된 영역에서 크게 벗어나는 영역은 이상 자료(outliers, 유난히 농도가 높은 해역의 자료)로 간주할 수 있다. 그러나 이상 자료가 전체 자료개수에서 차지하는 비율은 낮아도 높은 수치로 인하여 전통적인 통계측도 추정에 큰 영향을 미칠 수 있기 때문에, 이상 자료 진단기법을 이용하여 분석 대상에서 제외하거나 로버스트(robust) 추정방법의 도입 등이 요구된다. 우리나라 해역 전체 자료의 분석은 특정 구간의 높은 항목보다는 발생 빈도의 관점에서 평균적인 수치분석이 필요하다. 본 연구에서도 이상 자료 보다는 전체적인 자료의 평균에 중점을 두고 분석을 수행하였다.
3.2 평균의 신뢰구간 변화 양상
대표 6개 수질 항목을 대상으로, 모든 정점에 대하여 평균과 표준편차 항목에 대하여 95% 신뢰구간을 5년간의 자료를 이용하여 추정하였다. 아래 그림은 저층 DO 항목에 대한 2021년 평균과 신뢰구간을 정점별로 표시한 그림이다(Fig. 3 참조). 그림에서 볼 수 있는 바와 같이, 관측 정점에 따라 평균 변화와 신뢰구간의 크기변화가 상당한 차이를 보이고 알 수 있다. 신뢰구간의 변화 크기를 비교하기 위하여 최근 5년간의 자료를 모두 이용하여 평균의 신뢰구간을 추정한 결과도 그림으로 제시하였다(Fig. 4 참조, 그림의 지점분할 구간은 해역구분, 동해, 남해동부, 남해서부, 서해, 제주해역). 동일한 크기 수준에서의 비교를 위하여 농도크기를 나타내는 세로축의 범위를 일정한 범위(0-20 mg/L)로 고정하였다. 그림에서도 뚜렷하게 드러나는 바와 같이, 자료 개수(관측빈도)의 증가로 인한 신뢰구간 감소(신뢰구간의 크기를 의미하는 연직방향 적색 막대의 길이가 Fig. 3 조건에 비하여 Fig. 4 조건에서 크게 감소)가 뚜렷하게 나타나고 있음을 알 수 있다. 관측 자료의 평균, 표준편차 등은 연도, 계절에 따라 다를 수 있지만, 자료의 개수가 작은 경우에는 추정 평균과 표준편차의 신뢰구간은 자료의 개수가 가장 우세한 인자에 해당된다.
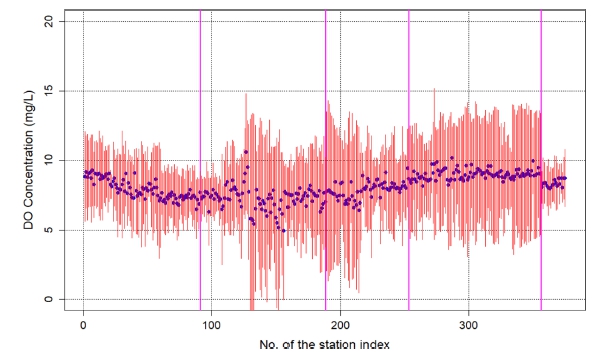
Variation pattern of the mean and confidence intervals of the bottom DO concentrations at all monitoring stations (2021).
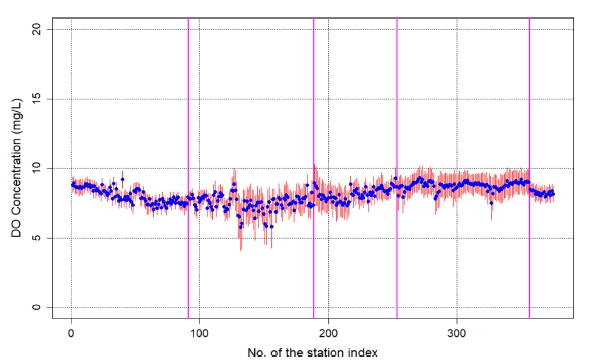
Variation pattern of the mean and confidence intervals of the bottom DO concentrations at all monitoring stations (5-years data).
관측빈도의 증가 또는 구간추정에 사용하는 자료 개수의 증가효과는 표준편차와 자료의 개수로 결정되기 때문에 적절한 허용 가능한 오차(신뢰구간의 크기)를 결정(선택)할 경우, 요구되는 자료의 개수를 결정할 수 있다(Fig. 5 참조). 허용오차를 만족하기 위하여 필요한 자료의 개수는 대상 수질항목의 표준편차가 영향을 미치기 때문에 수질항목에 따라 차이를 보이게 된다. 그림에서 보이는 평균 CI 범위의 상한, 하한과 표준편차 비율 상한, 하한은 각각 다음과 같은 자료 개수(n), 유의수준(α = 0.05)의 함수로 표현된다.
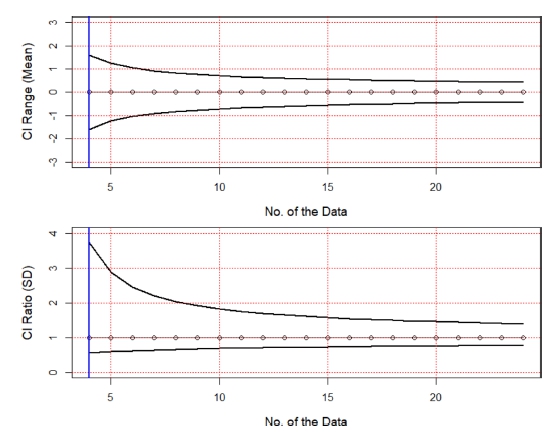
Confidence interval coefficients variation for the number of the data (normalized CI for the mean and CI ratio for the SD).
Upper and lower limits of the mean CI range:
Upper and lower limits of the SD CI ratio:
여기서, t(df,α), = 각각 Student-t 분포함수, X2(chi-square) 분포함수의 자유도(df = n−1), 유의수준(α)에 해당하는 통계변량으로, 입력 정보는 유의수준, 신뢰수준으로 주어지는 0-1 범위의 확률이다.
매년 자료를 이용하여 추정한 평균과 신뢰구간의 구간추정 수치정보는 아래에 표로 정리하여 제시한다(Table 2 참조). 로그 변환으로 추정한 TIN, TIP, 엽록소 농도 항목은 변환조건에서 추정한 신뢰구간을 관측 농도에 해당하는 수치로 다시 환산한 결과이며, Secchi depth, 표층-저층 DO 농도 항목은 변환 없이 추정한 결과이다.
3.3 최적 관측빈도
최적 관측빈도에 대한 고찰에 앞서 바람직한 관측 빈도는 무엇인가? 과학적인 측면에서의 요구되는 “바람직한” 관측빈도는 분석목표에 부합되는 추정이 가능한 관측빈도를 의미하며, 분석목표에 부합되는 최적 관측빈도는 허용 가능한(acceptable, tolerable) 오차 크기 조건(제약)을 만족하는 최소 자료의 개수를 의미한다. 허용 가능한 오차의 기술적인(descriptive) 정의는 가능하지만, 허용 가능한 오차는 항목, 기술수준, 관측 빈도 및 지점의 개수, 그리고 표본 자료에 해당하는 관측 자료를 이용하여 추정하고자 하는 통계측도의 추정 오차, 연구 분야의 분석 수준 등 매우 다양한 인자의 영향을 받는다. 또한 이론적으로, 과학적으로 유도되는 기준이 없기 때문에 허용 가능한 오차는 고정된 과학적인 기준보다는 기술 수준과 관측환경을 고려한 경험적인 기준 설정이 요구되는 상황이다. 최적 관측 빈도도 과학적인 분석 수준과 더불어 현장에서의 현실적인 관측 빈도를 고려하여 설정하는 것이 적절하다. 목표 허용 기준을 현재의 관측 자료를 이용한 추정으로 만족 못 하는 경우에는, 현재의 오차 구간의 크기를 받아들이는 것이 불가피하다.
한편, 어느 정도의 범위에서 선정 또는 지정된 “허용 가능한” 오차조건에서 기존 관측 자료의 평균과 표준편차 정보를 이용하면 그 조건을 만족하는 최소 자료개수 추정이 가능하다. 따라서 최적 관측오차는 허용 가능한 오차, 목표 오차 선정이 선행되어야 한다. 본 연구에서는 임의의 크기(비율) 범위를 허용 가능한 오차로 선정하고, 평균과 표준편차의 신뢰구간 추정 공식을 이용하여 최소 자료개수를 산정하였다. 추정에 사용되는 수식은 다음과 같다.
○ Normalized 평균(μ/)의 허용오차 구간.
○ 표준편차 비율(σX/sX)의 허용오차 구간.
평균의 허용오차구간을 평균 대비 비율 ±10% 수준(0.9-1.1)으로 설정하는 경우, 저층 DO 항목의 경우, 20개 이상, 표층 DO 항목의 경우에는 14개 이상이 요구된다. 항목에 따라 평균과 표준편차 정보가 다르기 때문에 하나의 고정된 기준을 사용하기에는 한계가 있으나, 저층 DO 항목을 기준으로 하는 경우에는 20개 이상 조건을 만족하여야 하며, 현재의 관측빈도 조건에서 이 조건을 만족하기 위해서는 최근 5년간의 자료를 이용하여 평균을 추정하야야 함을 의미한다. 연4회 관측조건에서 얻어진 자료를 이용하여 매년 평균을 비교하는 과정은 통계적으로는 무의미한 검정 결과를 얻게 된다.
한편, 표준편차의 비율에 대한 상한-하한 크기는 자료의 개수로 결정된다. 상한표준편차의 비율이 2.0배(2.0) 이하 조건을 만족하기 위해서는 표본의 개수는 9개 이상, 1.5배(1.5) 이하 조건을 만족하기 위해서는 18개 이상 조건이 요구된다. 하한 표준편차의 비율은 70%(0.7) 이상 조건을 만족하기 위해서는 12개 이상, 80%(0.8) 이상 조건을 만족하기 위해서는 32개 이상으로 판단되었다.
이상의 허용 가능한 오차 기준으로 필요한 추정한 자료의 개수는 실질적으로 현장에서 확보하기 어려운 조건에 해당할 수도 있다. 그러나 현장에서의 어려운 여건, 또는 한정된 예산/인력조건에서 수행되는 현재의 관측빈도 조건으로는 본 연구에서 추정한 주요 매개변수의 신뢰구간(불확실성의 크기)에 대한 고려가 필요하다. 현재 수준에서 받아들여야만 하는 (발생 가능한) 오차구간의 크기이기 때문에, 보다 적절한 정책수립/효과분석에 활용하기 위해서는 가용한 자료의 통합을 통하여 통계정보를 추정하는 과정이 필요하다. 추정을 위한 자료의 기간은 항목별로 차이를 보이고 있으나 최소 3-5년 정도가 적절한 수준으로 판단된다.
4. 결 론
해양환경측정망 자료를 이용하여 DO, 표층 TIN, 표층 TIP, Secchi Depth(m), 엽록소 농도(chlorophyll-a) 항목의 평균과 표준 편차의 신뢰구간 추정-분석을 수행하였다. 모든 정점에서의 95% 신뢰구간의 크기 분석 결과를 기반으로 다음과 같은 결론을 도출하였다.
(1) 현재 수행되는 연4회 관측 자료를 이용한 평균 추정오차는 항목에 따라 차이를 보이지만, 저층 DO 항목 평균 대비 비율이 ±33% 정도를 크게 벗어나는 수준으로 다양한 환경관리 정책수립 및 대책평가에 부적절한 수준으로 판단된다.
(2) 통계적인 추정 결과에 대한 절대적인 허용 가능한 오차는 설정되어있지 않으나, 일반적인 ±10% 정도의 허용오차 비율 조건을 적용하는 경우, 최소 3-5년 정도의 관측 자료를 이용한 평균, 표준 편차 추정이 요구된다.
(3) 현재 연안 해역에서의 환경인자 관측은 비용과 인력의 제한으로 연4회 수행하고 있으나, 매년 추정되는 평균, 표준편차의 오차 절감을 위해서는 해역을 대표하는 기준 정점을 선택하여 연간 6-12회 정도로 관측 빈도를 조정할 필요가 있다. 그러나 실질적으로 해양에서의 관측빈도 증가는 큰 어려움이 예상되기 때문에 인접한 연도의 자료를 이용하여 평균 추정에 사용되는 자료의 개수를 늘리는 방법이 적절한 방법으로 판단된다.
Acknowledgments
본 연구는 독도의 지속가능한 이용연구(PG-53502) 사업의 지원을 받아 수행되었습니다. 또한 본 연구에서 사용한 관측 자료를 제공해 준 KOEM(해양환경공단)에 감사를 드립니다.
References
- Agresti, A. and Franklin, C., 2007, Statistics, The Art and Science of Learning from Data, Chapter 7, Pearson Prentice Hall, New Jersey.
-
Jeong, J.H., Lim, J.H., Kim, G.Y., Rho, T.K., Lee, Y.W. and Tac, D.H., 2018, A Study on Revision of Water Quality Index for Seawater, J. Korean Soc. Mar. Environ. Energy, 21(4), 293-305.
[https://doi.org/10.7846/JKOSMEE.2018.21.4.293]

-
Kim, D.S., Choi, H.W., Kim, K.H., Jeong, J.H., Baek, S.H. and Kim, Y.O., 2011, Statistical Analysis on the Quality of Surface Water in Jinhae Bay during Winter and Spring, Ocean and Polar Research, 33(3), 291-301.
[https://doi.org/10.4217/OPR.2011.33.3.291]

- Kim, U.C., Kim, J.J., Park, B.W., Park, S.H., Park, T.S., Song, M.S., Lee, S.Y., Lee, Y.J., Jun, J.W. and Cho, S.S., 2000, Introduction to Statistics, The Fourth Edition, Youngji.
-
Kim, Y.S., Lee, Y.H. and Choi, H.G., 2012, Water Quality Assessment at Coastal Area of the East Sea of Korea, J. of Korean Society of Marine Environment and Safety, 18(1), 15-24.
[https://doi.org/10.7837/kosomes.2012.18.1.015]

- Kwon, J.N., 2010, Characteristic of Long term Variation of the water Quality at the Waters of Goseong Bay, J. of the Korean Society for Marine Environmental Engineering, 13(4), 279-287.
-
Kwon, J.N., Lim, J.H., Shim, J.H., Lee, J.H. and Choi, T.J., 2014, The Long-Term Variations of Water Quality in Masan bay, South Sea of Korea, J. of the Korean Society for Marine Environment and Energy, 17(3), 212-223.
[https://doi.org/10.7846/JKOSMEE.2014.17.3.212]

-
Kwon, J.N., Park, Y.C. and Eom, K.H., 2013, The Characteristic of Long Term Variation of the Water Quality from Hansan-Geoje Bay, Korea, J. of the Korean Society for Marine Environment and Energy, 16(3), 189-201.
[https://doi.org/10.7846/JKOSMEE.2013.16.3.189]

- Lee, I.C. and Oh, Y.J., 2006, Spatio-temporal change of Water Quality in Jinhae Bay, Korea, Proc. of the KOSMEE Fall Meeting, 84-89.
- Marine Environmental Information System, 2022. https://www.meis.go.kr/portal/ (Accessed 2022.09.05.)
-
Nam, H.J., Heo, S., Park, S.Y., Hwang, U.K., Park, J.S. and Lee, H.K., 2012, The Physico-Chemical Characteristics in the Garorim Bay, Korea, J. of Korean Society of Marine Environment and Safety, 18(2), 101-114.
[https://doi.org/10.7837/kosomes.2012.18.2.101]

- Ott, R.L. and Longnecker, M., 2001, An Introduction to Statistical Methods and Data Analysis, Fifth Edition, Chapter 7, Duxbury.
-
Park, M.O., Lee, Y.W., Park, J.K., Kang, C.S., Kim, S.G., Kim, S.S. and Lee, S.M., 2019, Evaluation of the Seawater Quality in the Coastal Area of Korea in 2013-2017, J. Korean Soc. Mar. Environ. Energy, 22(1), 47-56.
[https://doi.org/10.7846/JKOSMEE.2019.22.1.47]

- Park, S.J. and Shin, Y.S., 2022, Characteristics of Water Quality and Chlorophyll-a in the Seawater Zone of the Youngsan River Estuary: Long-term (2009-2018) Data Analysis, Ocean and Polar Research, 44(1), 13-27.
- Sokal, R.R. and Rohlf, F.J. 1987, Introduction to Biostatistics, Second Edition, Chapter 6, Dover Publications, New York.
- Sung, T.J., 2004, Understanding and Application of the Modern Fundamental Statistics, Revised Edition, Education & Science Co.