기계학습 기법과 해색 위성 자료를 이용한 실시간 저층 용존산소농도 산출기술 개발 연구
초록
본 연구에서는 해색 위성 자료와 해양환경측정망 자료를 활용하여 시공간적 고해상도의 연안 저층 용존산소(dissolved oxygen, DO) 농도 산출을 위한 기계학습 모델을 개발하였다. 저층 DO 농도 산출을 위한 최적 모델로는 Gaussian process regression이 선별되었으며, 최적 예측변수로는 해색 위성 자료 중[원격반사도 6종, chlorophyll a 농도, 입자태 유기 탄소 농도, 분산광 소산 계수, 해수면 온도]가 선별되었다. 최적 예측변수 및 모델로 빈산소수괴가 가장 빈번하게 발생했던 대한해협의 저층 DO 농도를 산출했으며, 그 산출치와 관측치 간의 결정계수(R2)와 평균제곱오차(MSE)는 각각 0.69, 1.23으로 나타났다. 이후, 모델 정확도 개선 과정을 거친 최종 모델의 R2와 MSE는 각각 0.83, 0.47로 정확도 개선 전 대비 20.3, 61.8% 개선된 결과를 보였다. 매년 여름철 빈산소수괴로 어업 피해가 발생하고 있는 현재, 본 기술은 실시간 빈산소수괴 발생 탐지를 위한 기초 기술로 활용될 수 있을 것이다.
Abstract
In this study, we developed machine learning-based models for the spatiotemporal high-resolution estimation of coastal bottom dissolved oxygen (DO) concentration using ocean color data and marine environmental monitoring system data. Gaussian process regression was selected as the optimal model for bottom DO concentration estimation, and the optimal predictor variables were chosen as six types of remote sensing reflectance, chlorophyll-a, particulate organic carbon concentration, diffuse attenuation coefficient, and sea surface temperature. Utilizing the optimal predictor variables and model, we estimated the bottom DO concentration in the South Sea of Korea, which is prone to frequent hypoxia events. The coefficient of determination (R2) and mean squared error (MSE) between the estimated and observed values were 0.69 and 1.23, respectively. Subsequently, after a process of model accuracy improvement, the R2 and MSE of the final model were enhanced to 0.83 and 0.47, indicating a 20.3% and 61.8% improvement, respectively, compared to the accuracy before improvement. Given the recurring hypoxia events causing damage to fisheries, the current technology could be employed as a fundamental tool for real-time detection of hypoxia water mass, offering a promising solution.
Keywords:
Hypoxia Water Mass, Gaussian Process Regression, Communication, Ocean and Meteorological Satellite, Marine Environmental Monitoring System키워드:
빈산소수괴, 가우시안 과정 회귀, 천리안 위성, 해양환경측정망1. 서 론
용존산소(dissolved oxygen, DO) 농도가 3 mg L-1 이하인 수괴를 빈산소수괴(hypoxia water mass)라 한다. 3.6 mg L-1 이하의 DO 농도에서 저서동물의 폐사가 시작되며, 3 mg L-1 농도의 DO는 해양 생물의 최저 인내 한계로 작용한다. 해역의 DO가 고갈되면 생물이 더 이상 살 수 없는 Dead zone이 형성되어 해양생물자원은 감소하게 된다(Breitburg et al.[2018]; Yin et al.[2004]). 빈산소수괴의 발생 빈도, 강도, 그리고 지속시간은 전 세계적으로 증가하고 있는 추세이다(Chan et al.[2008]; Stramma et al.[2008]). 빈산소수괴가 장기간 형성될 경우 저서 생태계는 황폐해지며, 그 결과 Dead zone이 형성될 수 있다(Conley et al.[2007]). 빈산소수괴와 그로 인한 Dead zone은 주로 연안역에서 발생한다. 연안으로 유입되는 육지 기원의 고농도 영양염은 식물플랑크톤의 대량 증식을 야기하며, 그것의 호흡과 사후 분해를 위한 산소 소모는 빈산소수괴의 주된 원인 중 하나이다(Howarth et al.[2011]). 육지 기원의 다량의 유기물질은 저층으로 퇴적되어 분해되는데 산소를 소비하는데, 특히 빈산소 조건에서 발생하는 유기물질의 분해는 H2S와 같은 독성물질을 발생시킨다. 연안 생태계의 보존과 수산 자원의 지속 가능한 이용을 위해 빈산소수괴의 모니터링과 그 대응은 매우 중요하다.
50% 치사시간(median lethal time, LT50)은 특정 조건에서 생물집단의 50%가 사멸되는데 걸리는 시간을 의미한다(Duffus[1993]). 해양 생물 206개 종의 빈산소수괴에 대한 LT50을 조사한 연구 결과, 그 하위 10% 값은 6.8 시간에 불과했다(Vaquer-Sunyer and Duarte[2008]). 연안 생태계 보호를 위해서는 저층 DO 농도에 대한 시공간적 고해상도의 모니터링이 필요한 상황이지만, 국내에는 아직 이에 대한 시스템이 없다. 국내에서 운영 중인 연안 저층 DO 농도 모니터링은 해양환경공단의 해양환경측정망과 해양수질자동측정망, 그리고 국립수산과학원의 어장환경모니터링이 있다. 하지만, 해양환경측정망과 어장환경모니터링은 2~3개월 간격 자료로 실시간 모니터링이 불가하며, 해양수질자동측정망은 그 정점 수가 적고 위치가 하구역에 한정되어 공간적 해상도가 낮다.
시공간적 고해상도의 빈산소수괴 발생 탐지를 위한 방법으로는 해색 위성 자료를 활용한 저층 DO 농도 산출이 있다. Kim et al.[2020]은 MODIS와 VIIRS의 해색 위성 자료와 다중회귀분석을 사용하여 서해안의 DO 농도를 높은 정확도로 산출할 수 있었다. 하지만, 이 연구는 빈산소수괴 발생 빈도가 적은 서해안을 대상으로 하고 있으며, 특히 빈산소수괴가 발생하는 저층이 아닌 표층 DO 농도를 산출하였다. 이 외에도 관련 연구가 수 차례 수행되었으나, 대부분 정적인 연못이나 호수 또는 표층 DO 농도만을 대상으로 하고 있다(Guo et al.[2021]; Shao et al.[2023]). 또한, 연구에 사용된 글로벌 위성 자료들은 이동궤도 위성 특성상 시공간적 해상도가 정지궤도 위성에 비해 낮다. 국내에서 운영 중인 천리안 위성은 세계 최초의 정지궤도 해양 관측 위성으로 그 시공간적 해상도가 1시간·500 m로 매우 높다. 천리안 위성의 해색 자료와 기계학습 기법의 활용은 기존의 방법보다 높은 정확도와 시공간적 해상도로 저층 DO 농도를 산출할 수 있을 것이며, 이는 실시간 빈산소수괴 탐지를 위한 기초자료로 활용될 수 있을 것이다.
본 연구에서는 해양환경측정망의 DO 농도 자료와 천리안 위성의 해색 자료를 사용하여 국내 연안의 실시간 저층 DO 농도 산출 모델을 개발하였다. 먼저, 네 종류의 기계학습 모델별 성능 평가를 통해 최적 모델을 선별하였다. 이후, 정확도 개선 과정을 거쳐 최종 모델을 개발하였다.
2. 재료 및 방법
2.1 해양환경측정망 관측 자료
생태구별·분기별 빈산소수괴 발생 빈도 분석과 저층 DO 농도 산출 모델 개발을 위해 해양환경공단에서 제공하는 해양환경측정망의 DO 농도가 사용되었다(KOEM[2023]). 해양환경측정망 정점은 총 425개로 국내 5개 연안 생태구[대한해협(South sea, SS), 동해(East sea, ES), 서남해역(West-south sea, WSS), 서해중부(West-middle sea, WMS), 제주(Jeju, JJ)]의 분기별 표층과 저층에서 관측된 해수 일반항목 16가지를 제공한다. 본 연구에서는 2012년 2월 ~ 2021년 2월 자료 중 결측치와 이상치를 제외하고 총 14,004개의 DO 농도 자료가 사용되었다.
2.2 해색 위성 자료
기계학습 기반의 저층 DO 농도 산출을 위한 예측변수로 해색 위성 자료를 사용하였다. 예측변수로는 천리안 위성의 원격반사도 6종(Rrs412, Rrs443, Rrs490, Rrs555, Rrs660, Rrs680), chlorophyll a(Chl.a) 농도, 입자태 유기 탄소(particulate organic carbon, POC) 농도, 분산광 소산 계수(diffuse attenuation coefficient, DAC), 그리고 Aqua-MODIS 위성의 해수면 온도(sea surface temperature, SST)가 사용되었다(NOAA[2023]). 천리안 위성 자료는 1시간, 500 m의 시공간 해상도로 제공되며, 본 연구에서는 일별 평균하였다. Aqua-MODIS의 SST는 1일, 4 km의 시공간 해상도로 제공되며, 천리안 위성 자료의 위경도 좌표상에 보간·맵핑하였다. 맵핑된 두 해색 위성 자료는 해양환경측정망의 DO 농도 정점에 다시 맵핑하였으며, 위성 자료 결측치를 제외하고 총 3,096개의 관측 자료가 사용되었다. 예측변수와 저층 DO 농도의 기본 통계량은 Table 1에 나타내었다.
2.3 저층 DO 농도 산출을 위한 기계학습 모델 개발
저층 DO 농도 산출을 위한 예측변수로 해색 위성 자료 10종(Rrs 6종, Chl.a, POC, DAC, SST)이 사용되었다. 모델 학습 전 예측변수 평가를 위해 반응변수인 저층 DO 농도와 각 예측변수 간의 1) 선형회귀 t-test의 p-value 및 2) random forest 기반의 feature importance를 계산하였다. 선형 회귀의 t-test는 예측변수를 선별하는 방법의 하나로 ‘독립변수의 계수(또는 가중치)는 0이다’라는 귀무가설 검정을 진행한다. 검정 결과 그 확률(p-value)이 0.05 이하일 경우 가설은 기각되며 해당 항목은 예측변수로서 유의하다. random forest 기반의 feature importance는 그 값이 클수록 변수의 중요성이 크다는 것을 의미한다.
전체 자료 중 2,477개(80%)는 자료의 평균과 표준편차를 각각 0과 1로 만드는 표준화(Standardization) 과정을 거친 후 모델 학습에 사용되었으며, 나머지 619개(20%)는 모델 검증에 사용되었다. 모델 후보로는 기계학습 기반의 Decision tree, Support vector machine, Neural network, Gaussian process regression(GPR)이 고려되었다. 각 모델의 hyperparameter는 베이지안 최적화를 바탕으로 최적화되었다. DO 농도 산출치와 관측치 간의 목적함수 값으로부터 모델 후보들을 평가하였으며, 평가 결과를 바탕으로 최적 모델을 선별하였다. 모델 평가를 위한 목적함수로는 결정계수(R2), 평균 제곱근 오차(RMSE), 평균 제곱 오차(MSE), 평균 절대 오차(MAE)가 사용되었다.
| (1) |
| (2) |
| (3) |
| (4) |
모델 후보 중 Decision tree는 분류 및 회귀 문제에 사용되는 지도 학습 알고리즘이다. 데이터를 재귀적으로 분할하여 트리 구조를 형성하며, 직관적이고 해석이 쉽다는 장점이 있다. 복잡한 자료보다는 단순한 자료 예측에 적합하다(Charbuty and Abdulazeez[2021]). Support vector machine은 선형과 비선형 문제에 적용 가능한 지도 학습 알고리즘이다. 주어진 자료를 고차원 공간으로 맵핑하여 최적의 결정 경계를 찾을 수 있기 때문에 회귀보다는 분류 문제에 적합한 모델로 평가받는다(Zhang[2012]). Neural Network은 신경망 모델로 인공 뉴런들을 계층적으로 구성하여 복잡한 문제를 모델링 할 수 있다. 대규모 데이터셋에 뛰어난 성능을 보이나, 모델의 과적합(Overfitting) 문제가 자주 발생하며, 훈련 시간과 계산 비용이 크다는 단점이 있다(Lawrence et al.[1997]). 마지막으로 GPR은 기계학습-커널(kernel) 함수 기반의 non-parametric 모델로 입력자료의 분포를 고려하여 함수의 확률적인 분포를 추론한다. GPR은 학습자료에 대해 높은 유연성을 가지며, 해양의 DO 농도와 같은 복잡한 자료 예측에 적합하다(Park et al.[2021]).
선별된 최적 모델은 정확도 개선을 위해 다음 세 가지 과정을 순서대로 거쳤다. 1) 최적 예측변수 선별: 예측변수 평가 결과를 바탕으로 최적의 예측변수 조합 선별, 2) 예측변수 생성: 표층 DO 농도를 산출하여 이를 다시 저층 DO 농도 산출을 위한 예측변수로 사용, 3) 생태구별 모델 분리: 자료를 생태구별로 나눠 각각 모델 학습.
‘최적 예측변수 선별’을 위해 선형회귀 t-test의 p-value와 feature importance 값을 기준으로 네 가지 조합의 예측변수 후보가 고려되었다. 예측변수 후보 선별 기준은 다음과 같다. 1) t-test의 p-value가 0.05 이하, 2) feature importance가 1.5 이상, 3) p-value가 0.05 이하이면서 feature importance가 1.5 이상, 4) 모든 변수. 예측변수 후보별 최적 모델을 학습하여 그 목적함수 값으로부터 최적 예측변수를 선별하였다. 선별된 최적 예측변수로 학습된 모델을 Model-UP1으로 정의하였다.
‘예측변수 생성’에서는 최적 모델과 예측변수를 이용하여 표층 DO 농도를 산출하였으며, 이를 다시 기존 예측변수들과 함께 예측변수로 사용하여 저층 DO 농도를 산출하였다. 이 기법은 우리의 이전 연구에서 모델 성능을 약 10% 개선하는 결과를 보였었다(Park and Kim[2023]). ‘최적 예측변수 선별’과 ‘예측변수 생성’ 기법이 적용된 모델을 Model-UP2로 정의하였다.
최적 예측변수 선별과 예측변수 생성 이후 ‘생태구별 모델 분리’ 과정을 거쳐 최종 모델을 개발하여 Model-UP3로 정의하였다. ‘생태구별 모델 분리’를 위해 자료를 5개의 생태구(대한해협, 동해, 서남해역, 서해중부, 제주)별로 나눠 각각 모델을 학습하였다.
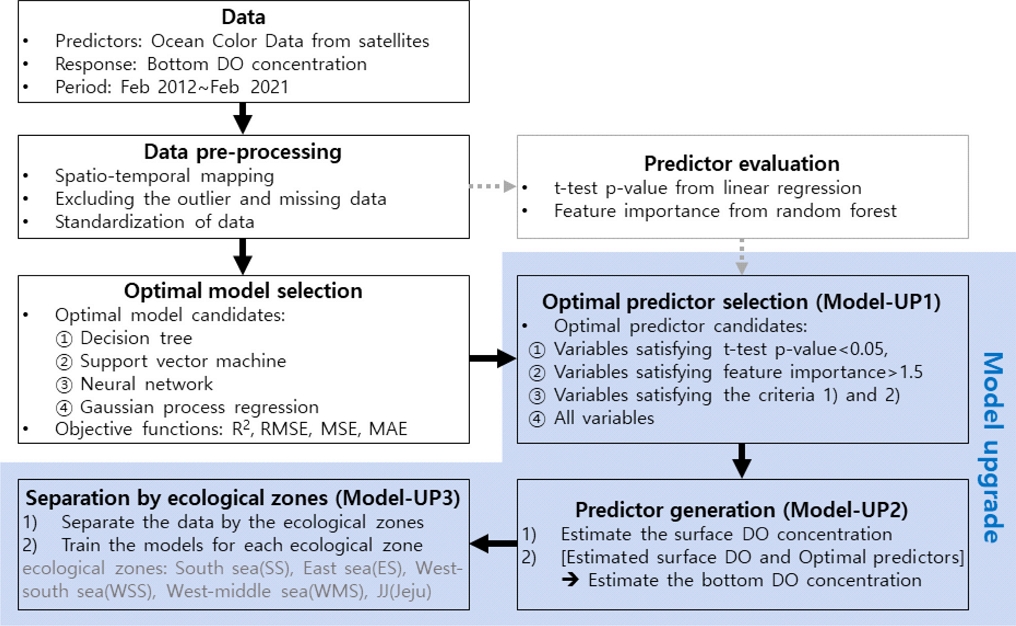
해색 위성 자료와 기계학습을 활용한 실시간 저층 DO 농도 산출 모델의 개발 순서도를 Fig. 1에 나타내었다.
3. 결과 및 고찰
3.1 해양환경측정망 정점의 분기별 빈산소수괴 발생 현황
2012년 2월부터 2021년 2월까지 분기별 관측된 해양환경측정망의 저층 DO 농도를 바탕으로 통계한 생태구별 빈산소수괴 발생 정점과 분기별 총 발생 빈도를 Fig. 2에 나타내었다. 대한해협의 180개 정점 중 38개의 정점에서 빈산소수괴가 발생했으며, 그중 26개 정점은 진해만 내에 위치하고 있다. 서남해역에서는 56개 정점 중 2개의 정점에서 빈산소수괴가 발생했으며, 서해중부에서는 86개 정점 중 1개의 정점에서 발생하였다. 동해 77개 정점과 제주 26개 정점에서는 관측 기간 동안 빈산소수괴가 관측되지 않았다.
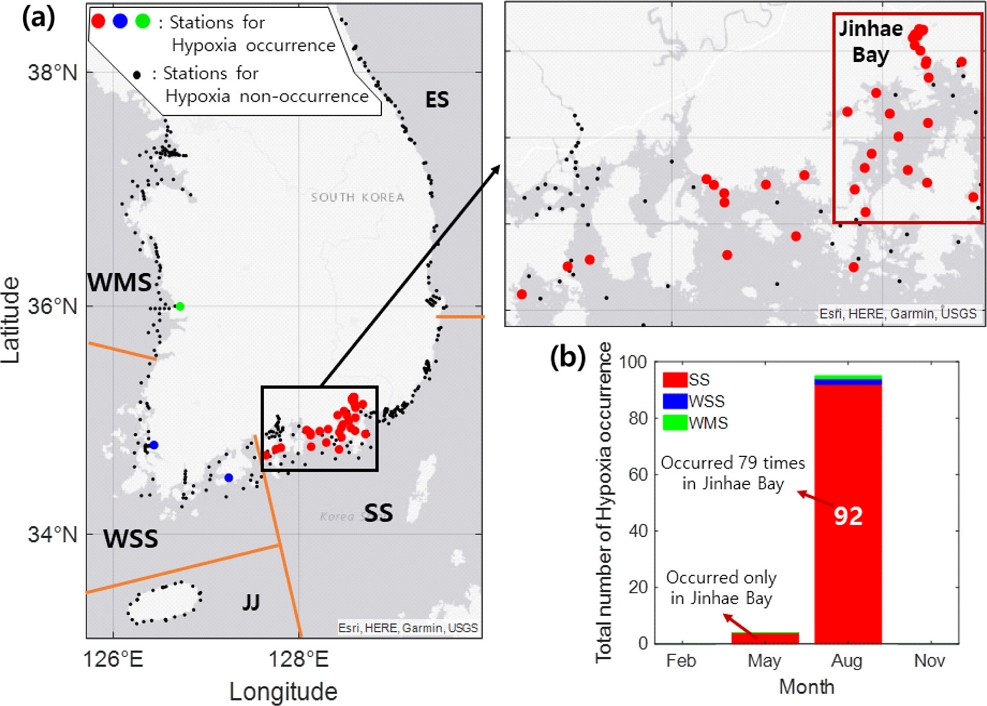
(a) Location of stations where hypoxia water mass occurred in five ecological zones(SS: South sea, ES: East sea, WSS: West-south sea, WMS: West-middle sea, JJ: Jeju) and (b) total number of hypoxia occurrence by quarter from Feb 2012 to Feb 2021.
관측 기간 동안 총 99건의 빈산소수괴가 발생하였다. 2월과 11월에는 빈산소수괴가 관측되지 않았으며, 5월에는 4건, 8월에는 95건의 빈산소수괴가 관측되었다. 8월에 관측된 95건의 빈산소수괴 중 92건은 대한해협 정점에서 관측되었으며, 이 중 79건은 진해만 내에서 발생하였다. 또한, 5월에 발생한 4건의 빈산소수괴는 모두 진해만에서 발생하였다.
여름철 진해만의 상대적으로 높은 빈산소수괴 발생 빈도는 여름철 성층 형성과 높은 오염 부하량, 그리고 반폐쇄적인 지형적 특성에 기인한 것으로 판단된다. 여름철 높은 기온과 일사량에 의해 형성된 성층은 저층으로의 용존 산소 공급을 억제한다. 진해만의 반폐쇄적 특성으로 인한 낮은 해수 교환율로 인해 육지로부터 유입된 다량의 유기물은 저층으로 퇴적되어 산소를 소모한다. 연 누적 강수량의 2012~2021년 평균값은 창원과 통영 각각 1455.6, 1691.8 mm로 전국 평균보다 13.8, 32.3% 높았으며, 진해만의 육지 기원 오염 부하량이 상대적으로 많았을 것으로 예상된다(KMA[2023]).
서해중부와 서남해역에서는 10년 관측 자료 중 단 3건의 빈산소수괴가 관측되었으며, 동해와 제주에서는 1건도 관측되지 않았다. 이는 분기별 정점 조사 자료의 낮은 시공간적 해상도로 인해 실제로 발생한 빈산소수괴를 관측하지 못한 것으로 판단된다. 빈산소수괴에 대한 빠른 대응을 위해서는 높은 시공간적 해상도의 저층 DO 농도 산출 기술이 필요하다.
3.2 저층 DO 농도 산출을 위한 기계학습 모델 개발 결과
예측변수의 선형회귀 p-value와 random forest 기반의 feature importance를 Table 2에 나타내었다. Rrs412, Rrs443, Rrs490, Rrs555, 그리고 SST의 p-value는 0.05 이하로 예측변수로서 유의하였다. Feature importance가 1.5 이상인 변수는 Rrs490, Rrs555, Rrs660, Rrs680, Chl.a, DAC, POC, SST로 나타났다. SST와 Chl.a의 feature importance는 각각 10.84, 2.68로 다른 변수들에 비해 상대적으로 높게 나타났다. 표층 수온은 성층의 형성 여부와 두께를 결정하는 중요 요인 중 하나이며, 수온은 해수의 산소 용해도와 음의 상관성을 보인다(Wilson[2010]). Chl.a는 식물플랑크톤의 생체량을 나타내는 지표로, 식물플랑크톤의 광합성은 해양 1차 생산의 95% 이상을 차지한다(Edward et al.[2021]). 이와 같은 이유로 SST와 Chl.a의 feature importance가 다른 변수들에 비해 상대적으로 크게 나타난 것으로 판단된다.

Results of predictor evaluation based on the t-test p-value of linear regression and feature importance of random forest
예측변수 평가 결과를 바탕으로 네 개의 예측변수 조합을 고려하여 최적 예측변수 조합을 선별하였다. 먼저, 1) p-value가 0.05 이하인 Rrs412, Rrs443, Rrs490, Rrs555, SST, 2) feature importance가 1.5 이상인 Rrs490, Rrs555, Rrs660, Rrs680, Chl.a, DAC, POC, SST, 3) p-value가 0.05 이하이면서 feature importance가 1.5 이상인 Rrs490, Rrs555, SST, 4) 그리고 모든 변수를 사용한 조합이 고려되었다.
베이지안 최적화로 최적화된 모델 후보들의 hyperparameter와 목적함수 값들을 Table 3에 나타내었다. GPR로 산출한 저층 DO 농도와 관측값 간의 R2는 0.69로 모든 모델 중 가장 높은 재현도를 보였다. 또한, GPR의 RMSE, MSE, MAE는 각각 0.96, 0.92, 0.65로 모델 중 가장 낮은 오차를 보였다. 모든 목적함수에서 가장 우수한 결과를 보인 GPR이 저층 DO 농도 산출을 위한 최적 모델로 선별되었다.

Optimal hyperparameters and objective function values(R2, RMSE, MSE, and MAE) for Decision tree, Support vector machine, Neural network, and Gaussian process regression
최적 모델로 선별된 GPR의 형태는 hyperparameter 중 커널 함수의 종류에 따라 결정되며, 지수(exponential), 제곱 지수(squaredexponential), 2차 유리(rationalquadratic), matern32, matern52 중 지수 커널 함수가 최적 커널 함수로 결정되었다. 지수 커널 함수는 다음과 같다.
| (5) |
| (6) |
여기서, K는 커널 함수, σf와 σl는 각각 signal standard deviation과 length scale를 의미한다.
예측변수 조합별 목적함수 값을 Table 4에 나타내었다. 모든 변수를 예측변수로 사용했을 때 R2는 0.69로 가장 높게 나타났다. 또한, RMSE, MSE, 그리고 MAE는 각각 0.96, 0.92, 0.65로 모든 예측변수 조합 중 가장 낮은 오차를 보였다. 이에 따라 모든 변수를 사용한 예측변수 조합을 최적 예측변수로 선별하였으며, 학습된 모델을 Model-UP1으로 정의하였다.
해양의 DO 농도는 물리적 이류·확산과 생물 호흡, 유기물 분해와 같은 생화학적 과정들에 의해 비선형적으로 결정된다. 특히, 연안 해역은 육지로부터의 오염 부하와 반폐쇄적 특성에 의한 높은 체류시간 등 그 지리적 특성으로 인해 저층 DO 농도를 산출하는 것은 매우 어렵다. 연안의 저층 DO 농도 산출을 위해서는 다양한 변수가 고려되어야 하며, 그 결과로 모든 변수를 사용한 예측변수 조합이 가장 높은 재현도를 보인 것으로 판단된다(Park and Kim[2022]).
Model-UP1과 ‘예측변수 생성’ 기법이 적용된 Model-UP2, 그리고 ‘생태구별 모델 분리’ 기법을 포함하여 모든 개선 기법이 적용된 Model-UP3의 목적함수 값들을 Table 5에 나타내었다. 그 목적함수 값들은 전체 정점 자료와 대한해협 정점 자료로 구분하여 나타내었다. 전체 정점 자료로 평가한 Model-UP2의 R2는 0.76으로 Model-UP1 대비 10.1% 개선된 결과를 보였다. Model-UP3의 R2는 0.84로 Model-UP1 대비 21.7% 개선되었으며, 또한, RMSE, MSE, MAE는 각각 28.3, 46.3, 32.3% 개선된 결과를 보였다. 특히, 빈산소수괴가 자주 발생했던 대한해협 정점 자료로 평가한 Model-UP3의 MSE는 0.47로 Model-UP1 대비 61.8% 개선되는 결과를 보였다. 모든 개선 기법이 적용된 Model-UP3는 모든 모델 중 가장 높은 재현도를 보였으며, 이는 저층 DO 농도 관측값과 산출값 간의 1:1 산점 비교 그래프에서도 확인할 수 있었다(Fig. 3).

Objective function values (R2, RMSE, MSE, and MAE) for each model with applied improvement techniques. Model-UP1: model with applied ‘Optimal model selection’ and ‘Optimal predictor selection’, Model-UP2: Model-UP1 with applied ‘Predictor generation’, Model-UP3: Model-UP2 with applied ‘Separation by ecological zones’
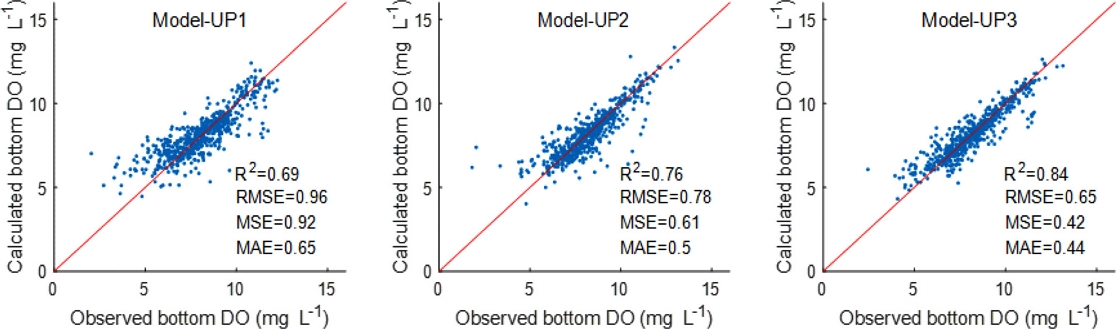
Validation results of the improved models for estimating bottom dissolved oxygen(DO) concentration. Model-UP1: model with applied ‘Optimal model selection’ and ‘Optimal predictor selection’, Model-UP2: Model-UP1 with applied ‘Predictor generation’, Model-UP3: Model-UP2 with applied ‘Separation by ecological zones’.
최종 모델의 저층 DO 농도 산출값은 관측값과 높은 재현도를 보였다. 하지만, 빈산소수괴 발생 자료의 부족으로 본 모델이 실제 빈산소수괴 발생 탐지가 가능한지에 대해서는 불확실성이 존재한다. 실시간 빈산소수괴 발생 탐지를 위해서는 관측 자료를 보충하고, 위성 해색 자료들과 DO 농도 자료 간의 맵핑 과정에서 발생하는 오차를 줄일 필요가 있다. 해양환경측정망 자료와 함께 국립수산과학원의 어장환경모니터링 자료 등 다른 관측 자료들을 추가로 활용한다면 실시간 빈산소수괴 발생 탐지의 불확실성을 줄일 수 있을 것이다. 또한, 위성 해색 자료 간의 보간 과정을 거치지 않고 각각의 위성 자료를 DO 농도 자료에 맵핑한다면 보간 과정에서 발생하는 오차를 줄일 수 있을 것이다. 이 외에도 원격반사도의 음수값 처리를 통해 모델 개선이 가능할 것이다. 바다의 반사도는 육지에 비해 낮아 대기 보정 과정에서 개념적으로는 불가능한 음수값이 발생할 수 있다. 본 연구에서는 학습자료 수의 부족으로 원격반사도의 음수값을 원자료 그대로 사용하였으나, 이러한 음수값을 제거하거나 전처리함으로써 모델의 성능을 개선할 수 있을 것이다.
4. 결 론
국내 연안에서는 매년 여름철 빈산소수괴가 발생하여 그로 인한 어업 피해가 최근까지도 잇따르고 있다. 빈산소수괴에 대한 빠른 대응을 위해 시공간적 고해상도 연안 저층 DO 농도의 수요는 증가하고 있으나, 국내에는 아직 관련 모니터링 시스템이 없다. 본 연구에서는 위성 해색 자료와 해양환경측정망의 DO 농도 자료를 사용하여 시공간적 고해상도의 연안 저층 DO 농도 산출을 위한 모델을 개발하였다. 정확도 개선 과정을 거친 최종 모델로 산출한 저층 DO 농도와 관측치 간의 R2는 0.84로 높은 재현성을 보였다. 본 기술은 시공간적 고해상도의 연안 저층 DO 농도를 제공할 수 있을 것이며, 더 나아가 실시간 빈산소수괴 발생 탐지를 위한 기초 기술로 활용될 수 있을 것으로 기대된다.
Acknowledgments
이 논문은 2023년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(Grant 2021R1I1A30603741361782064340103).
References
-
Breitburg, D., Levin, L. A., Oschlies, A., Grégoire, M., Chavez, F.P., Conley, D.J., Garcon, V., Gilbert, D., Gutierrez, D., Isensee, K., Jacinto, G.S., Limburg, K.E., Montes, I., Naqvi, S.W.A., Pitcher, G.C., Rabalais, N.N., Roman, M.R., Rose, K.A., Seibel, B.A., Telszewski, M., Yasuhara, M. and Zhang, J., 2018, Declining oxygen in the global ocean and coastal waters, Sci., 359(6371), eaam7240.
[https://doi.org/10.1126/science.aam7240]

-
Chan, F., Barth, J.A., Lubchenco, J., Kirincich, A., Weeks, H., Peterson, W.T. and Menge, B.A., 2008, Emergence of anoxia in the California current large marine ecosystem, Sci., 319(5865), 920-920.
[https://doi.org/10.1126/science.1149016]

-
Charbuty, B. and Abdulazeez, A., 2021, Classification based on decision tree algorithm for machine learning. Journal of Applied Science and Technology Trends, 2(1), 20-28.
[https://doi.org/10.38094/jastt20165]

-
Conley, D.J., Carstensen, J., Ærtebjerg, G., Christensen, P.B., Dalsgaard, T., Hansen, J.L. and Josefson, A.B., 2007, Long‐ term changes and impacts of hypoxia in Danish coastal waters, Ecol. Appl., 17(5), 165-184.
[https://doi.org/10.1890/05-0766.1]

-
Duffus, J., 1993, Glossary for chemists of terms used in toxicology (IUPAC Recommendations 1993), Pure Appl. Chem., 65(9), 2003-2122.
[https://doi.org/10.1351/pac199365092003]

-
Edward, J.P., Jayanthi, M., Malleshappa, H., Jeyasanta, K.I., Laju, R.L., Patterson, J., Diraviya Raj, K., Mathews, G., Marimuthu, A.S. and Grimsditch, G., 2021, COVID-19 lockdown improved the health of coastal environment and enhanced the population of reef-fish, Mar. Pollut. Bull., 165, 112124.
[https://doi.org/10.1016/j.marpolbul.2021.112124]

-
Guo, H., Huang, J.J., Zhu, X., Wang, B., Tian, S., Xu, W. and Mai, Y., 2021, A generalized machine learning approach for dissolved oxygen estimation at multiple spatiotemporal scales using remote sensing, Environ. Pollut., 288, 117734.
[https://doi.org/10.1016/j.envpol.2021.117734]

-
Howarth, R., Chan, F., Conley, D.J., Garnier, J., Doney, S.C., Marino, R. and Billen, G., 2011, Coupled biogeochemical cycles: eutrophication and hypoxia in temperate estuaries and coastal marine ecosystems, Front. Ecol. Environ., 9(1), 18-26.
[https://doi.org/10.1890/100008]

-
Kim, Y.H., Son, S., Kim, H.C., Kim, B., Park, Y.G., Nam, J. and Ryu, J., 2020, Application of satellite remote sensing in monitoring dissolved oxygen variabilities: A case study for coastal waters in Korea, Environ. Int., 134, 105301.
[https://doi.org/10.1016/j.envint.2019.105301]

- KMA(Korea Meteorological Administration), Automated Synoptic Observing System(ASOS), https://data.kma.go.kr/cmmn/main.do, , 2023 (accessed 2023.07.22.).
- KOEM(Korea Marine Environment Management Corporation), Marine Environment Observation & Survey(해양환경 관측&조사), https://www.meis.go.kr/mei/observe/port.do, , 2023 (accessed 2023.01.13.).
- Lawrence, S., Giles, C. L. and Tsoi, A. C., 1997, Lessons in neural network training: Overfitting may be harder than expected, in proc. of the Fourteenth National Conference on Artificial Intelligence, AAAI-97, AAAI Press, Menlo Park, California, United States, 540-545.
- NOAA(National Oceanic and Atmospheric Administration), Ocean Color Data, https://oceandata.sci.gsfc.nasa.gov/, , 2023 (accessed 2023.02.22.).
-
Park, S. and Kim, K., 2022, Preliminary Study on the Reproduction of Dissolved Oxygen Concentration in Jinhae Bay Based on Deep Learning Model, J. Korean Soc. Mar. Environ. Saf., 28(2), 193-200.
[https://doi.org/10.7837/kosomes.2022.28.2.193]

-
Park, S. and Kim, K., 2023, Monitoring of Changes in the Dissolved Oxygen Concentration and Phytoplankton Bloom in the Coast of South Korea using COMS and Gaussian Process Regression, J. Korean Soc. Mar. Environ. Energy, 26(1), 57-65.
[https://doi.org/10.7846/JKOSMEE.2023.26.1.57]

-
Park, S., Yoon, S., Lee, I., Kim, B. and Kim, K., 2021, Prediction of Stratification Strength and Dissolved Oxygen due to Cold Discharge of Jinhae Bay in Summer, J. Korean Soc. Mar. Environ. Energy, 24(3), 106-118.
[https://doi.org/10.7846/JKOSMEE.2021.24.3.106]

-
Shao, J., Huang, S., Chen, Y., Qi, J., Wang, Y., Wu, S., Liu, R. and Du, Z., 2023, Satellite-Based Global Sea Surface Oxygen Mapping and Interpretation with Spatiotemporal Machine Learning, Environ. Sci. Technol., 58(1), 498-509.
[https://doi.org/10.1021/acs.est.3c08833]

-
Stramma, L., Johnson, G.C., Sprintall, J. and Mohrholz, V., 2008, Expanding oxygen-minimum zones in the tropical oceans, Sci., 320(5876), 655-658.
[https://doi.org/10.1126/science.1153847]

-
Vaquer-Sunyer, R., and Duarte, C.M., 2008, Thresholds of hypoxia for marine biodiversity, Proc. of the Natl. Acad. of Sci., 105(40), 15452-15457.
[https://doi.org/10.1073/pnas.0803833105]

-
Wilson, P.C., 2010, Water Quality Notes: Dissolved Oxygen: SL313/SS525, 1/2010. EDIS, 2010(2).
[https://doi.org/10.32473/edis-ss525-2010]

-
Yin, K., Lin, Z. and Ke, Z., 2004, Temporal and spatial distribution of dissolved oxygen in the Pearl River Estuary and adjacent coastal waters, Cont. Shelf Res., 24(16), 1935-1948.
[https://doi.org/10.1016/j.csr.2004.06.017]

-
Zhang, Y., 2012, Support vector machine classification algorithm and its application, in proc. of the In Information Computing and Applications: Third International Conference, ICICA 2012, Chengde, China, 179-186.
[https://doi.org/10.1007/978-3-642-34041-3_27]