좌초 선박의 이초력 추정 기법 개발 및 모형시험을 통한 검증 연구

1. 서 론

우리나라에서는 매년 약 3,000건의 해양사고가 꾸준히 보고되고 있으며, 이 중 선박이 암초, 모래톱, 얕은 해저 지형 등에 접촉하여 선체가 손상되는 좌초 사고가 일정 비율을 차지하고 있다. 해양 운송 산업에서 선박의 좌초 사고는 빈번하게 발생하며, 이는 심각한 경제적 손실과 환경 파괴를 초래할 수 있는 주요 사고 중 하나이다. 특히, 좌초된 선박을 이초하는 과정은 매우 복잡하고 위험성이 높아, 이를 성공적으로 수행하기 위해서는 과학적이고 체계적인 접근이 필수적이다. 이초 작업의 성공 여부는 선박에 작용하는 이초력을 얼마나 정확하게 추정하느냐에 달려 있으며, 이초력은 선박의 구조적 특성, 해저 지형, 조석간만 등 다양한 해양 조건에 의해 영향을 받는다. 이러한 요소들을 종합적으로 고려한 이초력의 정확한 추정은 선박 구난 작업의 필수 요소이다.

기존의 연구들은 선박의 좌초 및 구조적 손상을 분석하기 위한 다양한 방법을 제시하였다. 예를 들어, Simonsen[1997]은 선저가 암초 위를 수평방향으로 이동하였을 때 선저의 구조 손상, 수평 및 수직 방향 힘을 계산하기 위한 해석적 모델을 개발하였다. 이후 이 모델은 대규모 실험과 실제 좌초 사건을 통해 검증되었으며, 손상 예측의 정확성을 입증하였다. Pineau et al.[2022]는 선박 좌초 시 손상을 신속하게 평가하기 위한 수치적 도구를 개발하여 다양한 좌초 상황에서의 구조적 손상을 분석하였으며, Pineau and Le Sourne [2023]는 전후 동요(surge)와 상하 동요(heave) 운동을 동시에 고려한 구조적 저항력 분석을 통해 좌초 손상의 해석적 모델링을 제안하였다. Lee et al.[2022]는 좌초된 선박의 이초 작업을 위한 정적 평형기반의 자세 계산 방법을 제안하였지만, 폭방향을 고려하지 않은 2차원 해석에 그쳤다.

이와 더불어, 좌초 사고 시의 이초 계획과 위험 평가도 중요한 연구 주제로 다루어져 왔다. Hussein et al.[2016]는 이중 선체 탱커의 신속한 이초를 위해서 구조 강도를 포함한 중량 조절 작업 방향을 제시하였으며, Youssef and Paik[2018]은 기존의 선박 좌초 사고 통계를 활용하여 좌초 결과에 영향을 미치는 매개변수를 설정하고, 각 매개변수별 빈도를 확률 밀도 함수로 공식화 하였다. 이를 통해서 좌초 사고의 시나리오를 생성하여 사고 위험성을 분석하고 관리하는 방안을 제시하였다. Mazaheri et al.[2016]는 좌초사고의 증거 데이터 및 전문가 판단을 기반으로 한 확률적 위험 모델을 개발하여 사고 발생 확률을 평가하고, 이에 대한 적절한 위험 관리방안을 제안하였다.

모형시험을 통해 얻어진 실험적 데이터는 이론적 모델과 수치 해석의 검증에 중요한 역할을 한다. Bennett and Phillips[2017]는 좌초 사고 후 침수수가 선박의 운동과 구조적 반응에 미치는 영향을 실험적으로 조사하였으며, 선박 설계 규정과 비교하여 파도에 의해서 유기되는 수직 굽힘모멘트의 안전 범위에 대한 추가적인 평가가 필요함을 언급하였다. Zhu et al.[2024]는 공학수조에서 소형 선박 모형을 사용한 좌초 실험을 수행하였으며, 이를 통해 선저 손상 메커니즘과 에너지 소산 과정을 분석하여 이론적 예측을 뒷받침하였다.

위의 연구들은 주로 선박의 좌초로 인한 구조 손상 분석이나 이초 계획에 따른 위험성 평가에 초점을 맞추고 있다. 그러나 실제 좌초 상황이 발생하였을 때는 선박의 이초 방법을 결정하기 위한 초기 지반반력 및 이초력의 정확한 추정이 필요하며, 이를 바탕으로 해상 크레인이나 예인선의 배정이 이루어져야 한다. 또한, 적절한 예인 시점 및 이초 계획을 결정하기 위해서는 조석간만에 의한 수심의 변화나 중량조절 작업에 따른 이초력 변화를 빠르고 정확하게 계산할 수 있는 방법이 필요하다. 따라서 본 연구에서는 선박의 정유체력 데이터가 포함된 배수량 표(hydrostatic table), 본진 표(Bonjean table), 복원력 교차곡선 표(cross-curve table)를 활용하여 좌초 선박의 이초력을 추정하는 기법을 개발하였으며, 다양한 좌초 상황과 조석간만, 중량 조절 작업에 따른 변화를 반영할 수 있는 프로그램으로 구현되었다. 개발된 기법은 상용 구난 해석 프로그램인 HECSALV (Herbert-ABS[2024])와 비교를 통해서 높은 정확도를 확인하였다. 또한, 선박해양플랜트연구소 심해공학수조(부산)에서 이초력 추정을 위한 모형시험을 수행하였으며, 이 과정에서 좌초 위치, 수심, 중량 이동에 따른 이초력 변화 양상을 분석하였다. 이러한 실험적 검증을 통해서 개발된 기법의 실효성과 신뢰성을 확인하였다. 아울러, 대표적인 구난 해석 참고 문헌인 Salvage manual(U.S. Navy[2013])의 지반반력 추정 식을 분석하고, 횡동요 영향을 반영할 수 있도록 수정한 식을 제안하였다. 이와 같은 연구를 통해 개발된 기법은 다양한 좌초 상황에서 이초력을 정확하게 추정할 수 있으며, 이를 바탕으로 보다 안전하고 효과적인 선박 구난 작업을 수행하는 데 기여할 것으로 기대된다.

2. 좌초 선박 이초력 추정 기법 개발

좌초된 선박의 이초 여부 판단을 위해서는 초기 이초력(freeing force) 추정이 필수적이며, 정확한 이초력 산출을 위해서는 지반반력(ground reaction force)을 정확하게 추정하는 것이 중요하다. 일반적으로 자유롭게 떠 있는 선박은 중력과 부력의 두 가지 힘이 정적 평형상태를 이루게 되어 물에 떠있을 수 있다. 반면 좌초된 선박은 해저 지형과 접함으로 인해서 선박의 자세가 바뀌게 되며, 이로 인해서 손실된 부력만큼 지반반력이 작용하게 된다. 따라서 좌초된 선박은 중력, 부력 및 지반반력의 세 힘의 평형상태를 고려함으로써 힘 및 모멘트 평형식을 통해서 지반반력의 크기 및 작용점을 도출할 수 있다. 이초력은 아래의 식과 같이 지반반력과 해저지형 마찰계수의 곱(U.S. Navy[2013])으로 정의되며, 좌초된 선박을 수평방향으로 끌어내는데 필요한 힘을 의미한다.

여기서 F = 이초력, 좌초된 선박을 끌어내기 위한 수평방향 힘[ton]
R = 지반반력, 수직상방으로 작용하는 힘[ton]
μ = 마찰계수, 해저지형의 종류에 따라서 결정

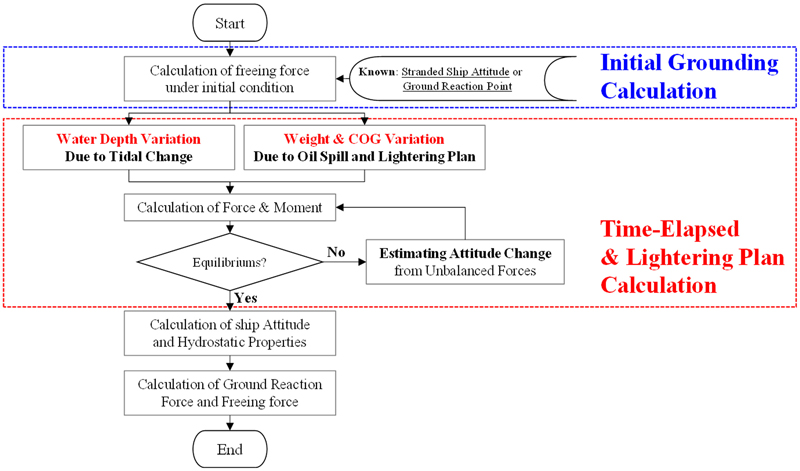
본 연구에서 좌초된 선박의 이초 작업 해석은 아래와 같이 3단계로 구분하였다. 첫 번째 단계는 좌초사고가 난 직후 초기 이초력을 추정하는 단계(초기 좌초 계산)이며, 두 번째 단계는 조석 간만에 의한 수심의 변화, 기름 유출에 따른 중량 변화에 따라서 이초력이 변화되는 양상을 확인하는 단계(시간 경과 계산)이다. 세 번째 단계는 좌초된 선박에서의 화물 추가, 이동, 제거를 통해서 변화되는 이초력을 확인하는 단계(중량 조절 작업)이며, 이러한 일련의 과정을 통해서 최적의 이초 시점 및 이초 방법을 결정할 수 있다. 이어지는 장에서 각 단계별 계산 방법을 자세히 서술 한다.

2.1 초기 좌초 계산

앞서 언급한 바와 같이 좌초된 선박에 작용하는 힘은 중력, 부력, 그리고 손실된 부력의 크기만큼의 지반반력으로 구성된다. 중력은 수직하방으로 작용하는 힘이며, 부력과 지반반력은 수직상방으로 작용하는 힘으로, 이 세 가지 힘의 정적 평형상태를 고려하여 지반반력의 크기와 작용점을 구하게 된다.

선박에 작용하는 중력의 크기 및 작용점은 좌초 직전의 선박의 경하중량과 모든 화물의 중량을 더해서 구한다. 선박에 작용하는 부력의 크기 및 작용점은 3개의 정유체력 표(배수량 표, 복원력 교차곡선 표, 본진 표)를 활용하여 계산한다. 배수량 표는 흘수에 따른 정유체력 정보(배수량, 부면심, 부력중심등)들이 포함되어 있으며, 복원력 교차곡선 표는 배수량과 횡경사에 따른 KN값이 포함되어 있다. 본진 표는 일종의 오프셋 표(offset table)이며, 각 섹션에서의 포인트 정보, z방향 적분 시 단면 부력 및 부력 중심 값 등이 포함되어 있다. 만약 배수량 표가 선박의 흘수, 종경사, 횡경사에 따른 정유체력 정보가 포함되어 있다면 이를 사용하여 선박의 특정 자세에서의 부력 및 부력 중심 값을 도출할 수 있다. 다만 배수량 표는 등흘수 (evenkeel) 상태에서 흘수에 따른 정유체력 정보를 제공하는 것이 일반적이다. 따라서 본 연구에서는 배수량 표가 등 흘수 상태에서의 정보만 포함되어 있다고 가정하며, 선박의 자세가 등흘수이고 횡동요가 없는 제한된 경우에만 사용한다. 선박의 자세가 등흘수가 아닌 경우는 본진 표와 복원력 교차곡선 표를 사용하여 선박의 특정 자세에서의 부력 및 부력 중심 값을 도출한다.

본 연구에서는 좌초 상황을 ‘일점(one-point) 좌초 상황’, ‘이점(two-point) 좌초 상황’, ‘평평한 지반(flat-bottom) 좌초 상황’의 3가지로 구분하였다. 일점 및 이점 좌초 상황은 선저의 하나 혹은 두개의 지점이 해저지형에 접했다고 가정하며, 그 지점의 위치 및 지반반력을 추정하게 된다. 평평한 지반 좌초 상황은 모래톱과 같은 평평한 지반에 선박이 좌주된 상태를 의미하며, 좌주 영역을 설정하고 영역에서의 지반반력 분포를 계산한다. 각각의 상황에서의 지반반력 계산 방법은 다음과 같다.

2.1.1 일점 좌초 상황에서의 지반반력 계산

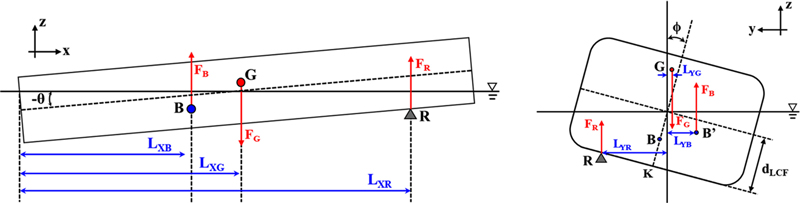
선박이 해저지형의 한 지점에 좌초된 경우 지반반력의 크기 및 작용점은 선박에 작용하는 힘의 평형식을 통해서 계산한다. Fig. 1은 일점 좌초 상황에서 선박에 작용하는 힘의 개략도이며, 힘 및 모멘트 평형식은 아래와 같다.

$\[ \begin{array}{l}\text{ Force : }{F}_B+F_G+F_R=0\\ \text{ Trim Moment : }{F}_B{L}_{XB}+F_G{L}_{XG}+F_R{L}_{XR}=0\\ \text{ Heel Moment : }{F}_B{L}_{YB}+F_G{L}_{YG}+F_R{L}_Y=0\end{array} \]$

(2)

$\[ \begin{array}{l}{L}_{XB}=X_B\mathrm{c}\mathrm{o}\mathrm{s}\theta -\left(d_{AP}-Z_B\right)\mathrm{s}\mathrm{i}\mathrm{n}\theta L_{YB}=-KN+d_{LCF}\mathrm{s}\mathrm{i}\mathrm{n}\varphi \\ L_{XG}=X_G\mathrm{c}\mathrm{o}\mathrm{s}\theta -\left(d_{AP}-Z_G\right)\mathrm{s}\mathrm{i}\mathrm{n}\theta L_{YG}=Y_G\mathrm{c}\mathrm{o}\mathrm{s}\varphi -\left(Z_G-d_{LCF}\right)\mathrm{s}\mathrm{i}\mathrm{n}\varphi \\ L_{XR}=X_R\mathrm{c}\mathrm{o}\mathrm{s}\theta -\left(d_{AP}-Z_R\right)\mathrm{s}\mathrm{i}\mathrm{n}\theta L_{YR}=Y_R\mathrm{c}\mathrm{o}\mathrm{s}\varphi +d_{LCF}\mathrm{s}\mathrm{i}\mathrm{n}\varphi \end{array} \]$

(3)

여기서 F_B, F_G, F_R = 선박에 작용하는 부력, 중력, 지반반력[ton]
X_B, Z_B = 물체 고정 좌표계에서의 부력중심점 위치[m]
X_G, Y_G, Z_G =물체 고정 좌표계에서의 무게중심점 위치[m]
X_R, Y_R, Z_R = 물체 고정 좌표계에서의 지반반력 위치[m]
d_AP, d_LCF = AP, LCF 지점에서의 흘수[m]
KN =선박의 기선으로 부터 부력 작용선까지의 수직거리[m]
θ, φ = 선박의 종경사 및 횡경사 각도

Fig. 1.

Schematic diagram of force acting in a single-point grounding situation.

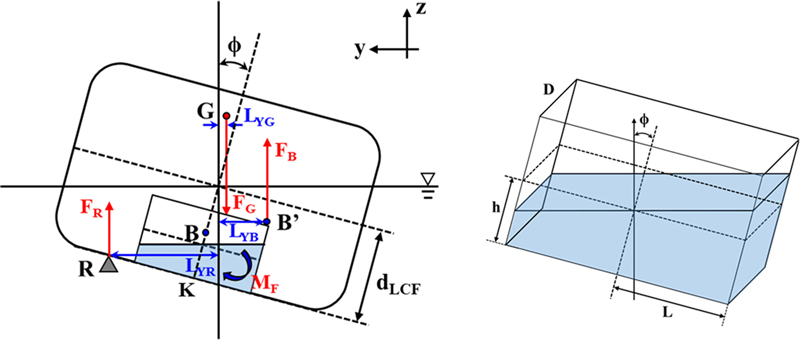
Fig. 2와 같이 화물창에 자유표면이 포함된 액체화물이 포함된 경우, 선박의 횡경사로 인한 추가적인 모멘트가 발생한다. 이를 반영하기 위해서 아래의 식과 같이 자유표면에 의한 횡경사 모멘트, M_F를 추가하였다.

$\[ \mathrm{H}\mathrm{e}\mathrm{e}\mathrm{l}\mathrm{ }\mathrm{M}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} : F_B{L}_{YB}+F_G{L}_{YG}+F_R{L}_{YR}+M_F=0 \]$

(4)

$\[ M_F={\rho }_w{I}_T\mathrm{s}\mathrm{i}\mathrm{n}\varphi \]$

(5)

여기서 ρ_w = 액체화물 밀도[kg/m³]
I_T = 자유표면 모멘트[m⁴]

Fig. 2.

Schematic diagram of heeling moment from liquid cargo free-surface effect.

2.1.2 이점 좌초 상황에서의 지반반력 계산

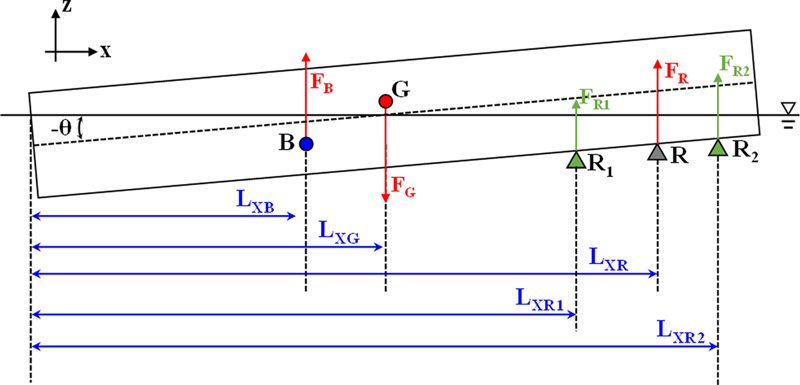
두 지점에 좌초된 상황에서는 두 지반반력의 작용점의 y좌표는 동일하다고 가정하며, Fig. 3과 같이 두 좌초지점의 x좌표 정보(L_XR1, L_XR2)가 추가로 필요하다. 일점 좌초상황에 대해서 먼저 계산을 수행하여 지반반력의 크기 및 작용점(F_R, L_XR, L_YR)을 계산한 후, 아래의 힘 및 모멘트 평형식에 맞춰서 두 점으로 힘을 분배한다.

$\[ \begin{array}{l}\text{ Force : }{F}_R=F_{R1}+F_{R2}\\ \text{ Trim Moment : }{F}_R{L}_{XR}=F_{R1}{L}_{XR1}+F_{R2}{L}_{XR2}\\ \text{ Heel Moment : }{F}_R{L}_{YR}=F_{R1}{L}_{YR1}+F_{R2}{L}_{YR2}\end{array} \]$

(6)

$\[ \Rightarrow F_{R1}=\frac{F_R\left(L_{XR}-L_{XR2}\right)}{L_{XR1}-L_{XR2}},F_{R2}=\frac{F_R\left(L_{XR}-L_{XR1}\right)}{L_{XR2}-L_{XR1}} \]$

(7)

여기서 F_R1, F_R2=두 지점에서의 지반반력[ton]
L_XR1, L_XR2=두 지반반력 지점의 x좌표, 입력값[m]

Fig. 3.

Schematic diagram of force acting in a two-point grounding situation.

2.1.3 평평한 지반(Simple shelf) 좌초 상황에서의 지반반력 계산

평평한 지반 영역은 직사각형으로 가정하며, 직사각형의 네 꼭지점의 위치(x_s, x_f, y_s, y_f) 및 직사각형에서 x, y 방향으로의 분할 개수(n_x, n_y)의 정보가 추가로 필요하다. 지반반력은 Fig. 4와 같이 사다리꼴 형태로 위치에 따라서 선형적으로 변한다고 가정하며, 기울기를 a, y절편을 b라고 두어 a, b값을 계산한다. 앞선 조건과 마찬가지로 일점 좌초 조건에 대해서 먼저 계산하여 지반반력의 크기 및 작용점(F_R, L_XR, L_YR )을 계산한 후, 힘과 모멘트 평형식에 맞춰서 힘을 분배한다.

Fig. 4.

Schematic diagram of forces acting in a simple shelf grounding situation.

- 힘 및 모멘트 평형식

$\[ \begin{array}{l}{F}_1+F_2+\cdots +F_n=F_R\\ F_1\cdot x_1+F_2\cdot x_2+\cdots +F_n\cdot x_n=F_R\cdot L_{XR}\end{array}\Rightarrow \left[\begin{array}{cccc}1& 1& \cdots & 1\\ x_1& x_2& \cdots & x_n\end{array}\right]\left[\begin{array}{c}{F}_1\\ F_2\\ ⋮\\ F_n\end{array}\right]=\left[\begin{array}{c}{F}_R\\ F_R{L}_{XR}\end{array}\right] \]$

(8)

- 지반반력이 선형적으로 변한다고 가정

$\[ \left[\begin{array}{c}{F}_1\\ F_2\\ ⋮\\ F_n\end{array}\right]=\left[\begin{array}{c}a{x}_1+b\\ a{x}_2+b\\ ⋮\\ a{x}_n+b\end{array}\right]=\left[\begin{array}{cc}{x}_1& 1\\ x_2& 1\\ ⋮& ⋮\\ x_n& 1\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right] \]$

(9)

- Eq. (9)를 Eq. (8)에 대입하여, 기울기, a, y절편, b계산

$\[ \left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^n x_{i}n\\ \sum _{i=1}^n x_{i}n\end{array}\right]\left[\begin{array}{c}{F}_R\\ F_R{L}_{XR}\end{array}\right] \]$

(10)

위의 수식은 x방향으로의 분포를 계산하는 수식이며, y방향으로의 분포 또한 동일한 형태의 힘 및 모멘트 평형식을 적용하여 계산 할 수 있다. 이후 각각의 축 방향으로 지반반력이 선형적으로 변한다는 가정을 적용하여 직사각형 영역의 전체 지지점에 힘을 분배한다.

한 가지 주의해야 할 점은, 위의 방법을 적용하여 지반반력 분포를 계산하는 경우, 평평한 지반 영역을 어떻게 설정하는지에 따라서 지반반력이 음의 값이 나오는 경우가 발생하며, 이는 물리적으로 합당하지 않다. 지반반력이 음의 값이 나오는 경우에 대해서는 추가적인 보정을 포함하였다.

2.2 시간 경과 및 중량 조절 작업 계산

지반반력 및 이초력에 큰 영향을 미치는 요소 중 하나는 조석간만으로 인한 수심 변화이다. 수심이 깊어질 경우 지반반력이 감소하며 자연스럽게 부유 상태로 전환되기도 한다. 또한, 좌초 사고로 인해서 화물창이 손상된 경우 시간이 지남에 따라 기름이 유출 되고 해수가 유입되면서 지반반력과 이초력에 변화를 초래할 수 있다. 따라서, 시간 경과에 따른 영향은 조석간만으로 인한 수심 변화, 기름 유출 및 해수 유입으로 인한 중량변화를 고려하였다. 중량 조절 작업은 이초 작업의 효율성을 극대화하기 위해 필수적인 요소이며, 특정 시점에서 이초 작업을 수월하게하기 위해서 선박의

위에서 언급한 세 가지 상황은 구체적인 조건은 다르지만 계산하는 방법은 Fig. 5와 같이 동일한 프로세스를 따른다. 먼저 초기 좌초 상황을 계산하여 지반반력의 크기 및 작용점을 계산한다. 그후 조석간만에 의한 수심변화 혹은 기름 유출 및 중량 조절 작업에 의한 중량 및 무게 중심 변화를 입력 값으로 받은 후 세 가지 힘 성분(중력, 부력, 지반반력)에 의한 힘과 모멘트 평형을 계산한다. 수심 혹은 중량 변화로 인해서 불균형력이 발생하면, 이로부터 선박의 자세 변화를 추정한다. 이후 변화된 자세를 바탕으로 부력의 변화를 재계산하고, 불균형력의 크기가 허용 값보다 작아 질 때까지 반복적으로 계산을 수행한다.

Fig. 5.

Process of time-elapsed and lightering plan calculation.

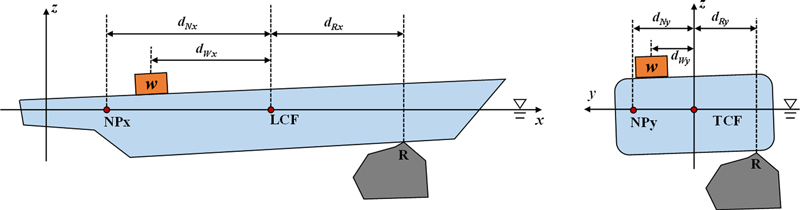
U.S. Navy [2013]에 따르면, 수심변화 및 중량 조절 작업에 따른 지반반력 변화를 아래와 같이 간략화 된 식으로 표현하였다. 수식에 나타난 거리는 Fig. 6을 통해서 의미를 살펴 볼 수 있다.

Fig. 6.

Schematic of distances for neutral, ground reaction, and additional weight points.

- 수심 변화에 따른 지반반력 변화: U.S. Navy Manual, Original

지반반력 작용점 흘수 변화량 = 선체 부상 + 종경사 영향

$\[ \begin{array}{l}-t=\frac{\delta R}{TPC}+\left(\frac{\delta R\cdot d_{Rx}}{MTC}\right)\cdot \left(\frac{d_{Rx}}{LBP}\right)\\ \Rightarrow \delta R=\frac{-t\cdot TPC\cdot MTC\cdot LBP}{\left(TPC\cdot d_{Rx}^2\right)+(MTC\cdot LBP)}\end{array} \]$

(11)

여기서 δR = 지반반력 변화량[ton]
t = 조석 간만으로 인한 지반반력 작용점 수심 변화[cm]
d_Rx = 부심(center of flotation)에서부터 지반반력 작용점까지의 x방향 거리[m]
TPC = 흘수 1 cm 증가 시 필요한 추가 배수량[ton/cm]
MTC = 종경사 1 cm 증가 시 필요한 모멘트[ton.m/cm]
LBP = 수선간 거리[m]

- 중량 조절에 따른 지반반력 변화: U.S. Navy Manual, Original

$\[ \delta R=w\times \frac{d_{Wx}-d_{Nx}}{d_{Rx}-d_{Nx}}=w\times \frac{d_{NWx}}{d_{NRx}} \]$

(12)

여기서 w = 추가 또는 제거된 중량[ton]
d_Wx = 부심에서부터 추가 or 제거된 중량까지의 x방향 거리[m]
d_Nx = 부심에서부터 중립점까지의 거리[m]$$ d_{Nx}=\frac{MTC\cdot LBP}{TPC\cdot d_{Rx}}$$
d_Rx = 부심에서부터 지반반력 작용점까지의 거리
d_NWx = 중립점에서부터 추가 or 제거된 중량까지의 거리[m]
d_NRx = 중립점에서부터 지반반력 작용점까지의 거리[m]

위의 식에서 중립점(Neutral loading point, NP)은 지반반력을 변화시키지 않고 무게를 추가하거나 제거할 수 있는 지점을 의미한다. 중립점에 화물을 추가하면 수심과 종경사가 동시에 변화한다. 수심 변화는 지반반력을 증가시키는 방향으로 작용하고, 종경사는 지반반력을 감소시키는 방향으로 작용하여, 두 가지 효과가 상쇄되면서 결과적으로 지반반력은 변화하지 않는다. 중립점과 달리 좌초점(지반반력 작용점)에 무게를 추가하거나 제거할 경우, 변화된 무게만큼 지반반력이 직접적으로 변한다. 즉, 좌초점에 화물을 추가하면 선박의 자세 변화는 일어나지 않으며, 추가된 무게에 상응하는 만큼 지반반력이 증가한다.

한 가지 언급하고자 하는 바는, 위의 식은 기존의 수식을 미터법으로 나타낸 형태이며, 선박의 몇몇 정유체력 특성 값만을 사용하여 지반반력의 변화량을 간단하게 계산할 수 있는 방법이다. 다만 등흘수(evenkeel) 상태에서 미소 변화가 있는 경우를 가정하였기 때문에 자세변화가 클수록 오차가 커질 수 있다. 또한 종경사에 의한 선수트림을 반영하였지만 횡경사에 의한 변화량을 고려하지 않았는데, 횡경사의 영향은 아래의 식과 같이 추가적으로 반영할 수 있다.

- 수심 변화에 따른 지반반력 변화: U.S. Navy Manual, Modified

지반반력 작용점 흘수 변화량 = 선체 부상 + 종경사 영향 + 횡경사 영향

$\[ \begin{array}{l}-t=\frac{\delta R}{TPC}+\left(\frac{\delta R\cdot d_{Rx}}{MTC}\right)\cdot \left(\frac{d_{Rx}}{LBP}\right)+\left(\frac{\delta R\cdot d_{Ry}}{MHC}\right)\cdot \left(\frac{d_{Ry}}{B}\right)\\ \Rightarrow \delta R=\frac{-t}{\frac{1}{TPC}+\frac{d_{Rx}^2}{MTC\cdot LBP}+\frac{d_{Ry}^2}{MHC\cdot B}}\end{array} \]$

(13)

여기서 d_Ry = 부심에서부터 지반반력 작용점까지의 y방향 거리[m]
MHC = 횡경사 1 cm 증가 시 필요한 모멘트[ton.m/cm]
B = 선박 폭[m]

- 중량 조절에 따른 지반반력 변화: U.S. Navy Manual, Modified

$\[ \delta R=w\times \frac{d_{Wx}-d_{Nx}+d_{Wy}\frac{d_{Nx}}{d_{Ny}}}{d_{Rx}-d_{Nx}+d_{Ry}\frac{d_{Nx}}{d_{Ny}}}=w\times \frac{d_{NWx}+d_{Wy}\frac{d_{Nx}}{d_{Ny}}}{d_{NRx}+d_{Ry}\frac{d_{Nx}}{d_{Ny}}} \]$

(14)

여기서 d_Wy = 부심에서부터 추가 or 제거된 중량까지의 y방향 거리[m]
d_Ny = 부심에서부터 중립점까지의 y방향 거리[m]$$ d_{Ny}=\frac{MHC\cdot B}{TPC\cdot d_{Ry}}$$

위의 수식은 종경사 1 cm당 필요한 모멘트 MHC 개념을 추가하여 횡경사의 영향을 반영한 수식이며, 횡경사의 영향을 어느 정도 반영할 수 있다. 다만 앞에서 언급한 바와 같이, 현재의 자세가 반영된 식은 아니기 때문에 횡경사와 종경사가 큰 경우에는 오차가 커 질 수 있다.

3. 다양한 조건에서의 이초력 추정

본 장에서는 해석 프로그램을 통해서 계산한 해석 예제 및 결과를 보여준다. 대상선형은 Hebert-ABS에서 개발한 상용 구난 해석 프로그램인 HECSALV의 예제 선형인 150,000톤급 탱커 선형이며, 길이 및 폭은 266 m, 48 m이다. 첫 번째 좌초 상황은 일점 좌초 상황이며, 좌초로 인해서 종경사 및 횡경사가 발생된 경우이다. 초기자세 및 사고 이후 자세는 다음과 같다.

- 좌초 전 선박 자세: d_AP= 17.60m, d_FP = 17.49 m, Heel = 0deg
- 좌초 후 선박 자세: d_AP= 17.0 m, d_FP= 15.0 m, Heel = 5deg

Table 1은 현재 개발된 기법 및 HECSALV에서 계산된 결과를 보여주고 있다. 아래의 표에서 확인할 수 있듯이, 정유체력 정보 및 지반반력 정보가 현재 계산 값 및 상용프로그램인 HECSALV 프로그램과 거의 동일하게 나타난다. 즉 현재 개발된 해석기법의 정확도가 매우 높음을 알 수 있다. 한 가지 언급하고자 하는 바는 선박의 무게를 나타내는 “Weight”의 경우, 좌초 전 선박의 연료유를 포함한 전체 화물량의 값을 확인하여 입력 값으로 사용할 수 있으며, 또는 좌초 전 선박의 자세를 활용하여 배수량을 계산한 후 이를 선박의 무게로 사용할 수 있다. 본 연구에서는 두 번째 방법을 사용하여 선박의 무게를 추정하였다.

Table 1.

Comparison of calculation results

이초력을 계산하는 순서는 다음과 같다. 먼저, 좌초 직전의 자세를 사용하여 배수량을 계산하고 이를 선박의 무게로 설정한다. 그 다음, 좌초 직후의 자세를 기반으로 부력과 부력중심을 계산한다. 이후, 선박의 무게와 부력의 차이만큼을 지반반력의 크기로 가정하며, 지반반력의 위치는 모멘트 평형방정식인 Eq. (2)를 이용하여 계산한다.

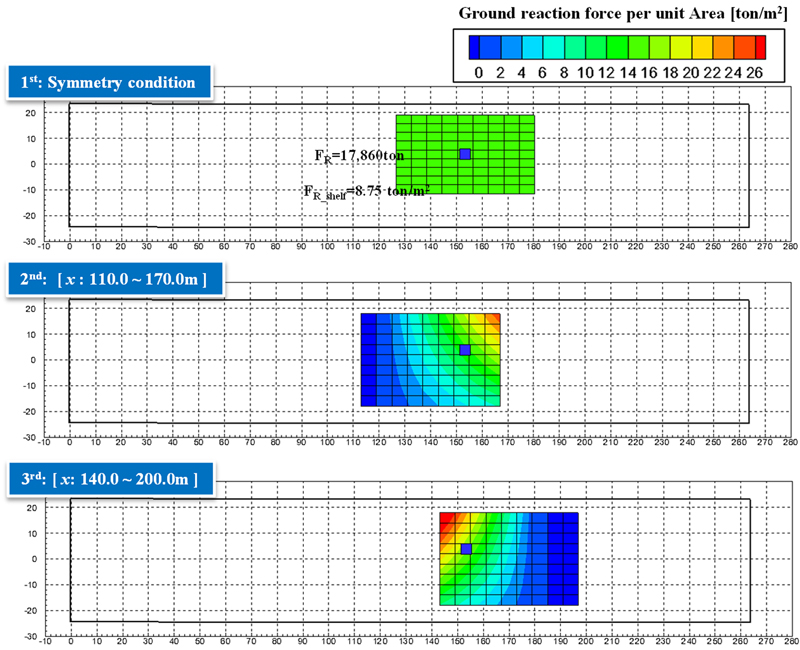
두 번째 좌초 상황은 평평한 지반에 좌초된 상황이며, 좌초 전후의 선박의 자세는 이전 계산과 동일하다. 평평한 지반영역의 크기 및 위치를 달리하여 세 번의 계산을 수행하였다. 첫 번째 계산은 평평한 지반영역이 지반반력 작용점 기준으로 좌우 대칭인 경우이며, x방향의 길이는 60 m, y방향의 길이는 34 m이다. 두 번째, 세 번째 계산의 경우 평평한 지반영역은 y방향으로는 –20 m에서 +20 m까지 길이 40m이며, x방향으로의 길이는 60m로 고정되지만 위치를 달리하며 계산하였다. Fig. 8과 같이 평평한 지반영역의 크기 및 위치에 따라서 단위면적 당 지반반력의 분포가 달라진다.

Fig. 7.

Plan views of ship’s attitude before and after grounding.

Fig. 8.

Distribution of ground reaction force according to simple shelf area.

첫 번째 계산과 같이 일점 좌초 지점 기준으로 평평한 지반 영역이 대칭인 경우 영역 전체에서 지반반력이 동일하게 분포되며, 단위면적당 지반반력의 크기는 일점 좌초 시 지반반력의 크기를 평평한 지반 영역의 전체 면적으로 나눈 값이 된다. 영역이 비대칭인 경우 일점 좌초 지점과 가까운 부분에서 더 큰 지반반력이 발생하며, 평평한 지반영역이 일점 좌초 지점으로 치우칠수록, 단위면적당 지반반력의 최대값은 커진다.

4. 모형시험을 통한 프로그램 검증

4.1 모형시험 준비

모형시험은 선박해양플랜트연구소 심해공학수조(부산)에서 수행하였으며, Fig. 9는 심해공학수조 내부 전경을 보여주고 있다. 심해공학수조는 100 m × 50 m × 15 m(심해 피트 50 m) 규모이며, 수심조절판을 사용하여 깊이 전 구간에서 수심조절이 가능하다. 파도, 조류, 바람 발생장치를 활용하여 실제 해상환경을 모사할 수 있다(Korea Research Institute of Ships & Ocean Engineering [2024]).

Fig. 9.

Interior overview of Deep Ocean Engineering Basin (DOEB).

현재 이초력 모형시험은 Fig. 10과 같이 심해공학수조의 준비수조에서 진행하였다. 준비수조의 크기는 10 m × 3.3 m × 2.0 m 이며, 유압식 리프트를 사용하여 선박의 수심을 조절할 수 있다.

Fig. 10.

Preparation tank and hydraulic lift of Deep Ocean Engineering Basin.

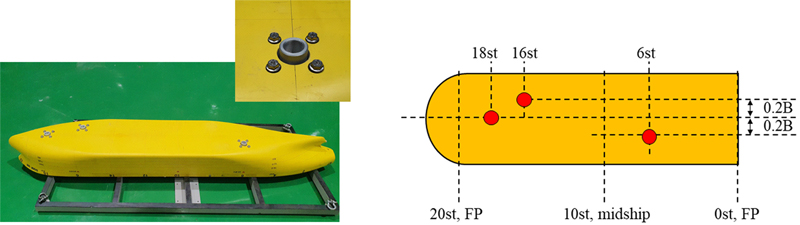
모형시험 대상선박은 국내 해양사고 건수 통계를 참고하여 국내 해안에서 사고가 빈번하게 일어나는 100 m급 small tanker로 결정하였다. 다만 이에 해당하는 가용할 수 있는 선박이 없었으며, 따라서 KRISO 공시선형인 KVLCC2 선형을 100급으로 축소하여 사용하였다. 모형선의 크기는 축적비 1/50인 2 m로 결정하였으며, 주요 제원은 Table 2와 같다.

Table 2.

Principle dimensions of test model

Fig. 11은 2 m 모형선을 제작하여 최종 세팅한 사진이며, 목표치에 맞도록 무게 추를 분포시켰다. 선박의 GM_T, Iyy, T_roll의 오차 값이 2% 이내이며, 모형선에는 프로펠러와 러더가 포함되어 있다.

Fig. 11.

Photos of model ship setup.

좌초 상황은 일점 좌초된 상황만을 가정하였으며, 좌초 위치는 Fig. 12와 같이 3가지 다른 위치(18st, 16st, 6st)로 설정하였다. 18st의 좌초 지점은 선박 센터라인에 위치하며, 16st는 좌현으로 0.2B, 6st는 우현으로 0.2B 만큼 틀어진 상태로 좌초 지점이 위치한다. 각 좌초 지점은 계측 센서와 연결되어야 하기 때문에 사전에 선박 바닥면 수정이 필요하며, 아래의 그림과 같이 바닥면 연결 지그를 추가하는 수정작업을 진행하였다.

Fig. 12.

Grounding position and adjustment of model ship bottom.

좌초선의 지반반력을 계측하기 위해서 Fig. 13과 같이 완전 방수형 로드셀을 제작하여 지반반력을 계측하였으며, 방수형 로드셀을 선체와 바닥 사이에 연결해 줄 수 있는 바닥판 및 치구를 제작하여 모형시험에 사용하였다. 선박의 자세는 광학계측시스템을 사용하여 계측하였으며, 준비수조의 리프트 높낮이를 변화시켜가면서 지반 반력 작용점의 수심을 조절하였다. 준비수조에서의 시험을 통해서 좌초위치, 수심 및 중량 조절에 따른 선박의 자세 및 지반반력을 계측하였다. 아래의 그림은 준비수조에서 이초력 시험을 위해서 선박을 세팅하였을 때의 모습이다.

Fig. 13.

Setup freeing force test in the preparation tank.

4.2 모형시험 결과

앞서 언급한 바와 같이, 모형시험에서 다루는 좌초 상황은 선박이 특정한 한 지점에 좌초된 경우이며, 좌초 위치를 바꿔가면서(18st, 16st, 6st, Fig. 12 참고) 시험을 진행하였다. 모형시험은 이초 해석법의 검증을 위해 실제 해석 과정과 동일한 3단계로 구성하였다. 첫 번째 단계는 초기 좌초 계산으로, 이 단계에서는 좌초 위치에따른 선박의 자세 및 지반반력을 측정하였다. 측정된 결과는 현재 개발된 이초력 계산법의 결과와 비교하여 그 정확성을 평가하였다. 두 번째 단계는 수심 변화에 따른 계산으로, 이는 조석 변화나 기타 환경적 요인에 의해 수심이 변화할 때 선박에 미치는 영향을 분석하기 위한 것이다. 이 단계에서는 준비수조의 리프트를 활용하여 지반 반력 작용점의 수심을 조절하면서 선박의 자세 및 지반 반력을 측정하였다. 세 번째 단계는 중량 조절 작업 계산 단계이다. 이 단계에서는 추가적인 중량 조절 작업이 선박의 자세와 지반 반력에 미치는 영향을 평가하기 위해 4 kg의 무게를 특정 위치에 추가하여 실험을 수행하였다. 두 번째 및 세 번째 단계에서는 기존의 Salvage Manual (U.S. Navy [2013])에서 제시된 원본식과, 횡경사를 고려하여 수정된 식을 활용하여 추가적인 비교 분석을 수행하였다. 이를 통해 새로운 해석 기법이 기존의 공식들과 어떻게 차별화되는지, 그리고 보다 정확한 해석을 위해 어떤 부분에서 개선이 이루어졌는지를 확인하였다.

4.2.1 초기 좌초 계산

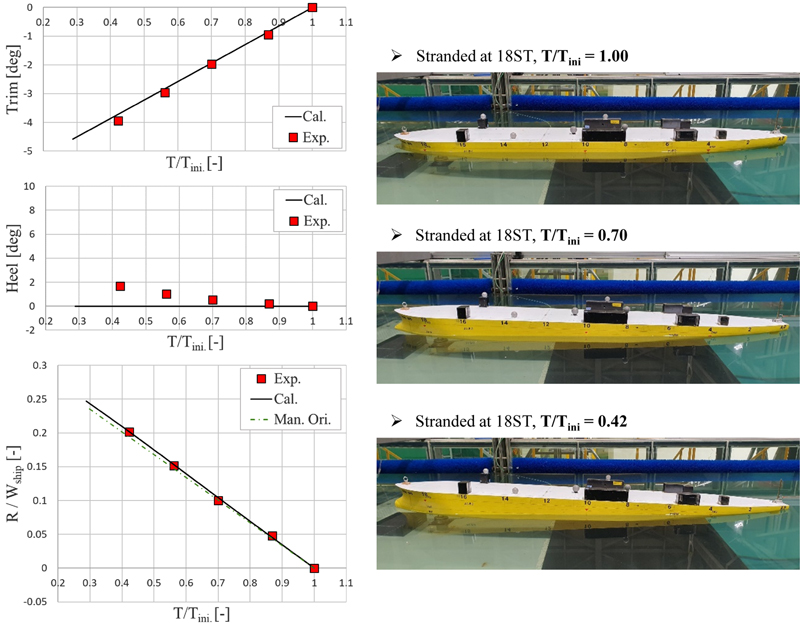
초기 좌초 계산 단계에서는 선박이 특정한 한 지점에 좌초된 경우를 다루었으며, 좌초 위치를 18st, 16st, 6st으로 변경해 가면서 결과를 비교하였다. 먼저 18st에서 좌초된 결과(Table 3 & Fig. 14)를 살펴보면, 수치해석에서의 선박의 자세(선수 선미에서의 흘수, 종경사, 횡경사)와 지반반력의 크기가 모형시험과 거의 동일하며, 지반반력에서의 오차가 가장 큰 편이지만 그마저도 2.5% 이내인 것을 확인하였다. 다만 한가지 언급하고자 하는 바는 첫 번째 좌초 위치는 y방향으로 센터라인에 위치하기 때문에 이상적으로는 횡경사가 발생하지 않아야 했지만, 모형시험의 불확실성으로 인해서 완벽한 대칭이 되지 않아서 횡경사가 0.5deg 정도 발생하였다. 하지만 이는 그렇게 크지 않은 각도이며, 무시할 만한 수준이라고 판단된다.

Table 3.

Comparison of ship attitude and ground reaction force: grounded at 18st

Fig. 14.

Ship attitude in model test and numerical analysis: grounded at 18st.

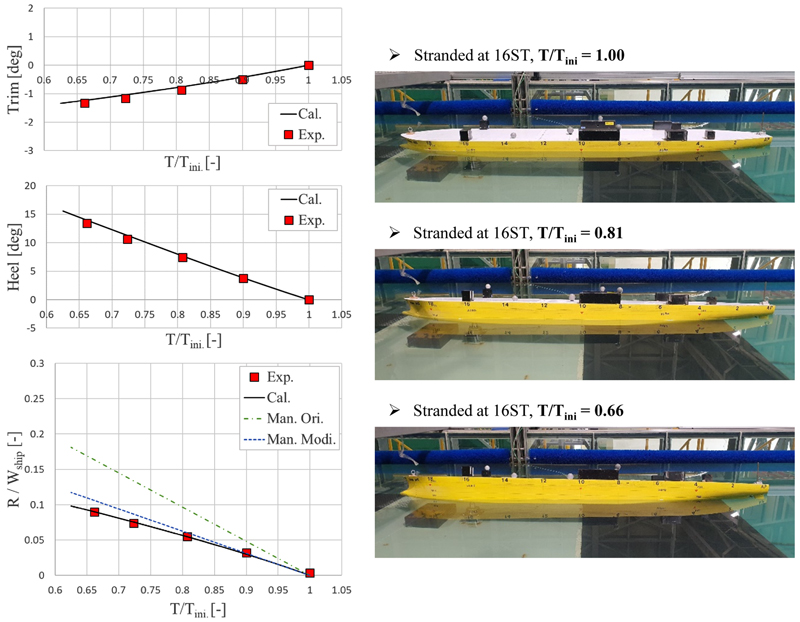
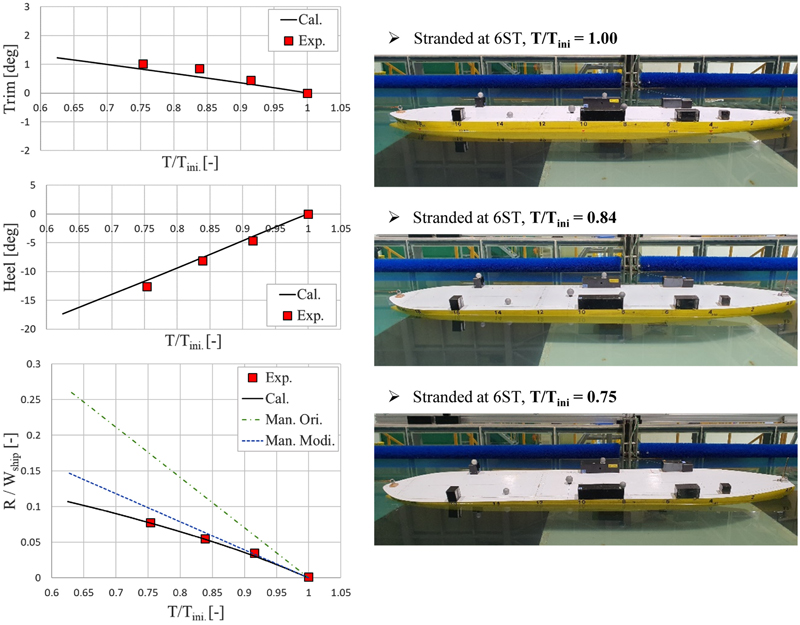
다음으로 16st에서 좌초된 결과(Table 4 & Fig. 15)와 6st에서 좌초된 결과(Table 5 & Fig. 16)를 살펴보면, 좌초 위치가 센터라인에서 벗어난 곳에 위치하여 10deg 이상의 큰 횡경사가 발생하였다. 첫 번째 케이스에 비해 수치해석으로 계산한 선박의 자세에서 오차가 다소 크게 발생하였으며, 특히 6st 좌초의 경우 종경사 오차율이 약 17%정도로 큰 편이다. 그러나 종경사 및 오차의 절대적인 값은 1deg, 0.17deg로 작으며, 이는 모형시험 시의 계측 오차도 어느 정도 포함된 것으로 보인다. 지반반력의 경우 세 가지 모두에서 오차율이 2.5% 이내로 매우 정확하게 추정하고 있으며, 선박의 자세 변화가 큰 경우에도 현재의 이초력 해석 기법이 높은 정확성을 유지함을 확인하였다.

Table 4.

Comparison of ship attitude and ground reaction force: grounded at 16st

Table 5.

Comparison of ship attitude and ground reaction force: grounded at 6st

Fig. 15.

Ship attitude in model test and numerical analysis: grounded at 16st.

Fig. 16.

Ship attitude in model test and numerical analysis: grounded at 6st.

4.2.2 수심 변화에 따른 결과

다음으로 수심 변화에 따른 결과를 살펴본다. Fig. 17~19은 각각 18st, 16st, 6st 지점에서의 좌초상황을 나타내며, 각 좌초 지점에서 수심이 변화함에 따라 선박의 자세 및 지반반력의 변화를 계측한 결과를 보여준다. 각 그래프에서 x축의 T는 지반반력 작용점의 현재 흘수를 의미하며, T_ini.는 좌초되기 이전의 흘수를 의미한다. 따라서, T/T_ini. = 1.0은 좌초 이전의 등흘수 상태를 나타내며, 이 경우 종경사, 횡경사 및 지반반력은 모두 0이 된다. 조석간만으로 인해 수심이 얕아지면서 T/T_ini.가 줄어들며, 종경사, 횡경사 및 지반반력의 크기는 증가한다. 아래의 지반반력 그래프에서 지반반력의 크기는 선박의 무게로 무차원화 하여 나타내었으며, 총 4개의 결과가 포함되어 있다. 빨간색 점은 모형시험을 통해서 계측한 결과이며, 검정색 선은 현재 개발된 이초력 해석 기법으로 계산된 결과이다. 초록색 파선은 Salvage manual (U.S. Navy [2013])의 원본 식(Eq. 11)을 사용한 결과이며, 파란색 파선은 이 원본 식에서 횡경사의 영향을 반영하여 수정한 식 (Eq. 13)의 결과이다.

Fig. 17.

Comparison of attitude and ground reaction by water depth: grounded at 18st.

Fig. 18.

Comparison of attitude and ground reaction by water depth: grounded at 16st.

Fig. 19.

Comparison of attitude and ground reaction by water depth: grounded at 6st.

먼저, 18st 지점에서의 좌초 결과(Fig. 17)를 보면, 수심이 얕아짐에 따라서 종경사와 지반반력의 크기가 커지는 경향이 관찰되며, 현재 개발한 이초력 계산 기법의 결과가 모형시험 결과와 잘 일치하는 것을 확인할 수 있다. 이 경우는 횡경사가 발생하지 않으므로, Eq. 11의 원본 식이 지반반력을 높은 정도로 추정함을 알 수 있다. 다음으로, 16st 및 6st 지점에서의 좌초 결과(Fig. 18, 19)를 살펴보면, 좌초 위치가 센터라인에서 벗어난 지점이기 때문에 수심이 얕아짐에 따라서 횡경사의 크기가 급격하게 증가하는 것을 확인할 수 있다. 이 경우, 수치해석으로 계산한 선박의 자세 및 지반반력의 크기는 모형시험의 결과를 잘 따라가는 것(평균 오차율 2.8%)을 알 수 있다. 그러나 Eq. 11의 원본 식을 사용하여 계산한 지반반력은 과도하게 추정되는 경향(평균 오차율 85.6%)이 있다. 실제 상황에서는 좌초 위치가 센터라인에서 벗어나 있음에 따라 횡경사가 발생하면서 손실되는 부력의 크기가 감소하지만, 원본 식에서는 이를 반영하지 못하여 지반반력이 과도하게 추정된다. 횡경사를 반영한 수정식(Eq. 13)을 사용한 계산 결과는 원본 식보다 결과가 상당히 많이 개선(오차율 11.3%)되는 것을 확인하였다. 하지만 여전히 선박의 횡경사가 큰 경우에는 모형시험과 오차가 있으며, 실제보다 큰 값을 추정하는 경향이 있다. 앞서 언급한 바와 같이 이러한 오차는 Salvage manual (U.S. Navy [2013])의 식이 선박의 현재 자세를 반영하지 않기 때문에 발생한다. 그럼에도 불구하고 이 식은 매우 유용한데, 사고 전 선박의 정유체력 특성 값 몇 가지만으로도 변화하는 지반 반력을 일정 수준의 정확도로 계산할 수 있기 때문이다.

4.2.3 중량조절 작업 결과

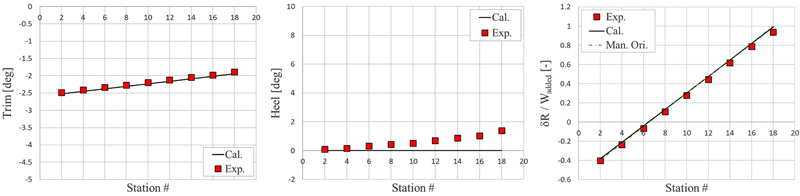
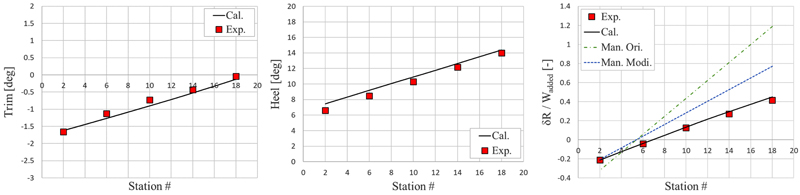
마지막으로 중량조절 작업에 따른 결과를 살펴본다. 이를 위해, 좌초 위치가 18st와 16st의 특정 초기 수심에서 4 kg의 무게 추를 추가하여 선박의 자세 및 지반반력을 계측하였다. 무게 추를 추가하는 위치는 모형선 갑판 상부의 센터라인이며, 이 위치를 길이 방향으로 18st에서 2st까지 이동시키면서 변화를 살펴보았다. Fig. 20, 21에서 x축은 무게 추가 추가된 선박의 스테이션 번호를 나타낸다. 지반반력 그래프에서는 지반반력의 크기를 추가된 무게로 나누어서 무차원화 된 값으로 표현했으며, 총 4개의 결과가 포함되어 있다. 빨간색 점은 모형시험을 통해서 계측한 결과이며, 검정색 선은 현재 개발된 이초력 해석 기법으로 계산한 결과이다. 초록색 파선은 Salvage manual(U.S. Navy [2013])의 원본 식 (Eq. 12)을 사용한 결과이며, 파란색 파선은 원본 식에서 횡경사의 영향을 포함하여 수정한 식 (Eq. 14)을 적용한 결과이다.

Fig. 20.

Comparison of attitude and ground reaction with added weight: grounded at 18st, T/Tini. = 0.7.

Fig. 21.

Comparison of attitude and ground reaction with added weight: grounded at 16st, T/Tini. = 0.792.

먼저 Fig. 20을 살펴보면, 선박의 좌초 위치는 18st 센터라인이며, 초기 수심은 T/T_ini. = 0.7로 설정하였다. 4 kg의 무게 추를 추가한 후, 그 위치를 변경하면서 선박의 종경사, 횡경사 및 지반반력을 측정하고 계산 결과와 비교하였다. 이 경우 횡경사가 발생하지 않아, 모형시험 결과와 수치해석 결과, Salvage manual(U.S. Navy [2013])의 원본 식의 결과 모두 잘 일치하는 것을 확인 할 수 있다. 특히, 지반반력의 작용점에 무게를 추가하면 추가한 무게만큼 지반반력이 증가하는 점(δR/W_added= 1 at x = 18st)과 중립점(x = 6.55st)에 무게를 추가하였을 때 지반반력의 변화가 없는 점도 일치한다.

다음으로 Fig. 21을 살펴보면, 선박의 좌초 위치는 16st 좌현(y = 0.2B)이며, 초기 수심은 T/T_ini. = 0.792이다. 현재 개발한 이초력 해석 기법으로 계산한 결과는 모형시험과 잘 일치(평균 오차율 2.9%)하는 반면, Eq. 12의 원본 식을 사용한 경우 다소 큰 오차(평균 오차율 89.4%)가 발생하는 것을 알 수 있다. 이는 실제 현상에서는 좌초 위치가 센터 라인에서 벗어나 있어 횡경사가 발생하면서 손실되는 부력의 크기가 줄어드는데, 원본 식에서는 이를 반영하지 않았기 때문이다. 횡경사 발생에 따른 영향을 반영한 수정 식(Eq. 14)를 적용하면 이러한 오차가 줄어들지만(평균 오차율 11.6%), 횡경사가 크게 발생한 경우에는 오차가 여전히 크게 발생할 수 있다. 또한, Fig. 21에서 중립점의 위치가 Salvage manual에서 추정한 값(d_Nx, Eq.12 참고)과 차이를 보이는 것도 이 식이 현재 선박의 자세를 반영하지 않았기 때문으로 생각된다.

5. 결 론

본 연구에서는 좌초된 선박의 이초력 추정 기법을 개발하였으며, 이를 바탕으로 다양한 좌초 조건에서의 이초력 추정 방법을 정의하고 검증하였다. 연구 과정에서 대표적인 참고문헌인 Salvage Manual (U.S. Navy[2013])을 분석하였으며, 횡경사 영향을 보완한 지반반력 추정식을 제안하였다. 또한, 개발된 기법의 검증을 위해 선박해양플랜트연구소 심해공학수조에서 모형시험을 수행하였으며, 개발된 기법과의 비교를 통해서 정확도를 확인하였다. 이 연구를 통해 얻은 주요 결론은 다음과 같다.

- 정유체력 데이터를 활용한 이초력 추정 기법 개발: 배수량 표(Hydrostatic table), 본진 표(Bonjean table), 복원력 교차곡선 표(cross-curve table)와 같은 정유체력 데이터를 활용하여 좌초 선박의 이초력을 정확히 추정할 수 있는 기법을 개발하였다. 상용 프로그램인 HECSALV와의 결과 비교를 통해, 개발된 프로그램이 유사한 결과를 도출함을 확인하였다.

- 다양한 좌초 조건에서의 이초력 추정 방법 정의: 본 연구는 일점 좌초뿐만 아니라 다양한 좌초 조건에서의 이초력 추정 방법을 정의하였다. 특히, 평평한 지반의 영역에 따른 결과 변화를 확인하여, 좌초 조건에 따라 달라지는 이초력의 변화를 체계적으로 분석하였다.

- Salvage manual의 원본 식 개선: 원본 식에서 횡경사에 의한 영향을 반영한 수정 식을 제안하였으며, 이를 통해 횡경사가 존재하는 경우에도 간단한 정유체력 데이터를 활용하여 보다 정확한 이초력 추정이 가능함을 확인하였다.

- 모형시험을 통한 검증 데이터 구축 및 이초력 추정 기법 검증: 심해공학수조에서 진행한 모형시험을 통해, 좌초 위치, 수심 변화, 중량 이동 등에 따른 선박의 자세 및 지반반력을 계측하였으며, 검증 데이터를 구축하였다. 이러한 데이터를 바탕으로 개발된 이초력 추정 기법의 결과와 비교 검증을 수행하였으며, 개발된 기법이 다양한 좌초 상황에서도 높은 정확도를 유지함을 확인하였다.

본 연구에서 개발된 이초력 추정 기법은 다양한 좌초 상황에서 신뢰성 있는 이초력 추정을 가능하게 하며, 실무에서의 적용 가능성을 높인다. 이 연구를 통해 얻은 결과는 해양 구조 작업의 효율성을 증대시키는 데 중요한 기여를 할 것으로 기대된다.

Acknowledgments

본 논문은 해양경찰청 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구입니다(해양오염방지 긴급구난 의사결정 지원기술 개발, PMS5660).

References

• Bennett, S.S. and Phillips, A.B., 2017, Experimental investigation of the influence of floodwater due to ship grounding on motions and global loads. Ocean Engineering 130, 49-63. [https://doi.org/10.1016/j.oceaneng.2016.11.039]
• Herbert-ABS, HECSALV, https://www.herbert-abs.comhecsalv, , 2024 (accessed 2024.09.09).
• Hussein, A.W., El-Dessouky, U.M., El-Kilani, H.S. and Hegazy, E.H., 2016, Grounding contingency plan for intact double hull tanker. Alexandria Engineering Journal 55, 235-241. [https://doi.org/10.1016/j.aej.2015.10.017]
• Korea Research Institute of Ship & Ocean Engineering, Deep Ocean Engineering Research Center, https://www.kriso.re.kr/menu.es?mid=a10208030000, , 2024 (accessed 2024.08.30).
• Lee, W., Ham, S.-H. and Ku, N., 2022, A Calculation Method of the Ship’s Posture Based on the Static Equilibrium for the Refloating Plan of the Stranded Ship. SNAK 59, 55-63. [https://doi.org/10.3744/SNAK.2022.59.1.55]
• Mazaheri, A., Montewka, J. and Kujala, P., 2016, Towards an evidence-based probabilistic risk model for ship-grounding accidents. Safety Science 86, 195-210. [https://doi.org/10.1016/j.ssci.2016.03.002]
• Pineau, J.-P., Conti, F., Le Sourne, H. and Looten, T., 2022, A fast simulation tool for ship grounding damage analysis. Ocean Engineering 262, 112248. [https://doi.org/10.1016/j.oceaneng.2022.112248]
• Pineau, J.-P. and Le Sourne, H., 2023, Analytical modelling of ship bottom grounding considering combined surge and heave motions. Marine Structures 88, 103364. [https://doi.org/10.1016/j.marstruc.2022.103364]
• Simonsen, B.C., 1997, Ship grounding on rock—I. Theory. Marine Structures 10, 519-562. [https://doi.org/10.1016/S0951-8339(98)00002-1]
• Simonsen, B.C., 1997, Ship grounding on rock—II. Validation and application. Marine Structures 10, 563-584. [https://doi.org/10.1016/S0951-8339(98)00003-3]
• Navy, U.S., 2013, Salvage Manual Volume 1: Strandings, Harbor Clearance, and Afloat Salvage, Naval Sea Systems Command,
• Youssef, S.A.M. and Paik, J.K., 2018, Hazard identification and scenario selection of ship grounding accidents. Ocean Engineering 153, 242-255. [https://doi.org/10.1016/j.oceaneng.2018.01.110]
• Zhu, L., Zhou, Z. and Pedersen, P.T., 2024, Ship grounding model tests in a water tank: An experimental study. Marine Structures 93, 103529. [https://doi.org/10.1016/j.marstruc.2023.103529]
• Varsami, A., 2014, Different Methods of Refloating a Ship. Advanced Materials Research 837, 792-797. [https://doi.org/10.4028/www.scientific.net/AMR.837.792]